
- •К практическому занятию № Пример алгоритма декомпозиции. Реализация и сложность алгоритма а.А.Карацубы
- •Оценка эффективности алгоритма
- •К практическому занятию № Деревья. Обход дерева. Бинарные деревья.
- •К практическому занятию № Модели внутренней сортировки.
- •К практическому занятию № Алгоритм быстрой сортировки quicksort.
К практическому занятию № Пример алгоритма декомпозиции. Реализация и сложность алгоритма а.А.Карацубы
Алгоритм А.А.Карацубы позволяет сводить умножение двух n-значных чисел к трем умножениям n/2-значных чисел и нескольким операциям «+», «- » и разрядного сдвига.
Разрядный
сдвиг
для
чисел, записанных в g-ичной
системе счисления (g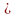 ℕ,
g>1)-умножение
или деление числа на степень g.
Приводит к перемещению разрядной точки,
приписыванию или отбрасыванию нулей.
Разрядный сдвиг является менее затратной
операцией по сравнению с умножением
(делением) на произвольное число.
ℕ,
g>1)-умножение
или деление числа на степень g.
Приводит к перемещению разрядной точки,
приписыванию или отбрасыванию нулей.
Разрядный сдвиг является менее затратной
операцией по сравнению с умножением
(делением) на произвольное число.
Пусть даны два n-значных числа, записанных в g-ичной системе счисления (g ℕ, g>1)
A=a a
a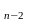
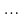 a
a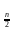 a
a a
a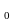 (g),
B=b
b
b
b
b
(g)
(g),
B=b
b
b
b
b
(g)
Т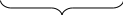
 огда
A=(a
g
огда
A=(a
g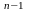 +a
g
+a
g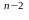 +
+a
g
+
+a
g )+
a
g
)+
a
g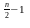 +
+
a
=
g
(a
g
+
+
a
=
g
(a
g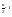 +a
g
+a
g +
+a
)+
a
g
+
a
+
+a
)+
a
g
+
a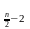 g
g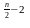 +
+
a
=
g
A1+A0,
где
+
+
a
=
g
A1+A0,
где
A1
A0
A1=a a a (g), A0=a a a (g)
Аналогично, B= g B1+B0, где B1=b b b (g) , B0=b b b (g)
Рассмотрим
AB=( g
A1+A0)(g
B1+B0)=A1B1g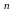 +(A1B0+A0B1)
g
+
A0B0
(1)
+(A1B0+A0B1)
g
+
A0B0
(1)

где С=A1B0+A0B1=(A1-A0)(B0-B1)+A1B1+A0B0 (2)
Вычисление
A∙B
по формулам (1) и (2) требует:
Трех операций уможения
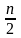 -значных
чисел A1B1,
A0B0,
(A1-A0)(B0-B1);
-значных
чисел A1B1,
A0B0,
(A1-A0)(B0-B1);Шести операций «+» и «-»;
Двух операций разрядного сдвига – умножения на∙g и ∙g .
Оценка эффективности алгоритма
Пусть T(n) - время работы алгоритма при умножении n-значных чисел A и B. (исходная задача размера n).
Количество подзадач a=3. Размер подзадачи n/2, отсюда b=2.
T(n/2) - время работы над одной подзадачей - умножением двух n/2 - значных чисел.
T(1) – время умножения двух однозначных чисел. Можем считать T(1)=c.
d(n) – время «сборки» затрачиваемое на «+», «-» и разрядный сдвиг в формулах (1) и (2).
Количество
цифр в числах A1B1,
A0B0
и (A1-A0)(B0-B1)
равно n-1.
Действительно,
например, А1В1=(a
g
+a
g
+
+a
)
(b
g
+b
g
+
+b
)=
a
b
g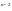 +
+a
b
,
следовательно, их сложение и вычитание
требует O(n-2)=О(n)k∙n
времени, k=const.
+
+a
b
,
следовательно, их сложение и вычитание
требует O(n-2)=О(n)k∙n
времени, k=const.
Разрядный сдвиг на n и позиции требует O(n) времени.
Итого d(n)k1n+k2n=(k1+k2)n=kn, k=const
Таким образом, рекуррентное соотношение, оценивающее временную сложность алгоритма А.А. Карацубы имеет вид
 .
(1)
.
(1)
Упражнение: Определить в терминах О-большое асимптотическую временную сложность алгоритма Карацубы для умножения двух n-значных чисел.
К практическому занятию № Деревья. Обход дерева. Бинарные деревья.
Определение 1: Дерево (ориентированное), ордерево – множество элементов - узлов, один из которых называется корнем, и отношений, образующих иерархическую структуру узлов по правилам:
Пустое множество узлов является деревом.
Один узел является деревом, он является корнем этого дерева.
Пусть n - узел, а Т1, Т2, …,Тk - деревья, с корнями n1, n2,…nk. Если n находится в отношении с n1, n2,…,nk (n – родитель узлов n1, n2,…,nk, n1, n2,…,nk – сыновья узла n), полученное множество Т с корнем n и поддеревьями Т1, Т2, …,Тk также является деревом. Сыновья одного узла называются братьями.
Определение 2. Ордерево Т={{n}, T1, …, Tk} называется упорядоченным ордеревом, если фиксирован порядок поддеревьев Т1, Т2,..., Тk. В противном случае Т называется неупорядоченным ордеревом.
В упорядоченном ордереве поддеревья Т1,…,Тk изображаются в порядке следования слева направо, сыновья – ниже родителей. Считается, что все узлы поддерева Тi-1 лежат левее любого узла поддерева Тi.
Определение
3.
Путем
из узла n1
в узел ns
называется последовательность улов
n1,
n2,
…, ns,
где ni
является родителем узла ni+1,
 .
Длиной
пути
n1,
n2,
…, ns
называется
число s-1.
Следовательно, путь
длины 0
- это путь от n1
к n1
(к самому себе). Если существует путь от
узла
.
Длиной
пути
n1,
n2,
…, ns
называется
число s-1.
Следовательно, путь
длины 0
- это путь от n1
к n1
(к самому себе). Если существует путь от
узла
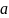 к узлу
к узлу
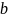 ,
то
называется предком
узла
,
а
- потомком
узла
.
,
то
называется предком
узла
,
а
- потомком
узла
.
Если путь от a к b имеет длину > 0, то называется истинным предком , а называется истинным потомком .
Узел, не имеющий истинных потомков, называется листом дерева.
Высотой узла дерева называется длина самого длинного пути из этого узла, до какого-нибудь, листа дерева. Высотой дерева называется высота его корня. Глубиной узла называется длина пути (он единственный) от корня до этого узла.
Обход дерева – упорядочение всех узлов дерева по некоторому правилу.
Рассмотрим правила обхода дерева в прямом, обратном и симметричном порядке.
Если Т - дерево, состоящее из одного узла n, в список узлов заносится этот узел.
Если Т - дерево с корнем n и поддеревьями Т1, Т2, …, Тk, то:
При обходе в прямом порядке (прямом обходе) сначала посещается (заносится в список) корень n, затем осуществляется обход в прямом порядке всех узлов Т1, затем Т2,...Тk.
При обходе в обратном порядке (обратном обходе) сначала посещаются в обратном порядке все узлы Т1, затем посещаются поддеревья Т2,…Тk, также в обратном порядке. Последним посещается корень n.
При симметричном обходе сначала осуществляется симметричный обход всех узлов Т1, далее корень n, далее в симметричном порядке узлы Т2, Т3,..., Тk.
Определение 4. Бинарное (двоичное) дерево – множество элементов - узлов, один из которых называется корнем, и отношений, образующих иерархическую структуру узлов по правилам:
Пустое множество узлов является бинарным деревом.
Один узел является бинарным деревом, он же является корнем этого дерева.
Пусть n - узел, а Т1, Т2 – бинарные деревья, с корнями n1, n2. Если n находится в отношении с n1, n2 (n – родитель узлов n1, n2, n1, n2 – сыновья узла n, причен n1 определен как левый сын n, а n2 определен как правый сын n), полученное множество Т с корнем n и бинарными поддеревьями Т1, Т2 также является бинарным деревом.
Замечание 1. В бинарном дереве, по определению 4, одно из бинарных поддеревьев Т1, Т2, или оба поддерева, могут быть пустыми бинарными деревьями. То есть узел n может иметь только левого сына n1, или только правого сына n2, или не иметь сыновей.
Замечание 2. Бинарное дерево не является упорядоченным ордеревом. Если в упорядоченном ордереве узел n имеет единственного сына n’, то узел n’ не может быть определен как левый или правый.
Пример.
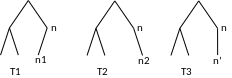
Деревья Т1 и Т2 как бинарные деревья различны, так как Т1 имеет только левого сына n1, Т2 имеет только правого сына n2. Если же рассматривать Т1 и Т2 как упорядоченные ордеревья в смысле определения 1, то они совпадают и могут быть изображены как Т3.
П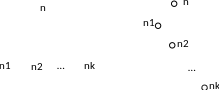 редставление
упорядоченных ордеревьев бинарными
деревьями:
от узла n
ордерева проводится левая
связь к самому левому сыну
n1,
а от n1
– правая
связь к правому брату
n2
и т.д.
редставление
упорядоченных ордеревьев бинарными
деревьями:
от узла n
ордерева проводится левая
связь к самому левому сыну
n1,
а от n1
– правая
связь к правому брату
n2
и т.д.
