
- •Математические методы теории оптимизации. Понятие экстремальных задач, примеры. Основные понятия лп.
- •Историческая справка.
- •Задача планирования производства.
- •Задача о рационе.
- •Транспортная задача.
- •Раздел 1. Линейное программирование.
- •Определение канонической формы задач.
- •Основные свойства решения задач лп
- •Элементы выпуклого анализа.
- •Множество решений задачи линейного программирования (если оно не пусто) является выпуклым многогранником.
- •Любая точка многогранника решений является линейно - выпуклой комбинацией его угловых точек. Опорное и базисное решение.
- •Алгебраическая характеристика угловой точки.
- •Симплексный метод.
- •Задача № 1.
- •Правило определения вектора вводимого в базис.
- •Метод искусственного базиса (м-метод).
- •Расширенная задача.
- •Исходная симплекс-таблица расширенной задачи.
- •Теория двойственности в линейном программировании.
- •Экономическая интерпретация
- •Виды моделей двойственных задач.
- •Соответствие между прямой и двойственной задачами.
- •Нахождение решения двойственной задачи по симплекс-таблице оптимального решения прямой задачи.
- •Экономическая интерпретация двойственности.
- •Экономическая интерпретация переменных двойственных задач.
- •Раздел II. Специальные задачи лп Целочисленное программирование.
- •Задачи целочисленного программирования.
- •Пример: «Задача о рюкзаке (задача загрузки корабля)»
- •Пример: «Задача о распределение инвестиций»
- •Первый алгоритм Гомори (аддитивный)
- •Алгоритм Гомори состоит из двух шагов:
- •Метод ветвей и границ.
- •Специальные виды целочисленных задач. Транспортная задача
- •Методы решения транспортной задачи
- •Вторая транспортная теорема
- •Метод потенциалов (Канторович)
- •Алгоритм решения
- •Задача о назначениях. Венгерский алгоритм.
- •А лгоритм решения:
Пример: «Задача о распределение инвестиций»
И меется
n
проектов и для любого j-ого
проекта определен эффект от реализации
γj
при
необходимых объемах инвестиций gj,
т.е. γj
gj.
меется
n
проектов и для любого j-ого
проекта определен эффект от реализации
γj
при
необходимых объемах инвестиций gj,
т.е. γj
gj.
Общий объем инвестиций не превышает В. Определить, какие проекты нужно реализовать, чтобы суммарный эффект был максимальным.
Х = 0 если Рj не реализуется
если Рj реализуется
Тогда
![]() при
ограничениях
при
ограничениях
![]()
Первый алгоритм Гомори (аддитивный)
Идея: задача решается симплекс-методом «с ослабленными ограничениями» (без условия целочисленности на переменные). Затем подбирается дополнительное линейное ограничение, обеспечивающее за конечное число шагов получение оптимального целочисленного решения или установление факта его отсутствия.
Г
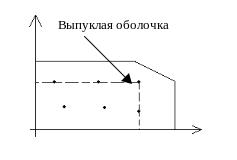
В выпуклой оболочке все угловые точки
имеют только целочисленные координаты,
но из-за трудности ее построения оболочки
строится «промежуточный» многогранник,
охватывающий всю целостную оболочку;
полностью содержащийся в области
допустимых решений, угловые точки
которого содержат хотя бы одну
целочисленную координату.
выпуклой оболочке все угловые точки
имеют только целочисленные координаты,
но из-за трудности ее построения оболочки
строится «промежуточный» многогранник,
охватывающий всю целостную оболочку;
полностью содержащийся в области
допустимых решений, угловые точки
которого содержат хотя бы одну
целочисленную координату.
Такое построение осуществляется путем введения на каждом шаге дополнительного линейного ограничения, который уменьшает исходный многогранник решения путем отсечения от него некоторой части, при этом не исключая ни одного целочисленного решения.
Кроме того, ограничение строится так, чтобы его плоскость проходила хотя бы через одну точку, имеющую хотя бы одну целочисленную координату. За конечное число шагов данный метод приводит к новой задачи, оптимальное решение которой является и оптимальным решением и целочисленной задачи.
Для изложения вводим следующие понятия:
Пусть а - действительное число. Целой частью числа а – [a] – есть максимальное целое, не превосходящее данного числа. Дробная часть числа а – qa- разность между числом и его целой частью: qa= а-[a]; 0≤ qa≤1
Основным понятием в методе отсечения является понятие «правильного отсечения».
Определение: пусть Х*- оптимальный нецелочисленный план (ослабленной задачи). Неравенство х< называется правильным отсечением (отсечением Гомори), если оно удовлетворяет следующим условиям:
условие отсечения: Х* не удовлетворяет этому ограничению х*≥
условие правильности: для всякого произвольного целочисленного плана Х` Х`<
Необходимым условием применения первого алгоритма Гомори (аддитивного) является целочисленность всех коэффициентов и элементов правых частей.
Алгоритм Гомори состоит из двух шагов:
Решается ослабленная задача симплекс-методом. Если оптимальный план целочисленный, то он является решением исходной задачи, в противном случае переходим к пункту № 2.
Вводится дополнительное линейное ограничение - правильное отсечение и переходим к пункту № 1, решая ослабленную задачу с дополнительным ограничением.
Процесс присоединения дополнительных ограничений продолжается до тех пор, пока:
Либо не будет найдено целочисленное решение задачи
Либо не будет установлено, что такого решения нет.
Условие неразрешимости целочисленной задачи:
Это возможно, если для дробного значения переменной задачи xj (которая не является недобавочной, неизбыточной переменной) все коэффициенты aij в данной строке симплекс-таблицы оптимального решения окажутся не целыми.
Схема алгоритма
Пусть в результате решения ослабленной задачи получен оптимальный план, имеющий хотя бы одну нецелочисленную компоненту.
Замечание: 1-й алгоритм Гомори решает только полностью целочисленные задачи, поэтому результатом его решения может быть оптимальный план только с целочисленными компонентами.
В симплекс-таблице оптимального решения выбираем значение базисной переменной задачи Х*j с наибольшей дробной частью. Если таких переменных несколько, то выбираем любую.
Этой переменной соответствует строка симплекс-таблицы, называемая строкой, производящей отсечение (производящей строкой).
Выписывается уравнение
![]() (полагая,
что первые
m
переменных базисные для данного
оптимального решения).
(полагая,
что первые
m
переменных базисные для данного
оптимального решения).
На основании этой строки, предполагаем, что m первые переменные являются базисными, и т.к. коэффициенты целевой функции - целые числа, то значение целевой функции на целочисленном решении также должно быть целочисленно.
Представим каждый коэффициент данной строки в виде целой и дробной частей.
Тогда
![]() 0<qj<1
0<qj<1
![]() 0≤qj<1
0≤qj<1
qj - положительная дробь
qij - неотрицательная дробь
Переносим все целые части коэффициентов в одну сторону, оставляя все дробные в другой:
![]()
Так как все переменные xm+1,...,xn принимают целочисленные значения и силу их небазисности, то правая часть уравнения является целочисленной. Следовательно, в силу неотрицательности дробных частей и переменных задачи и левая часть должна быть неотрицательна:
![]() ,
следовательно,
,
следовательно,
![]()
Так
как qj<1,
заменяя в правой части qj,
получим строгое неравенство
![]()
Так
как левая часть неравенства должна
принимать целые значения, то,
следовательно, необходимое условие
ее целочисленности
можно
записать только в следующем виде:
![]()
Вводя
остаточную переменную Sj
(переменную Гомори), получим
![]()
Где
Sj
–
неотрицательная добавочная переменная,
которая по определению должна принимать
целочисленное значение, что для данной
системы ограничений при xj=0
имеет вид:
![]()
Следовательно, она принимает отрицательное значение, т.е. является недопустимой, и, таким образом, полученное ранее решение ослабленной задачи не удовлетворяет данному ограничению. В этой ситуации обычно используют двойственный симплекс-метод или М-метод.
Вывод: строится ограничение, которому не удовлетворяет оптимальный нецелочисленный план. Следовательно, надо решить задачу с исходной целевой функцией и расширенной системой ограничений.
