Симплексный метод.

Основная идея: Симплекс метод – это направленный перебор опорных решений задачи линейного программирования, при котором значения целевой функции на каждом следующем шаге больше (не меньше), чем на предыдущих.

По процедуре метода переход от одной угловой точки к другой осуществляется с помощью преобразований Жордана - Гаусса. Преобразования осуществляются над строками матрицы и состоят в следующем:

1)перемена строк местами

2)умножение строки на число, отличное от нуля

3)сложение двух строк покомпонентно (элементов, стоящих в одном столбце).

Для решения задач симплекс- методом следует выполнить действия:

0) Построить экономико - математическую модель задачи

1. Привести задачу к канонической форме.

2. Составить исходную симплекс таблицу

3. Проверить план на оптимальность.

4. Если план не оптимальный, то переходим к новому опорному плану с помощью преобразований Жордана-Гаусса.

Теорема 3. 1: «Признак оптимальности»

План X^* для задачи на максимум (минимум) - оптимальный, если в индексной строке симплекс-таблицы все оценки неотрицательные (не положительные).

Задача № 1.

Предприятие планирует выпуск трех видов изделий и при этом предполагает использовать три вида ресурсов. Известны цена реализации (прибыль) единицы каждого вида изделия C₁,C₂,C₃, запасы ресурсов каждого вида В_1, В_2, В_3, расходы каждого вида ресурсов на производство единицы каждого вида продукции a_ij. Требуется составить план производства ( указать сколько и какой продукции надо выпускать, чтобы получить максимальную прибыль от ее реализации).

1. Составление экономико-математической модели:

В качестве переменных Х_1,Х_2,Х₃ выбираем количество продукции каждого вида. Следовательно, значение этих переменных неотрицательно.

2. Целевая функция выражает прибыль от реализации и, следовательно, имеет представление Z=C₁X₁+C₂X₂+C₃X₃ и исходя из содержания задачи она должна быть максимальной.

3. Ограничения:

• Не отрицательность переменных из пункта а)

• Ограничение по ресурсам. Расход каждого вида ресурса на производство всех видов продукции не превосходит их заданных объемов:

a₁x₁+…..+a_1nx_n≤b₁

……………

a_m1x₁+…..+a_mnx_n≤b_m

Из содержания задачи b₁ и b_m должны быть положительны, т.к. это запасы ресурсов.

Д ано: C₁=5, C₂=4, C₃=3 , a_ij

В₁=50, В₂=60, В₃=30.

Целевая функция Z=5x₁+4x₂+3x₃ max выражает собой прибыль от реализации продуктов.

4x₁+3x₂+x₃ 40

2x₁+5x₂+2x₃ 50

x₁+2x₂+4x₃ 60

x₁,x₂,x₃ 0

Для решения задачи симплекс-методом приводим ее к канонической форме. В данном случае не выполняется лишь одно условие канонической формы, а именно ограничения должны быть типа равенства. Для перехода к ограничениям типа равенства в левую часть каждого из неравенств вводится своя неотрицательная добавочная переменная (в случае если левая часть меньше или равна правой), и избыточная неотрицательная переменная вычитается (в случае если левая часть больше или равна правой), которые входят в функцию цели с нулевыми коэффициентами.

Z =5x₁+4x₂+3x₃+0x₄+0x₅+0x₆ max

x₁+3x₂+2x₃+x₄ =40

4x₁+x₂+x₃+x₅ =50

2x₁+2x₂+x₃ +x₆=60

x₁,x₂,x₃,x₄,x₅,x₆ 0

Это есть каноническая форма задачи. Для решения симплекс-методом составляется исходная симплекс-таблица.

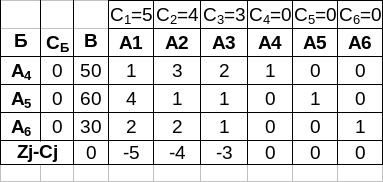
Т.к. симплекс-метод есть направленный перебор угловых точек (опорных решений), то необходимо определить исходное опорное решение, отправляясь от которого с помощью процедур симплекс-метода определим хотя бы одно оптимальное или установим неразрешимость задачи.

Каждое опорное решение определяется некоторым базисом векторов-условий, и т.к. размерность векторов равна 3, то базис должен содержать ровно 3 вектора. Из канонической формы задачи определяем «явные» базисные вектора размерностью три А₁, А₂, А₃, т.к. это три единичных вектора размерностью три, которые образуют базис. Следовательно, все остальные переменные Х_1,Х_2,Х₃ должны быть равны нулю. Из уравнения канонической формы видно, что Х₄=50, Х₅=60, Х₃=30.

Таким образом, получим исходный опорный план Х₀=(0,0,0,50,60,30), значение целевой функции на котором равно нулю, что соответствует естественной постановке задачи, а именно если ничего не производится Х_1,Х_2,Х₃=0, то и прибыль отсутствует. В столбец B заносим коэффициенты целевой функции при базисных переменных. В столбец В заносим значения базисных переменных.

m+1 строка называется строкой оценок или индексной (Z_j – C_j)

Z_j – значение функции цели на j-векторе и равно скалярному произведению двух векторов С_Б и А_j: Z_j=С_Б*A_j

На пересечениях индексной строки и столбца В находятся значения целевой функции на данном опорном плане.

Теорема 4.1. «Критерий оптимальности линейной задачи»

План оптимальный в задаче на максимум (минимум), если все оценки индексной строки не отрицательные (не положительные).

Следствие:

Если среди оценок индексной строки есть отрицательные, то данный план неоптимальный и его можно попытаться улучшить с помощью преобразований Жордана-Гаусса (согласно следующей теореме).

Теорема 4.2 «О переходе к новому опорному плану»

Для перехода к новому опорному плану (к новому базису отличного от данного) будем следовать следующим правилам: