Метод ветвей и границ.

Идея метода: пусть решена задача без условия целочисленности и х^*_r – целочисленная переменная, значение которой в оптимальном плане является дробным. Тогда интервал [х^*_r]< х _r<[х^*_r]+1 не содержит допустимых решений с целочисленной координатой х_r. Следовательно, допустимое решение с целочисленной координатой х_r удовлетворяет одному из следующих условий : [ х _r≤[х^*_r] или х _r≥[х^*_r]+1.

Введение этих условий в исходную задачу порождает две несвязанных между собой задачи с одной и той же целевой функцией, но не пересекающихся областями допустимых решений. В этом случае говорят, что задача разветвляется.

Осуществляемый в процессе учет необходимых условий целочисленности позволяет исключить часть многогранника решений, не содержащих решений с целочисленной координатой х _r.

Геометрическая интерпретация:

В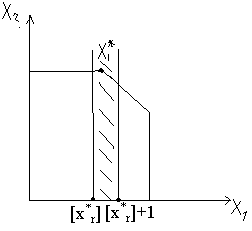 ырезаем «полосу», не содержащую решение с целочисленной координатой х₁. Затем решаем каждую из подзадач. Если полученный оптимум окажется допустимым для целочисленной задачи, то значение его фиксируется как наилучшее, и при этом нет необходимости продолжать ветвление данной подзадачи. В противном случае подзадача, в свою очередь, разбивается на две подзадачи при условие целочисленности значений, которые в оптимальном плане не оказались целыми. Как только полученное допустимое целочисленное решение одной из подзадач окажется лучше имеющегося, то одно фиксируется вместо зафиксированного ранее.

Процесс ветвления продолжается до тех пор, пока не приведет к целочисленному решению или пока не будет установлена невозможность сосуществования такого, либо улучшение уже имеющегося.

Эффективность вычислительной схемы существенно повышается с введением понятия «граница», на основе которого делается вывод о необходимости дальнейшего разбиения каждой из подзадач.

Суть: если оптимальное решение подзадачи без условия целочисленности обеспечивает худшее значение целевой функции, чем имеющееся ранее, то подзадача далее не рассматривается, и говорят, что она прозондированна, и ее можно вычеркнуть из списка подзадач, порожденных исходной задачей. Другими словами, как только получено допустимое целочисленное решение, соответствующее значение целевой функции может быть использовано в качестве верхней (в случае минимизации) или нижней (в случае максимизации) границы, наличие которой позволяет формализовать процедуру исключения прозондированных задач. Этот метод позволяет решать как полностью, так и частично целочисленные задачи.

Специальные виды целочисленных задач. Транспортная задача

1. Транспортная задача. Распределительный метод.

2. Метод потенциалов (Канторовича)

3. Задача о назначениях. Венгерский алгоритм.

Классическая транспортная задача – это задача о наиболее экономичном плане перевозок однородного (или взаимозаменяемых) продукта из заданных пунктов отправления (пункта производства или хранения) в пункты назначения (пункты потребления данного продукта). Наиболее часто встречается в распределительных экономических задачах.

Эта задача связана с территорией, распределением, назначениями, транспортом и размерами производства. Кроме того, различные варианты этой задачи встречаются в задачах организации производства, принятия решений и организационного управления.

Классическая подстановка: имеется m пунктов производства или складирования однородного продукта, запасы которого равны соответственно A₁…A_i….A_m. Имеется n пунктов потребления этого же продукта с потребностями В₁…В_j….В_n. Известны тарифы (транспортные расходы, связанные с доставкой единицы продукта из заданного пункта отправления в заданный пункт потребления)

Требуется составить план перевозок (указать какое количество из какого пункта отправления и в какой пункт потребления следует перевезти продукт), обеспечивающий наиболее экономичным путем (при суммарных минимальных затратах на перевозку) удовлетворение всех пунктов потребления за счет реализации всего продукта, находящегося в пунктах отправления.

Фактически требуется указать вектор поставок ( ), где x_ij – количество единиц продукта, направленного из i-го пункта отправления в j-й пункт потребления и удовлетворяющий следующим условиям:

1. Условие полного удовлетворения потребностей всех пунктов потребления.

2. Весь продукт, хранимый на базах, должен быть вывезен.

и дающий минимум целевой функции

Транспортная задача исследуется только на минимум.

Определение: Транспортная задача называется закрытой (сбалансированной), если суммарный объем запасов равен суммарному объему потребностей:

В противном случае она называется открытой.

Теорема 1 (необходимое условие разрешимости транспортной задачи)

Транспортная задача разрешима тогда и только тогда, когда она сбалансированная.

Если задача открытая, то ее всегда можно привести к закрытой, при этом следует произвести следующие преобразования:

а) Случай дефицита (суммарное потребление строго больше суммарных запасов). В этом случае вводят фиктивный пункт отправления с запасами, равными , из которого перевозка во все пункты назначения осуществляется по нулевым тарифам.

б) Случай избытка продукта. Вводится фиктивный пункт потребления с потребностями , перевозки в который со всех пунктов отправления осуществляются по нулевым тарифам.