Теория двойственности в линейном программировании.

Важную роль в линейном программировании играют двойственные (сопряженные) задачи, особенно по отношению к задачам, связанным с планированием производства и распределением ресурсов. Допустимое решение прямой и двойственной задач прямо связаны между собой, однако, их оптимальные решения таковы, что зная одно из них, сразу же определить оптимальное решение другой.

Часто решение двойственной задачи найти намного легче, чем решение прямой.

Прямая задача: предприятие имеет m-видов ресурсов в количестве b_i (i= ), из которых планируют произвести n – видов продукции : j= . Для производства единицы j-ого вида продукции предполагается использовать a_ij-единиц i-того вида ресурсов, цена реализации единицы продукции равна c_j. Требуется указать сколько и какого вида продукци следует выпускать, чтобы обеспечить максимальную прибыль от ее реализации.

Формально, следует определить вектор Х=(x₁,…,x_n) удовлетворяющими ограничениям

a₁₁x₁+…+a_1nx_n b₁

……………………

a_m1x₁+…+a_mnx_n b_m

x_j 0 j=

и обеспечивающей максимум функции Z=С₁Х₁+…+С_nХ_n

Оценим стоимость ресурсов, необходимых для производства продукции указанных видов.

За единицу оценки стоимости ресурсов принимают единицу стоимости выпускаемой продукции.

Через y_i обозначим оценку стоимости единицы i-того вида ресурса. Тогда оценка стоимости ресурсов, затраченных на изготовление единицы j-ого вида продукции, будет равна a_ijy_i– и она не меньше стоимости выпускаемой продукции a_ijy_{i сj} j= . При этом оценка стоимости затраченных ресурсов выражается b_iy_i min. Формально требуется определить вектор Y=(y₁…..y_m), удовлетворяющий ограничениям:

a₁₁y₁+…+a_1my_m c₁

……………………...

a_n1y₁+…+a_nmy_m c_n

y_{i 0} i=

и обеспечивающий минимум целевой функции F=b₁y₁+...+b_my_m min.

Стоимостное выражение ресурса не есть его цена и поэтому y₁…y_m – это есть неявные или учетные цены.

Экономическая интерпретация

Прямая: сколько и какой продукции необходимо произвести, чтобы при заданных ценах реализации, объемах и заданном способе производства получить максимальную прибыль от реализации произведенной продукции. Z=CX max AXB X0

Двойственная: какова должна быть оценка цены единицы каждого вида ресурсов, чтобы при имеющихся их объемах, величин стоимости реализации и заданном способе производства, минимизировать общую оценку стоимости затрат. F=BY min A^TYC Y0

Виды моделей двойственных задач.

1.Не симметричные
Прямая	Двойственная
1)Z=CX max AX=B X 0	1)F=YB min YA^T C
Симметричные
1)Z=CX max AX B X 0	1)F=BY min A^TY C Y 0

Соответствие между прямой и двойственной задачами.

Прямая	Двойственная
1)Целевая функция исследуется на max	1)Целевая функция исследуется на min
2) коэффициент целевой функции C=(C1…Cn) – вектор-строка	2)Вектор-столбец ограничений
3) матрица ограничений – А	3)Транспонированная матрица A^T
4)B=( ) вектор–столбец ограничений	4)Коэффициент целевой функции В=(b1……bn) – вектор-строка
5)Неравенство в ограничениях: правых частей	5)  правых частей
6)Ограничения: I-ограничение неравенства i-ограничение равенства	6)Ограничения: Yj 0 На переменную Yj нет ограничений на знак.
7)Переменные: а) Xj 0 переменные неотрицательны б) на переменную Xj – нет ограничений на знак	7) Переменные: а) J-е ограничение-неравенство б) J-е ограничение равенство

Число ограничений двойственной задачи равно числу переменных прямой, а число переменных двойственной задачи равно числу ограничений прямой.

Теорема 6.1 «Первая теорема двойственности»

Для любой пары двойственных задач имеет место одно из следующих вариантов:

1. Прямая и двойственная задачи имеют оптимальные решения тогда, когда значения целевой функции (на оптимальных решениях этих задач) совпадают.

2. Целевая функция прямой задачи не ограничена сверху на не пустом множестве планов, тогда двойственная задача имеет пустое множество допустимых решений.

3. Прямая и двойственная задачи могут иметь пустые множества допустимых решений.

4. Если множество допустимых решений одной из двойственных задач пусто, то целевая функция другой задачи не ограничена.

Лемма 1.

Для любых планов X и Y прямой и двойственной задач соответственно (прямая – максимум, двойственная – минимум) имеет место Z(X*) F(Y*), где Z – целевая функция переменной, F – функция двойственной задачи.

Теорема 6. 2 «Вторая теорема двойственности»

Пусть X^*=(X ,…X ) и Y^*=(Y ,…Y ) допустимые решения прямой и двойственной задач соответственно. Для того, чтобы X* и Y* были оптимальными решениями прямой и двойственной задач, необходимо и достаточно выполнение следующих условий:

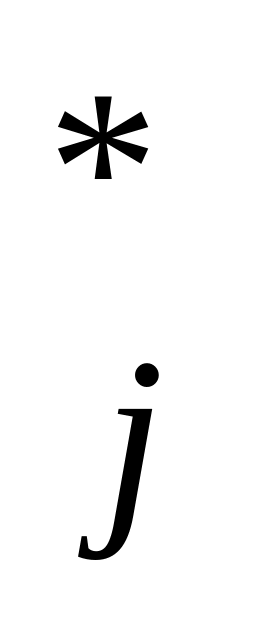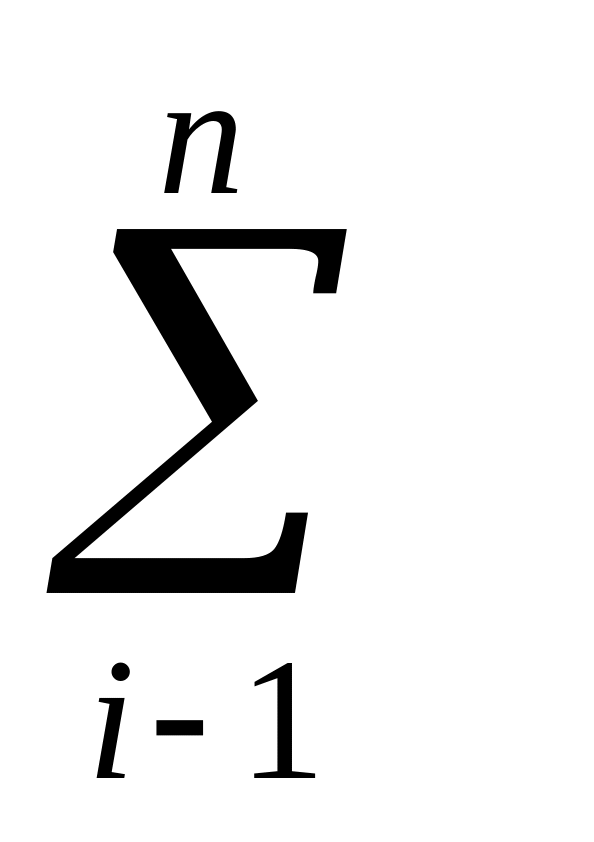1. x ( a_ijy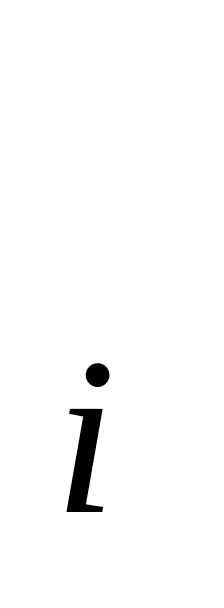^* -c_j)=0 j=

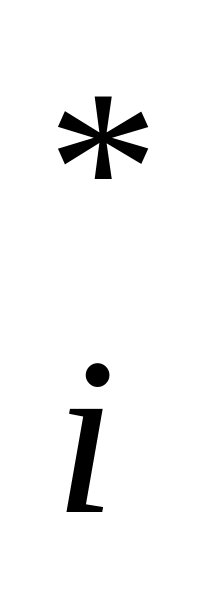2. y ( a_ijx^*_j-b_i)=0 i=

Условие 1 и 2 позволяют, зная оптимальное решение одной из задач, найти оптимальное решение другой. На основании второй теоремы двойственности сформулируем критерий оптимальности для допустимого решения задачи.

Теорема 6.3.

Пусть X^*=(X ,…X ) допустимое решение прямой задачи. Вектор X^* является оптимальным решением прямой задачи тогда и только тогда, когда среди решений системы уравнений (1) при X 0 содержалось хотя бы одно допустимое решение двойственной задачи, в которой y_i=0 при a_ijx_j<b_i.