1. Коефіціент кореляція

Кореляція є залежністю двох випадкових величин. При цьому, зміна однієї або кількох цих величин призводить до систематичної зміни іншої або інших величин. Математичною мірою кореляції двох випадкових величин слугує коефіцієнт кореляції.

Кореляція може бути позитивною та негативною (можлива також ситуація відсутності статистичного зв'язку - наприклад, для незалежних випадкових величин). Від'ємна кореляція – кореляція, при якій збільшення однієї змінної пов'язане зі зменшенням іншої, при цьому коефіцієнт кореляції від'ємний. Додатна кореляція – кореляція, при якій збільшення однієї змінної пов'язане зі збільшенням іншої, при цьому коефіцієнт кореляції додатній.

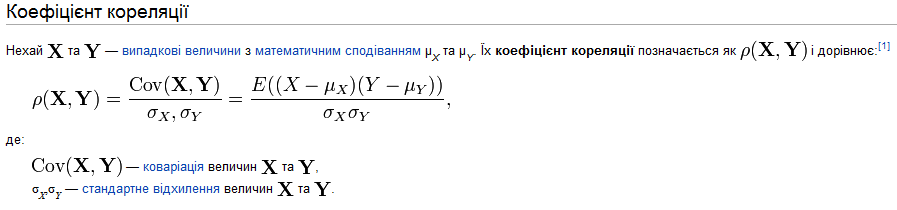
2 Числові характеристики випадкових величин.

Найбільш повна характеристика випадкової величини дається її функцією розподілу (або також і щільністю розподілу для неперервної випадкової величини). Проте досить часто доцільно обмежитися простішою, хоч і неповною інформацією про випадкову величину. Наприклад, досить вказати окремі числові величини, які певним чином визначають істотні риси розподілу випадкової величини: деяке середнє значення випадкової величини; деяке число, що характеризує ступінь розсіювання значень випадкової величини навколо її середнього значення, тощо. Користуючись такими характеристиками, ми в стислій формі можемо отримати інформацію про істотні особливості законів розподілу випадкової величини.

Характеристики, що виражають в стислій формі найістотніші особливості закону розподілу випадкової величини, називаються числовими характеристиками випадкової величини.

До них в першу чергу відносяться математичне сподівання і дисперсія.

5.1. Математичне сподівання.

Випадкова величина може приймати різні числові значення, тому практично важливим є середнє значення випадкової величини. Для оцінки середнього (у ймовірнісному сенсі) значення випадкової величини вводиться поняття математичного сподівання, яке є дійсним середнім значенням випадкової величини і визначається з врахуванням різних ймовірностей її окремих значень.

Математичне сподівання випадкової величини позначаємо . Для дискретної випадкової величини , заданої рядом розподілу

			…		…		…
			…		…		…

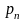
де , математичне сподівання обчислюється за формулою

= , (1)

якщо ряд справа збігається.

Нехай - неперервна випадкова величина, значення якої , і - її щільність розподілу. Розіб’ємо відрізок на частин, довжини яких , ,…, . Візьмемо в кожному частинному відрізку точку . Добуток приблизно дорівнює ймовірності попадання неперервної випадкової величини в інтервал , а сума наближено дорівнює математичному сподіванню неперервної випадкової величини. Якщо існує границя , то вона називається математичним сподіванням неперервної випадкової величини і позначається = . (2)

У випадку, якщ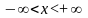о , то = , причому інтеграл повинен збігатися абсолютно. Відзначимо найпростіші властивості математичного сподівання:

. ; де - стала величина,

. ;

. + ;

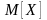. ; якщо випадкові величини незалежні.

Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша випадкова величина.

Математичне сподівання називають центром розподілу ймовірностей випадкової величини , випадкова величина називається центрованою.

5.2. Дисперсія.

Для характеристики розсіювання значень випадкової величини відносно її центра розподілу (математичного сподівання) вводять числову характеристику – дисперсію випадкової величини. Позначається . За означенням, дисперсією випадкової величини називається математичне сподівання квадрату відхилення випадкової величини від її математичного сподівання

= . (3)

Дисперсія обчислюється за формулами

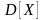= (4)

для дискретних випадкових величин, і

= (5)

для неперервних випадкових величин. Тут для простоти позначено = .

Найпростіші властивості:

. ; де - стала величина,

. ;

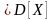. + ; якщо випадкові величини незалежні.

Практично дисперсію обчислюють за робочою формулою

= , (6)

де для дискретних випадкових величин і

для неперервних випадкових величин.

Дисперсія є кількісною оцінкою відхилення випадкової величини від її математичного сподівання. Проте, оскільки дисперсія має розмірність квадрата випадкової величини, то для оцінки міри розсіювання використовують характеристику , яка називається середнім квадратичним або стандартним відхиленням випадкової величини. Оскільки , то і

. Розмірність середнього квадратичного відхилення співпадає з розмірністю випадкової величини.

3. Перш ніж аналізувати основну тенденцію (тренд) або циклічніколивання, необхідно виключити сезонну компоненту і перевірити гіпотезу проіснування тренду.

Для цього можна використовувати метод перевірки різниць середніх рівнів. Суть цього методу полягає в поділі ряду на дві частини і знаходженні їх середніх і дисперсій за формулами. Потім ми знаходимо розрахункове значення за допомогою статистики Стьюдента

Потім отримане значення порівнюємо з критичним табличним значенням.

Порівнявши критичне значення з розрахунковим, робимо висновок про наявність чивідсутності тренда в риду динаміки.