Інтеграли

Розділ 6. ІНТЕГРАЛ ТА ЙОГО ВИКОРИСТАННЯ

План

1. Первісна та невизначений інтеграл.

2. Основні властивості невизначеного інтеграла.

3. Таблиця невизначених інтегралів.

4. Визначений інтеграл.

5. Формула Ньютона – Лейбніца.

6. Використання визначених інтегралів для обчислення площ плоских фігур.

7. Приклади для розв’язування задач.

1. Первісна та невизначений інтеграл.

В багатьох практичних задачах необхідно по заданій похідній відновити первісну функцію.

Означення. Функція F(x) називається первісною для функції f(x) на проміжку (а; b), , якщо на цьому проміжку .

Операція знаходження первісних для функції f(x) називається інтегруванням f(x).

Означення: Невизначеним інтегралом для неперервної функції називають множину всіх первісних функцій і позначають

де:

— знак невизначеного інтеграла;

f(x) — підінтегральна функція;

f(x) dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

2. Основні властивості невизначеного інтеграла.

1) ;

2) ;

3) ;

4) .

3. Таблиця невизначених інтегралів.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17.

1. Визначений інтеграл

В изначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний смисл цього визначеного інтеграла — це площа криволінійної фігури, обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.

6.Формула Ньютона – лейбніца.

Якщо у функції f(x) існує первісна F(x), то

7. Використання інтегралів для обчислення площі плоских фігур

№ п/п	Назва поняття.	Геометричне зображення	Формула для обчислення.
1.	П лоща криволінійної трапеції, якщо 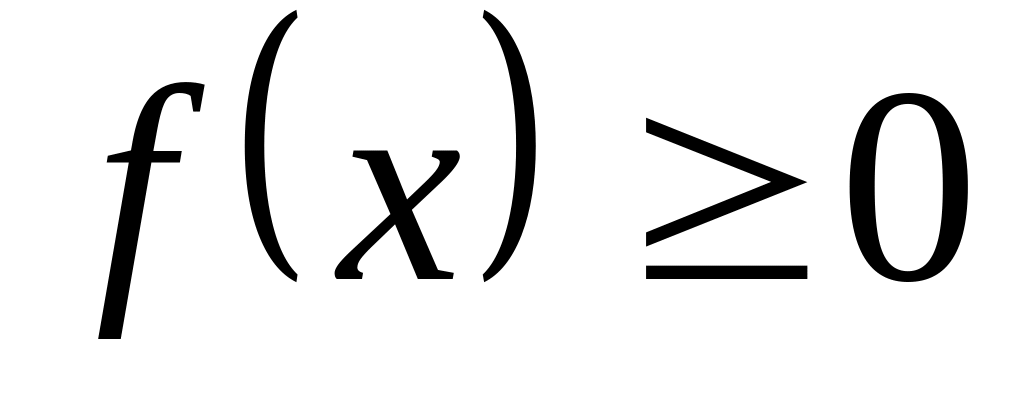на відрізку
2.	Площа криволінійної трапеції, якщо на відрізку
3.	Якщо фігура обмежена графіками неперервних на відрізку функціями і , при чому
4.	Я кщо функціями кілька разів змінює знак на відрізку , то інтеграл для обчислення площі на всьому відрізку розбиваємо на частини. Інтеграл буде додатній на тих частинах, де і від’ємний там де .

1. Приклади для розв’язування.

1. Знайти невизначені інтеграли.

2.** Знайти невизначені інтеграли.
3.* Знайти невизначений інтеграл методом заміни змінної.
4. **Знайти невизначений інтеграл методом заміни змінної.
5. ***Обчислення невизначеного інтеграла методом заміни змінної
	21.
6. Обчислити визначений інтеграл.

7. **Обчислити площі плоских фігур, обмежених лініями:

1. х – у + 2 = 0 2. 2х – 3у + 6 = 0; 3. х – у + 3 = 0; 4. х – 2у + 4 = 0 5. у = х^2 6. у = 3 х^2 ; 7. у = х^2 + 1; 8. у = 0,5х^2 + 2; 9. у = - (1/3)х^2 + 3; 10. у^2 = х; 11. у = - х^2 – 2х + 8; 12. у = - (2/9)х^2 + (4/3)х; 13. у = - х^2 + 6х -5; 14. у = 1/х; 15. у = 2/х; 16. у = соs x, 17. y = tg x, 18. y = tg x, . 19. y = - 3x, 20. y = 2x, 21. x – 2y – 6 = 0, 22. x – 2y – 5 = 0, 23. y = - 3x^2 , 24. y = - x^2 – 1, 25. y = x^2 – 4, 26. y = x^3 , 27. y = 4 x^3 , 28. y^2 = 4x, 29. y^2 = 9x, 30. y = sin x, 31. y = sin x, 31. y = x^2 , . 32. y = x^2 , 33. y = x^2 , 34. y = x^2 + 2 , 35. y = 0,5x^2 – 4x + 10, 36. y = x^2 – 2x + 3, 37. y =(1/3)x^2 – 2x + 4, 38. y = 0,5x^2 + 2x + 4, 39. y = 2x^2 + 1, 40. y = - 1,5x^2 + 9x – 7,5, 41. y = x^2 , 41. y = x^2 – 6x + 9, 42. y = x^2 , .

у = 0; у = 0; х + у – 1 = 0; х + 2у – 8 = 0, у = 0 у = 0; у = 0 у = 0 у = 0 у ≥ 0; у = 0. у = 0. у = 0; у = 0; у = 0; y = 0 y = 0, y = 0, y = 0, y = 0, y = 0. y = - 2x, y = 0, y = 0, . y = 0. y = 0 y = 0, x = 1, x = 4, y = 0, y = 0, y = - 3x y = 2x + 8. y = x + 2. y = 6. y = x + 2. y =3 x – 1 y = - x + 10. y = x + 8. y = x^2 + 10. y = - x^2 +6x - 5. y = 2 – x^2 . 3x – y – 9 = 0. x = y^2 .

х = - 1; х = 3, у = 0; у = 0 х = 0, х = - 3; х = - 1; х = 1 х = 0; х = 0; х = 3. х = 1; х = 2; x = 0, x = 0, x = π/6, x = 2. x = - 3. y = 0 x = 1, x = - 2 x = - 2, x = - 1, x = 9. x = - π/2 x = 0,

х = 2, х = - 1; х = 6 х = 3. х = 2 х = 2. х = 3. х = 3. х = 3 х = 2; х = 3 х = 4 x = π/2. x = π/3 x = π/3 x = 2. x = 1 x = 2 x = 2. x = π. x = 2π.

10