Необходимое условие существования экстремума.

Теорема Ферма. Если внутренняя точка х₀ из области определения непрерывной функции f(х) является точкой экстремума и в этой точке существует производная, то она равна нулю, т. e.f '(x₀) = 0.

Чтобы определить, имеет ли функция экстремум в данной точке, необходимо воспользоваться достаточными условиями его существования.

Достаточные условия существования экстремума

Теорема 1. Если существуют такие а и b, что функция f(х), непре­рывная в точке х₀

(а < х₀ < b), такова, что f(x) > 0 на интервале (а, x₀) и f '(х) < 0 на интервале (х₀, b), то точка x₀ является точкой максимума функции f(х).

Теорема 2. Если функция f (х) непрерывна в точке х₀, a f '(x) < 0 на интервале (а, х₀) и f ′(x) > 0 на интервале (х₀, b), то точка х₀ является точкой минимума функции f(x).

Таким образом, чтобы найти экстремумы данной функции у = f(х), необходимо:

1. Найти первую производную f '(х).

2. Приравняв первую производную нулю, отыскать действительные корни х₁, х₂,. . . уравнения f '(х) = 0.

Корни этого уравнения являются критическими точками функции.

3. Для каждой критической точки х_k найти окрестность, не содержа­щую других критических точек, подставить в производную любое число, меньшее х_k из этой окрестности, а затем любое число, большее х_k, из этой окрестности; если при этом знак производной:

а) будет меняться с + на –, то функция при х = х₁ имеет максимум;

б) будет меняться с – на +, то функция при х = х₁ имеет минимум;

в) не меняется, то функция при х = х₁ экстремума не имеет;

4. Найти экстремальные значения функции.

Пример 1. Исследовать функцию 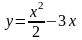, заданную на отрезке [0, 5], на экстремум.

Решение. 1) Находим производную: у' = х – 3.

2) Находим корень производной: х - 3 = 0 <=> х = 3.

3) Находим значение производной в точке х = 2 интервала (0, 3): y'(2) = -1 < 0.

4) Находим значение производной в точке х = 4 интервала (3, 5): y' (4) = 1 > 0.

Производная у' в окрестности точки х = 3 меняет знак с – на +, сле­довательно, в точке

х = 3 находится минимум.

5) находим значение функции в критической точке х = 3: у (3) = 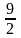- 3∙3 = - 4,5

Таким образом, минимальное значение функции равно -4,5.

Наибольшее и наименьшее значения функции

На рис. 3 изображен график некоторой функции у = f(х), определенной на отрезке

[а, b].

На данном отрезке наша функ­ция в точках х_1, х₂, х₃, х₄, х₅ прини­мает экстремальные значения. Для определения наименьшего и наи­большего значений дифференцируе­мой функции на всем данном отрезке [а, b] следует найти все критические точки функции, лежащие внутри отрезка, вычислить значения функции в этих точках и на концах отрезка и из всех полученных таким образом чисел выбрать наименьшее и наибольшее, т. е., как говорят, найти глобальные экстремумы функции.

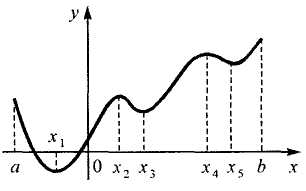
Рис. 3.

Пример 1. Найти наименьшее и наибольшее значение функции 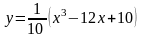на отрезке [-3, 4].

Решение. 1) Находим производную: .

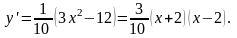2) Находим корни производной: х₁ = -2 и х₂ = 2.

3) Исследуем значение производной в окрестности критической точки х = -2:

y’(-3) = 1,5 > 0 и y’(-1) = -0,9 < 0. Следовательно, в точке x₁ = -2 данная функция имеет максимум, равный 2,6.

Аналогично находим, что в критической точке х₂ = 2 данная функ­ция имеет минимум, равный – 0,6.

В примере требуется найти наибольшее и наименьшее значение функ­ции в промежутке

[-3, 4], поэтому необходимо найти значение функции и на концах этого промежутка.

Имеем: у(-3) = 1,9 и у(4) = 2,6. Следователь­но, наименьшее значение, равное - 0,6, данная функция достигает в точке х = 2, а наибольшее значение 2,6 в двух точках: х = - 2 и х = 4.

Пример 2. Каковы должны быть размеры прямоугольной комнаты площадью 25м², чтобы периметр ее был наименьшим?

Решение. Примем длину комнаты равной х (м), тогда ширина равна 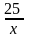, а периметр

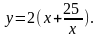
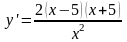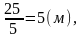Периметр у есть функция длины х, определенная для всех положи­тельных значений х. Определим интервалы ее возрастания и убывания. Находим производную: . Так как знаменатель больше нуля и длина х положительна, то знак производной определяется знаком разности (х - 5). Таким образом, периметр прямоугольника имеет наи­меньшее значение (минимум), если длина прямоугольника 5м и ширина т. е. когда комната имеет квадратную форму.