
- •Раздел 5. Дифференциальное исчисление.
- •5.2. Исследование функции с помощью производной Признаки возрастания и убывания функции
- •Необходимое условие существования экстремума.
- •Достаточные условия существования экстремума
- •Наибольшее и наименьшее значения функции
- •Выпуклость, вогнутость кривой. Точки перегиба.
- •Нахождение точки перегиба
- •План полного исследования функции и построение графика Общая схема исследования функции и построения ее графика.
Выпуклость, вогнутость кривой. Точки перегиба.
Исследование функции на экстремум и определение его типа (максимум или минимум) во многих случаях проще выполняется не путем анализа перемены знака производной при ее прохождении через критическую точку, а с помощью второй производной.
Определение 1. Непрерывная линия называется выпуклой или обращенной выпуклостью вверх на отрезке [а, b], если все точки этой линии лежат выше (не ниже) хорды, соединяющей любые две ее точки (рис. 4. а).
Аналогично, вогнутой (обращенной выпуклостью вниз) называется линия, проходящая ниже (не выше) своих хорд (рис. 4, б).
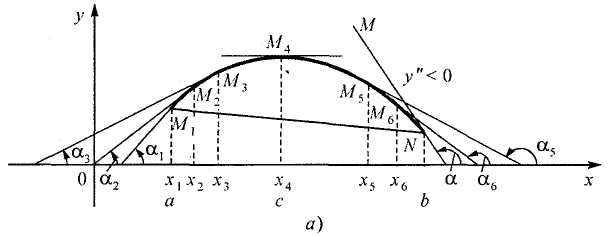
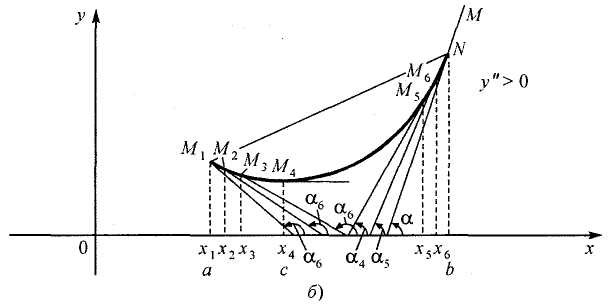
Рис. 4.
Замечание. В некоторых руководствах выпуклость и вогнутость иногда определяются противоположным образом.
Определение 2. Точки, отделяющие выпуклые участки линии от вогнутых (и наоборот), называются точками перегиба.
Теорема. Если вторая производная функции у = f(х) в данном промежутке значений х положительна, то кривая вогнута в этом промежутке, а если отрицательна — выпукла.
Точками перегиба являются те точки, при переходе через которые вторая производная меняет знак.
Линия называется выпуклой (или вогнутой) в точке, если значение ее второй производной в данной точке меньше (или больше) нуля.
Пример 1. Выяснить, выпуклая или вогнутая линия у = 3x3 + 8 в точке с абсциссой х = 3.
Решение. Находим производные у' = 6х2 и у" = 12х. В точке х = 3 имеем:
у"(3) = 12 • 6 = 36 > 0. Значит, в точке х = 3 данная линия вогнута.
Нахождение точки перегиба
Чтобы исследовать функцию на вогнутость, необходимо определить знак второй производной. Если на данном промежутке f "(х) < 0 для всех х, то линия вогнута, если f "(х) > 0 для всех х, то линия выпукла. Выпуклую часть кривой от вогнутой отделяет точка перегиба.
Правило нахождения точек перегиба
Чтобы найти точку перегиба линии у = f(х), нужно:
1. Найти вторую производную функции у = f(х).
2. Приравняв ее к нулю, решить полученное уравнение.
3. Расположив корни второй производной х1, х2, х3, ... в порядке их возрастания, подставить в выражение для второй производной сначала любое число, меньшее х1 затем — любое число
х
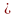 (х1, х2); если в обоих
случаях получатся разные знаки, то
при х = х1 имеется точка перегиба;
если же одинаковые, то точки перегиба
нет; аналогично определяется знак второй
производной и далее аналогично поступить
с числами х2, х3 и т.
д.
(х1, х2); если в обоих
случаях получатся разные знаки, то
при х = х1 имеется точка перегиба;
если же одинаковые, то точки перегиба
нет; аналогично определяется знак второй
производной и далее аналогично поступить
с числами х2, х3 и т.
д.
4. Найти ординаты точек перегиба, т. е. найти значения функции в соответствующих точках.
Пример 1. Найти точки перегиба линии f(х) = х3.
Решение. Находим: f '(х) = Зх2; f "(х) = 6х; 6х = 0 => х = 0; f(0) = 0.
Следовательно, A (0;0) – точка перегиба.
Пример 2. Найти точки перегиба линии у = х 4 - 2х2 - 3.
Решение. 1) у' = 4х3 - 4х; у" = 12х2 - 4.
2)
у" = 0 => 12х2 = 4; х
= ±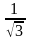 .
.
3) При |х| > имеем у" > 0 — линия вогнута; при |х| < имеем у" < 0 — линия выпукла. Точки ± являются точками перегиба (рис. 7).
Асимптоты графика функции.
Определение 1. Асимптотой графика функции y = f (x) называется прямая, обладающая тем свойством, что расстояние от точки M(x, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Определение 2. Прямая x = xo называется вертикальной асимптотой графика функции
y
= f(x),
если хотя бы один из односторонних
пределов f(xо–
0) =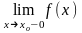 (предел слева) или f(xо
+ 0) =
(предел слева) или f(xо
+ 0) = (предел
справа) равен +
или -
(см. рис. 8).
(предел
справа) равен +
или -
(см. рис. 8).
Определение
3. Прямая
у = kx + b
называется наклонной асимптотой
графика функции y
= f(x)
при x +
+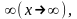 если
функцию y = f(x)
можно представить в виде
если
функцию y = f(x)
можно представить в виде
f(x) = kx + b + a(x),
где
a(x)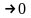 при x
при x
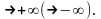
При x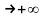 наклонная асимптота называется правой,
а при x
наклонная асимптота называется правой,
а при x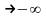 - левой. При k
= 0
- левой. При k
= 0
асимптота называется горизонтальной.
Теорема.
Для того чтобы график функции у =
f(x)
имел при
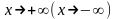 наклонную асимптоту y
= kx + b,
необходимо и достаточно, чтобы существовали
пределы
наклонную асимптоту y
= kx + b,
необходимо и достаточно, чтобы существовали
пределы
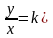 и
и
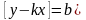 .
.
Пример
2. Рассмотрим функцию y
=
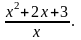
Так
как y = f(x)
= x + 2 +
 ,
где a (x)
=
,
где a (x)
=
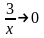 при x
при x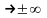 ,
то прямая у = x +
2 является левой и правой наклонной
асимптотой графика функции.
,
то прямая у = x +
2 является левой и правой наклонной
асимптотой графика функции.
Замечание. Для рациональной функции (отношение двух многочленов) левая и правая асимптоты совпадают.
