Н.С. ШУЛАЕВ, Т.В. ГРИГОРЬЕВА, Г.М.МИФТАХОВА

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ

НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Стерлитамакский филиал

Н.С. Шулаев, Т.В. Григорьева, Г.М. Мифтахова

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЗАДАЧ ФИЗИКИ И ГЕОМЕТРИИ

Учебное пособие

Уфа 2010

2УДК

ББК

Ш95

Утверждено Редакционно-издательским советом УГНТУ

в качестве учебного пособия

Рецензенты:

Зав. кафедрой автоматизации технологических информационных систем филиала УГНТУ в г. Стерлитамаке, доктор тех. наук, профессор А.И. Каяшев.

Кандидат физико – математических наук, доцент кафедры общей физики СГПА им. Зайнаб Биишевой Ягафарова З.А.

Шулаев Н.С., Григорьева Т.В., Мифтахова Г.М.

Ш95 Определённый интеграл и его приложения к решению задач физики и геометрии: учеб. пособие. – Уфа: Изд-во УГНТУ, 2010. – 136 с.

ISBN

Учебное пособие содержит методический материал по теории определённого интеграла, формированию и развитию профессионально-прикладного математического мышления у студентов в процессе решения задач физического и геометрического характера с использованием методов интегрирования.

Пособие содержит основные положения курса «Математики» для подготовки дипломированного специалиста по направлению 655400 – «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии» и составлено на основе учебного плана специальности 17.05.00. Наибольшее внимание было уделено вопросам, чаще других встречающимся в практических применениях. Теоретические сведения сопровождаются подробно разобранными примерами.

Книга предназначена преподавателям для проведения занятий со студентами изучающими интегральное исчисление по дисциплине «математика», а также для использования студентами всех форм обучения в процессе их самостоятельной работы над излагаемом учебном материалом.

УДК

ББК

ISBN

© Уфимский государственный нефтяной

технический университет, 2010

© Шулаев Н.С., Григорьева Т.В., Мифтахова Г.М., 2010

СОДЕРЖАНИЕ

1. Определённый интеграл	1
1.1.Площадь криволинейной трапеции	6
1.2. Понятие определенного интеграла	6
1.3. Теорема существования определенного интеграла (без доказательства)	8
1.4. Основные свойства определенного интеграла	9
2. Произвольная от определённого интеграла по переменному верхнему пределу	13
3. Формула Ньютона-Лейбница	16
4. Интегрирование по частям в определенном интеграле	20
5. Несобственные интегралы	23
5.1 Несобственные интегралы с бесконечными пределами интегрирования	24
5.2. Несобственные интегралы от разрывных функций	29
5.3.Интегралы, зависящие от параметра	31
6. Геометрические приложения определенных интегралов	45
6.1. Вычисление площадей плоских фигур	45
6.2. Длина дуги	55
6.3.Вычисление объёмов тел вращения	63
6.4. Вычисление объемов тел по известным поперечным сечениям	67
6.5.Площадь поверхности вращения	70
7. Приложения определенных интегралов к решению задач физики	73
7.1.Путь пройденный телом	73
7.2.Работа силы	76
7.3. Количество электричества	88
7.4. Вычисление давления	92
7.5. Кинематическая энергия	98
7.6. Статический момент	100
7.7.Координаты центра тяжести	101
8.Тестовые задания для самостоятельной работы	106
9.Физические задачи для самостоятельной работы	118
10. Приближенные методы вычисления определенных интегралов	119
СПИСОК ЛИТЕРАТУРЫ	135

1 Определённый интеграл

Мощным средством исследования в математике, физике, механике и др. дисциплинах, являются определенные интегралы – одно из основных понятий математического анализа.

Как известно, средствами элементарной геометрии можно вычислять площади и объемы лишь в очень не многих случаях, - например площади только таких плоских фигур, которые ограниченны прямолинейными отрезками и дугами окружностей.

Однако в связи с потребностями практики перед математикой возникла необходимость решения задач на вычисление площадей и объёмов произвольных фигур.

Вычисление площадей, ограниченных кривыми, вычисление длин дуг, объемов, работы, скорости, пути, моментов инерции, центра тяжести и т.д. сводятся к вычислению определенного интеграла.

1. Задачи, приводящие к понятию определённого интеграла.

а) Задача о площади криволинейной трапеции (приводящая к понятию определённого интеграла)

Пусть имеем плоскую фигуру, ограниченную дугой АВ, кривой y=f(x), где f(x)- Непрерывная, неотрицательная на отрезке [a;b] функция, осью Ох и прямыми x=a и x=b .

Такая фигура называется – криволинейной трапецией.

Требуется вычислить площадь данной криволинейной трапеции.

В элементарной геометрии дается определение понятию площади только такой фигуры, которая ограничена прямолинейными отрезками, дугами окружностей.

Поэтому перед нами стоит двойная задача:

1. Дать (согласно с нашими наглядными представлениями о площади) определение понятию площади криволинейной трапеции;

2. Найти способ конкретного вычисления этой площади.

Обе эти задачи будем решать одновременно. Отрезок [a;b] оси Ox называется основанием криволинейной трапеции.

Разделим произвольным образом основание криволинейной трапеции на какое-либо число n частей точками деления.

причем

Отрезки [ ],[ ],[ ],…,[ ] назовем частными отрезками.

Из точек деления отрезка [a,b] восстановим перпендикуляры к ось Ох до пересечения их с дугой АВ (см. рис.)

Тогда криволинейная трапеция разобьётся на n «полосок».

На каждом из частных отрезков [ ],[ ],[ ],…,[ ] возьмём произвольную точку; обозначим их, соответственно,

Из этих точек восстановим перпендикуляры к оси абсцисс до встречи с дугой АВ.

Заменим каждую из полосок прямоугольником с основанием, равным основанию полоски, и высотой, равной, соответственно, значениям функции f(x), вычисленным в точках .

В результате получим ступенчатую фигуру, ограниченную сверху ломанной линией. Очевидно, что площадь ступенчатой фигуры равна сумме площадей этих прямоугольников:

(1.1)

Все слагаемые этой суммы имеют один и тот же вид; они отличаются друг от друга только значениями индекса (указателя) при независимой переменной.

Для сокращения записи вводят символ (где греческая буква (сигма)представляет собой знак суммы)

(1.2)

Это обозначение читается как: Сумма всех слагаемых вида от i=1 до i=n .Давая I значения 1,2,3,…,n, мы получим последовательно все слагаемые суммы, а соединив их между собой знаком плюс, получим сумму в развернутом виде.

Т.к. отрезок [a;b] можно разбить на частичные отрезки, различными способами и в пределах каждого частичного отрезка можно вы выбрать точки также произвольным образом, то таких ступенчатых фигур можно построить на одном сегменте сколько угодно. При этом, очевидно, что вообще говоря, зависит как от способа разбиения отрезка [a;b] на части, так и от выбора точек .

Будем теперь неограниченно увеличивать число n делений отрезка [a;b]. Однако так, чтобы длина каждого частичного отрезка (обозначим её через ) стремилась к нулю.

Для каждого из таких разбиений будем выбирать точки и вычислять площадь ступенчатой фигуры.

При таком процессе площадь ступенчатой фигуры будет стремиться к определённому пределу, который и принимают за площадь криволинейной трапеции.

б) Задача о работе переменной силы (приводящая к понятию определённого интеграла)

Пусть некоторое тело движется по прямой Ох под действием силы F, направление которой совпадает с направлением движения, а величина зависит от места нахождения тела на прямой.

Принято говорить, что при таком перемещении тела сила F совершает некоторую работу.

Вычислим работу, совершаемую переменной силой при перемещении тела из одной точки а прямой Ох в другую точку b той же прямой.

Сначала, однако, надо выяснить, что вообще понимать под работой такой силы.

В школьном курсе физики дается определение только для работы постоянной силы: A=FS, где S-пройденный путь. В данной задаче действует переменная сила на пути от a до b она, вообще говоря, меняет свое значение от точки к точке.

Сила F есть некоторая функция абсциссы точки, в которой находится тело в рассматриваемый момент. F=F(x).

Пусть функция F(x) – непрерывная функция.

Перед нами стоит задача:

1) дать определение работы переменной силы(направление которой совпадает с направлением движения).

2)указать способ вычисления этой работы.

Разобьём отрезок [a;b] произвольным образом на n частей точками деления: . На каждом из частичных отрезков возьмём произвольно, по точке: .

Сила, действующая на тело в каждой из этих точек, соответственно

равна:

Допустим, что на каждой части сила F(x) сохраняет постоянное значение равное 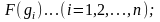(в силу того что частные отрезки весьма малы) тогда работа на первом частном отрезке равна На втором: и т.д.; на последнем На всём пути: или

(1.3) Будем неограниченно увеличивать число n делений [a;b] и притом так, чтоб длина каждого частного отрезка стремилась к нулю.

Если при неограниченном возрастании числа n, причем таком, что (I=1,2,…,n) сумма (1) стремится к определенному пределу А, не зависящему от выбранной системы разбиений и от выбора точек , то этот предел называется работой переменной силы F=F(x), на отрезке [a;b]:

(1.4)

Определённый интеграл широко применяется в естественных и в технических расчетах. При рассмотрении различных вопросов геометрии, физики, химии, биологии часто приходится составлять интегральную сумму и вычислять её пределы.

Рассмотрим, как с помощью определённого интеграла находить площади плоских фигур, объемов тел, длины дуг простых кривых, и т.д.

Схема применения определённого интеграла к нахождению геометрических и физических величин.

Рассмотрим схему, которой следуют, желая применить определенный интеграл к различным практическим задачам.

Эта схема вытекает непосредственно из задач(о вычислении площади криволинейных трапеции и работы переменной силы), приводящих к понятию определенного интеграла.

По этой схеме, для определения какой-нибудь неизвестной величины Q, которую невозможно измерить или вычислить непосредственно, поступают следующим образом:

Во всех задачах искомая величина связана с некоторой функцией, заданной на отрезке [a;b].

Отрезок [a,b] разбивают на частичные отрезки .

Каждой из этих частей соответствует своё значение величины Q:

Где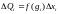 (1.5)

-длина частичного отрезка

(1.6)

-любое промежуточное значение

Выражение интегральная аргумента x на частичном отрезке.

Сумма для функции f(x) предполагая, что длины всех частичных отрезков неограниченно убывают, находим так . (1.7)