4. Определенный интеграл

4.1. Определение интеграла по Риману

 

         Пусть f(x) - функция, непрерывная на данном отрезке [a,b], где a < b  (a>b), и

F(x) - некоторая первообразная при х[a,b].

         Разобьем отрезок [a,b] на n частей

                                                    а = х₀ < x₁ < x₂ < ... < x_n = b.                          (4.1)

Обозначим длину отрезка х_i-1, х_i (i = 1k) через  х_i = х_i - х_i-1.

Тогда величина                                                                               (4.2)

 

называется мелкостью разбиения.

         Зафиксируем произвольным образом точки

_ix_i-1,x_i,    i=1,2,...,k

и составим сумму

                            .                                                     (4.3)

         Суммы вида (4.3) называются  интегральными суммами Римана.

 

Определение 4.1. Функция f называется интегрируемой (по Риману) на отрезке a,b, если существует такое число А, что  любой последовательности разбиений отрезка a,b, у которой    и для любого выбора точки _i х_i-1,х_i, (i=1n) выполняется равенство

                                                       ,                                      (4.4)

где

  (i=1k, n=1,2, ...).

 

Если выполнены все условия определения 4.1, то число А назовем (Римановым) определенным интегралом функции f на отрезке a,b и будем обозначать

                                                      .                                                      (4.5)

         Таким образом,

,где  ,или подробно

                                   .                               (4.6)

 

Определение 4.2. Число А называется определенным интегралом функции f на отрезке [a,b], если для  0  =()0 : для любого разбиения   [a,b], мелкость которого меньше _i _, каковы бы ни были точки _ix_i-1,x_i, то будет выполнено неравенство

,

 где х_i=х_i-х_i-1, i=1k.

 

         Если F(x) - первообразная, то под определенным интегралом понимается соответствующее приращение первообразной на a,b, то есть

                                                                                       (4.7)

(формула Ньютона-Лейбница).

4.2. Свойства определенного интеграла

         1.  .

         2. Если f интегрируемая на a,b тогда она интегрируемая на любом a^*,b^*  a,b. Кроме того, будем считать, что для всех f(х), имеющий смысл в точке a, тогда

.

         3. Пусть a<c<b. Если f(x) интегрируемая на a,c и c,b тогда она интегрируемая и на a,b, причем

                            - (aддитивность).                            (4.8)

         4. Если функции f и g интегрируемые на a,b, а  - некоторые константы, то их сумма f + g так же интегрируемая на a,b

                    - (линейность).      (4.9)

         5. Определенный интеграл от непрерывной функции не зависит от выбора первообразной для подынтегральной функции.

         6. Если f интегрируемая на a,b, a C - const следовательно cf также интегрируемая на a,b и

.

         7. Если f(x), g(x) - интегрируемые на a,b, их произведение f(x)g(x) также интегрируемое на   a,b.

         8. Если f(x) и g(x) интегрируемые на a,b и f(x)g(x)  х a,b 

                   а)  .

                   б)  .

                   в)  ,  (a < b).

         9. Если f(x)  интегрируемая на a,b тогда и f(x) также интегрируемая на 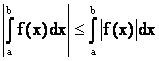 a,b

,    (a < b).