5.2. Интегрирование по частям
Теорема 5.1. (Формула интегрирования по частям для определенного интеграла). Если u = u(x) и v = v(x) непрерывны вместе со своими производными на a,b], то
. (5.2)
Д о к а з а т е л ь с т в о:
Рассмотрим 
тогда
все интегралы существуют,
так как функции непрерывны.
По формуле Ньютона-Лейбница
.
Отсюда следует (5.2).
6. Приложения определенного интеграла
6.1. Площадь плоских фигур
Рассмотрим приложения определенного интеграла для вычисления площадей некоторых плоских областей.
Пусть требуется определить S - площадь криволинейной трапеции, ограниченной графиком функции y = f(x), отрезком a x b и x = a, x = b на основании геометрического смысла определенного интеграла
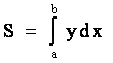, (6.1)
где y = f(х).
Пусть y1 = f1(x), y2 = f2(x) (y2 y1), x = a, x = b. f1(x), f2(x) 0 при x[a,b].
Тогда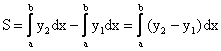 
.
Если f1(x)
= y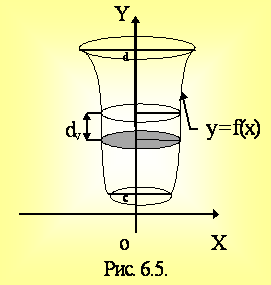
1, f2(x)
= y2
; 
-
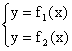решение системы. Тогда так
же имеем
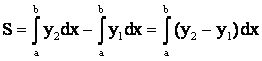
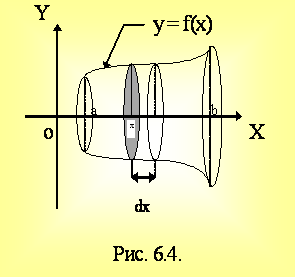. (6.2)
6.2. Объем тела в ращения
Необходимо
определить объем тела Vх,
образованного вращением вокруг оси
Ох криволинейной
т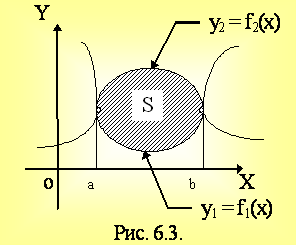
рапеции
y = f(x) (f(x) 0), отрезок a x b.
S(x) = y2, dVx = y2dx
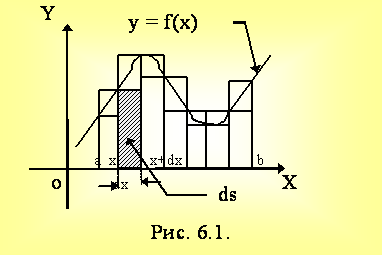. (6.3)
Пусть теперь необходимо определить объем тела Vу, образованного вращением вокруг оси Оу криволинейной трапеции
x = g(y) 0, y = c, y = d
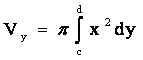. (6.4)
3. Длина дуги
Определение 6.1. Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего ее звена стремится к нулю.
Если кривая непрерывна и в каждой точке имеет касательную, непрерывно меняющую свое положение от точки к точке, то будем называть такую кривую гладкой.
Пусть y = f(x) - гладкая кривая для x[a,b] и f(x) - непрерывна вместе с f/(x) на [a,b].
Теорема 6.1. Каждая гладкая кривая y = f(x) на [a,b] имеет определенную конечную длину дуги.