Рассчет в Mathcad.

Значениям t и h(t) соответствуют столбцы TOUT и SIMOUT(h(t)) взятые из Exсel, примененного в методе последовательного логарифмирования.

Метод моментов.

При использовании метода моментов основной проблемой является нахождение функциональной зависимости между моментом входной и выходной функции.

Получить явные выражения для моментов можно несколькими способами.

Первый способ состоит в решении математической модели. Основным достоинством этого метода является возможность определения моментов как

для линейных, так и для нелинейных операторов, при любом промежутке интегрирования Т. Момент произвольной функции Ф интеграл вида

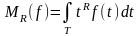
Однако в большинстве случаев получение решения уравнений математической модели в пространстве оригиналов представляет собой довольно сложную задачу. В связи с этим представляют значительный интерес методы, позволяющие определять моменты выходных кривых без предварительного получения решения уравнений модели в пространстве оригиналов. Оказывается, что для вычисления моментов функции достаточно знать ее изображение по Лапласу (которое часто найти гораздо легче, чем функцию). Действительно, согласно определению преобразования по Лапласу функции Ф(t), ее изображение

Это равенство при p=0 имеет вид

, т.е.

Найдем значение

Аналогично, для производных более высокого порядка получим:

Таким образом, для получения момента любого порядка некоторой функции Ф(t) достаточно продифференцировать по р необходимое число раз изображение 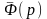этой функции и положить р=0.

Наша передаточная функция описывается уравнением апериодического звена второго порядка. Ее изображение по Лапласу имеет вид:

Тогда выражение примет вид:

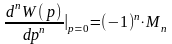
Рассчитаем нулевой момент:

Рассчитаем первый момент (математическое ожидание):

С другой стороны, т.к. математическое ожидание – это среднее арифметическое значений импульсной переходной функции k(t)=C₀-h(t)

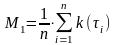
Рассчитаем второй момент (дисперсию):

С другой стороны, т.к. дисперсия – это квадрат отклонения значений k(t) от среднего арифметического M₁ .

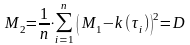
Итак, получившаяся система уравнений позволяет найти T₁ и T₂, а следовательно и α₁ и α₂ .

Расчёт в среде MathCad.

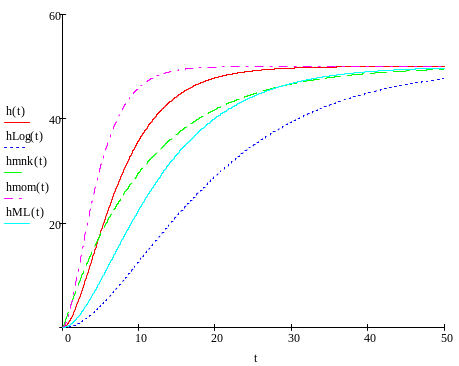
Выбор наиболее адекватной модели объекта:

	Log	MNK	MOM	ML(ident)
D	333.5145	278.158	57.603	2276
SKO	18.26238	5.34	7.59	47.71
T1	8.3	11.048	2.574	8.3327
T2	12.165	0.104	2.272	4.998
K	50	50	50	50

Вывод: в итоге, наиболее приближенной является функция, полученная методом МНК, т.к. среднее квадратическое отклонение у неё самое маленькое. В дальнейших расчетах будем использовать её.