Функции нескольких переменных

1. Линии уровня. Поверхности уровня

Определение: Если любой упорядоченной паре чисел из некоторого числового множества поставлено в соответствию по некоторому правилу f число z из множества Z, то говорят, что на множестве D задана функция .

х и у – независимые переменные (аргументы),

z – зависимая переменная (функция),

- область определения функции,

- множество значений функции.

Каждой упорядоченной паре чисел соответствует единственная точка М плоскости Оху.

Аналогично можно определить функцию любого конечного числа независимых переменных

Геометрическим изображением функции в прямоугольной системе координат является некоторая поверхность.

Определение: Линией уровня функции называется линия на плоскости .

В каждой точке, лежащей на этой линии, функция принимает значение равное с.

Пример. Построить линии уровня функции для .

1. - гипербола

2. 

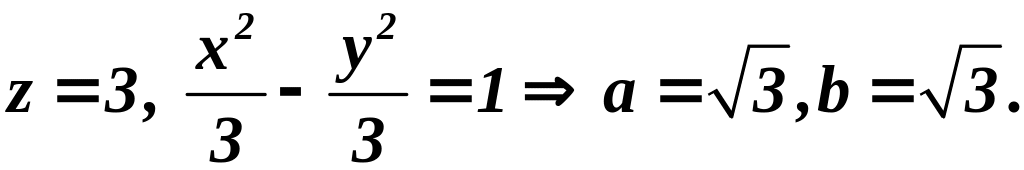
Определение: Поверхностью уровня называется поверхность в точках которой функция сохраняет значение, равное с.

Пример. Построить поверхности уровней для функции при

- это точка,

- это сфера,

2. Частные производные функции. Производная по направлению. Градиент

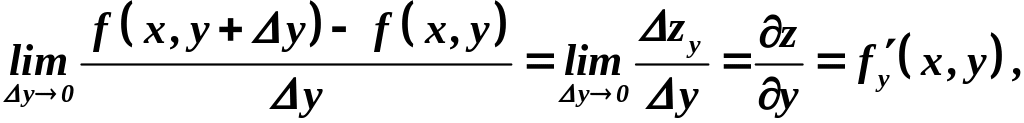Определение: Частной производной от функции по независимой переменной x называется конечный предел вычисленный при постоянном значении у. Частной производной по у называется конечный предел: вычисленный при постоянном значении х.

Для вычисления данных производных можно воспользоваться обычными правилами и формулами дифференцирования.

Пример. Показать, что функция удовлетворяет уравнению

Находим частные производные

Подставим все в уравнение:

Т.е. удовлетворяет уравнению.

Пусть определена в некоторой окрестности точки Пусть вектор - единичный вектор, задающий направление прямой L, проходящий через точку Выберем на прямой L точку Рассмотрим приращение функции в точке М.

О пределение: Предел отношения если он существует, называется производной функции в точке по направлению вектора и обозначается Если функция имеет в точке М непрерывные частные производные, то в этой точке любая производная по каждому направлению, исходящему из точки и она равна:

где - направляющие косинусы вектора

Пример. Вычислить производную функции в точке в направлении вектора

Решение:

1. Находим единичный вектор

2. Находим частное производные в точке М

Тогда

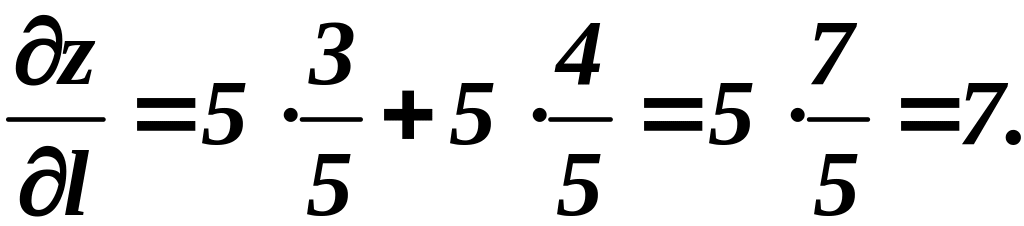
Определение: Градиентом функции в точке называется вектор с началом в точке координаты которого равны соответствующим частным производным, вычисленном в точке, т.е.

Градиент есть вектор, указывающий направление наибольшего возрастания функции.

Аналогично, для случая трёх переменных

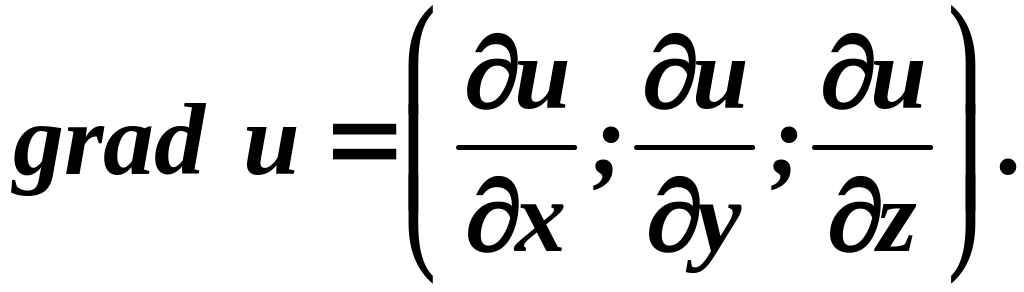
Пример. Найти

в точке

Решение:

Имеем:

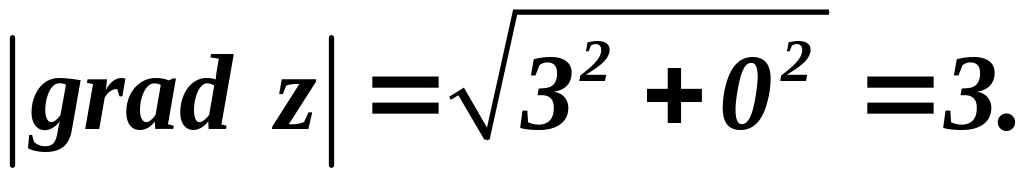
3. Дифференциал. Частные производные высших порядков

Определение: Дифференциалом дифференцируемой функции в точке М называется главная линейная относительность и часть полного приращения этой функции.

Пусть функция имеет первые частные производные.

Определение: Частные производные от частных производных называются частными производными II порядка от функции в точке М.

Обозначается:

Аналогично определяются и обозначаются производные III и более высокого порядков:

Если первые частные производные непрерывны, то можно вычислить «смешанную» производную: сначала вычисляем частную производную по х, а потом эту производную дифференцируем по у, т.е.

Пример.

Дана:

Найти

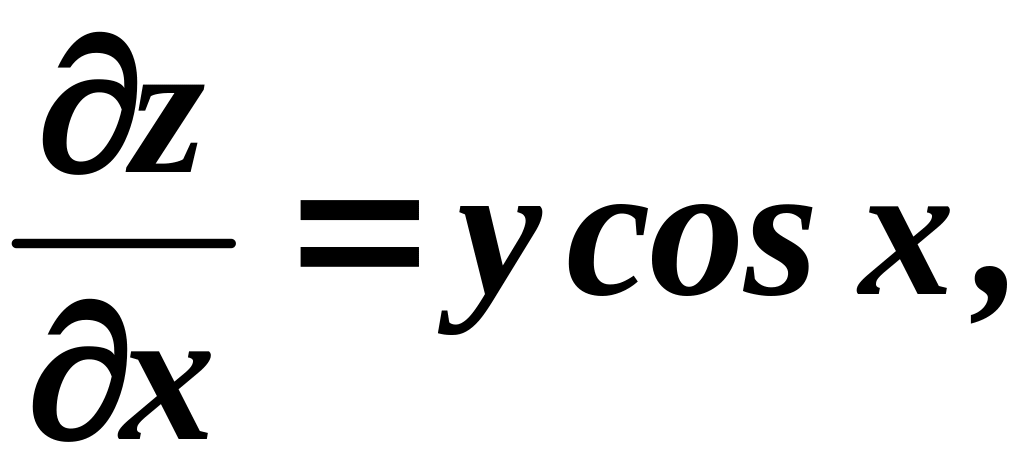
Найти вторые частные производные и вторую смешанную частную производную.