2.1.1. Векторный способ задания движения

Если точка М перемещается относительно выбранной системы отсчета с неподвижным центром в точке О, то ее положение (рис. 2.1) относительно фиксированной точки О системы отсчета будет полностью определено, если в каждый момент времени будут известны модуль и направление ее радиус-вектора относительно точки О. Таким образом, движение точки М задается векторной функцией

. (2.1)

Это равенство называется векторным уравнением движения или законом движения точки в векторной форме.

О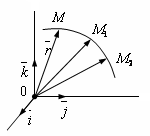 чевидно, что траектория точки М представляет собой геометрическое место точек концов радиус-вектора движущейся точки.

Из векторного исчисления известно, что линия, образованная концами

Рис. 2.1 переменного вектора, начало которого находится в определенной точке пространства, называется годографом этого вектора. Следовательно, траектория точки М является годографом ее радиус-вектора .

2.1.2. Координатный способ задания движения

И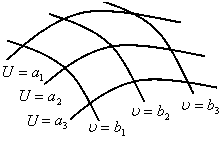 з аналитической геометрии известно, что положение любой точки на плоскости или в пространстве может быть определено при помощи той или иной системы координат. Наиболее общая система координат – координатная.

Рис. 2.2 1. На плоскости задаются два семейства координатных линий зависящих каждое от одного параметра, причем через каждую точку проходит только одна линия каждого семейства (рис. 2.2). Значения параметров, соответствующие этим кривым, являются криволинейные координаты .

2. В пространстве задаются три семейства координатных поверхностей, таких, что через каждую точку пространства проходит по одной поверхности каждого семейства. Положение точки в такой системе определяется значениями параметров координатных поверхностей, проходящих через эту точку.

Частные, наиболее употребительные системы координат: прямоугольная декартова, цилиндрическая, сферическая, полярная и др.

2.1.3. Движение точки в декартовой системе координат

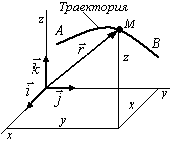Пусть точка О является началом прямоугольной системы координат Oxyz , и пусть - соответственно единичные векторы осей (рис. 2.3). Тогда радиус-вектор точки М относительно начала отсчета - точки О может быть выражен через его проекции на оси x, y, z

. (2.2)

Модуль и направление радиус-вектора будут

Рис. 2.3 определены, если в каждый момент времени известны координаты точки, т.е. заданы три равенства

, , . (2.3)

Рис.7

Эти три функции называются уравнениями или законом движения точки в координатной форме. Если точка движется в плоскости, то имеем два уравнения

, . (2.3*)

Уравнения (2.3) и (2.3*) представляют собой параметрические уравнения траектории точки М, в которых роль параметров играет время t. Чтобы получить уравнения траектории в координатной форме в виде зависимости только между координатами точки М, надо из них исключить параметр t.

Пример. Движение точки задано уравнениями

, .

Найти траекторию точки.

Р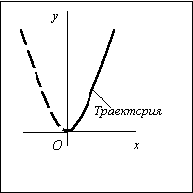 е ш е н и е . Определим уравнение траектории, исключив время t из заданных уравнений движения:

t = х у = х²_. Полученная кривая является параболой, проходящей через начало координат и имеющей осью симметрии ось Оу (рис. 2.4) Так как интервал времени в задаче не задан, примем,

Рис. 2.4 что время меняется в преде-лах от нуля до бесконечности. Тогда из уравнений движения получаем пределы изменения координат точки:

если 0 ≤ t < ∞, то 0 ≤ х < ∞, 0 ≤ у < ∞.

Таким образом, в процессе движения координаты точки остаются положительными, следовательно, траекторией точки будет только правая часть параболы (на рис. 2.4 она изображена сплошной линией).