13.3. Дифференциальные уравнения первого порядка

Определение. Дифференциальным уравнением первого порядка называется уравнение вида

F (x, y, y) = 0, (13.3)

где х  независимая переменная, у  искомая функция, у   ее производная. Если уравнение (13.3) можно разрешить относительно у, то оно принимает вид

у = f (x, y) (13.4)

и называется уравнением первого порядка, разрешенным относительно производной.

Общее решение уравнения (13.3) имеет вид

у = φ (х, С) или Ф (х, у, С) = 0,

а частное решение

у=φ (х, С₀) или Ф (х, у, С₀)=0,

где С₀ определяется из начальных условий задачи Коши: у(х₀)=у₀.

Г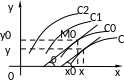 еометрически общее решение у = φ (х, С) представляет собой семейство интегральных кривых на плоскости хОу, зависящее от одной произвольной постоянной С, а частное решение у = φ (х, С₀)  одну интегральную кривую этого семейства, проходящую через заданную точку (х₀, у₀) (см.рис.).

Таким образом геометрически задача Коши формулируется так: из семейства интегральных кривых уравнения (13.4) найти одну интегральную кривую, проходящую через точку М₀(х₀, у₀).

Т е о р е м а К о ш и (существования и единственности решения задачи Коши). Если функция f(x, y) и ее частная производная 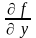определены и непрерывны в некоторой области плоскости хОу и, следовательно ограничены в ней, то какова бы ни была внутренняя точка (х₀, у₀) этой области, в некоторой окрестности этой точки существует единственное решение задачи Коши:

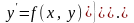
Определение. Решение, в каждой точке которого нарушается единственность или существование решения задачи Коши, называется особым (геометрически: совокупность точек плоскости, через которые либо проходит более одной интегральной кривой, либо не проходит ни одной интегральной кривой, называется особыми точками данного уравнения).

Не существует общего метода интегрирования дифференциального уравнения первого порядка. Обычно рассматривают лишь некоторые отдельные типы таких уравнений, для каждого из которых дается свой особый способ решения.

Дифференциальные уравнения с разделяющимися переменными

Определение. Дифференциальное уравнение вида

X (x) d x + Y (y) d y = 0 (13.5)

называется уравнением с разделенными переменными.

Считая y = φ(x) известной, это уравнение можно рассматривать как сумму двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным числом. То есть общий интеграл уравнения (13.5) имеет вид:

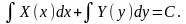
Определение. Уравнение вида

X₁(x) Y₁(y) d x + X₂(x) Y₂(y) d y = 0 (13.6)

называется уравнением с разделяющимися переменными.

Уравнение с разделяющимися переменными может быть приведено к уравнению (13.5) путем деления обеих частей уравнения на произведение Y₁(y)·X₂(x):

Замечание. Уравнение у = f₁(x) f₂(y) приводится к уравнению (13.5) следующим образом

,

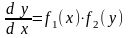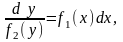
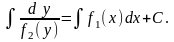
Решение f₂(y) = 0 может быть особым.

Дифференциальные уравнения однородные относительно переменных

Определение. Функция f (x, y) называется однородной функцией п – го измерения относительно переменных х и у, если при любом k справедливо тождество: f (kx, ky) = k ⁿ f (x, y).

Определение. Функция f (x, y) называется однородной функцией нулевого измерения, если при умножении аргументов х и у на произвольный параметр k значение функции не измениться: f (kx, ky)= f(x,y).

Определение. Уравнением однородным, относительно переменных называется уравнение вида:

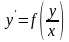(13.7)

При решении однородного уравнения вводится замена

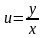, т. е. y = u∙x,

тогда у = u x + u, подставляя это выражение для у в однородное уравнение, получим:

u x + u = f (u)

или u x = f (u) – u  это уравнение с разделяющимися переменными:

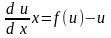
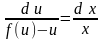
Интегрируя найдем:

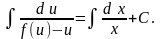
Подставляя после интегрирования вместо U отношение 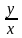, получим интеграл однородного уравнения.

Замечание. Уравнение

М (х, у) d y + N (x,y) d x = 0 (13.8)

будет однородным в случае, если М (х, у), N (x, y) - однородные функции одного и того же измерения.