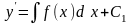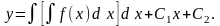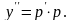13.9. Решение дифференциальных уравнений с помощью рядов.

Если решение дифференциального уравнения нельзя выразить через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближённого решения уравнения можно воспользоваться степенным рядом. Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.

Способ последовательного дифференцирования.

Пусть требуется решить уравнение

у ¢¢ = f (x, y, y¢), (13.20)

решение которого удовлетворяет начальным условиям

y (х₀)= y₀, y ¢(х₀) = y¢₀ (13.21)

Решение данного уравнения найдём в виде ряда Тейлора:

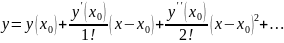
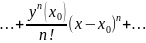(13.22)

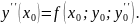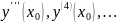В котором первые два коэффициента сразу определяются из начальных условий (13.21). Подставив в уравнение (13.20) значения х = х₀, y = y₀, y ¢ = y¢₀ , находим третий коэффициент Путём последовательного дифференцирования уравнения (13.20) и вычисления производных при х = х₀ найдём значения Найденные значения производных (коэффициентов) подставляем в разложение (13.22), которое представляет искомое частное решение уравнения (13.20) для тех значений х, при которых он сходится. Частичная сумма ряда, стоящего в правой части (13.22) и будет приближённым решением исходного дифференциального уравнения.

Метод неопределённых коэффициентов.

Этот способ приближённого решения удобен для интегрирования линейных дифференциальных уравнений с переменными коэффициентами. Пусть требуется решить уравнение:

у ¢¢ + р (х) у ¢ + q (x) y = f (x), (13.23)

с начальными условиями х = х₀, y = y₀, y ¢ = y¢₀ .

Искомое решение ищем в виде степенного ряда с неопределёнными коэффициентами

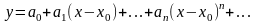(13.24)

предполагая, что функции р (х), q (x) и f (x) разлагаются в сходящиеся к ним степенные ряды.

Коэффициенты а₀ и а₁ находим из начальных условий:

а₀ = y₀, а₁= y¢₀.

Последующие коэффициенты разложения (13.24) находим, дифференцируя равенство (13.24) два раза (каков порядок уравнения) и подставляем выражения для функции у и её производных в исходное уравнение (13.23), заменив в нём р (х), q (x), f (x) их разложениями. В результате получается тождество, из которого определяются недостающие коэффициенты методом неопределённых коэффициентов. Полученный ряд имеет тот же интервал сходимости и служит решением уравнения (13.23)

Сводная таблица по теме: «Дифференциальные уравнения»

№	Вид уравнения	Способ решения
Дифференциальные уравнения первого порядка
1.	Уравнение с разделяющимися переменными X1 (x) Y1(y) d y + + X2(x)∙Y2 (y) d y = 0.	а) X1 (x) Y1(y) d y = X2(x)∙Y2 (y) d y б) .
	y  = f1(x)∙f2(y).	а) , б) с)
2.	Однородное уравнение .	а) Вводится замена , т. е. y = u∙x, б) Получаем у = u x + u. в) подставляем в однородное уравнение: u x = f (u) – u. в) . г) Интегрируя найдем:
3.	Линейное уравнение у + р (х) у = f (x)	а) Введем замену: у (х) = u (x) v (x), тогда у  = u  (x) v (x) + u (x) v  (x). б) Получаем: u ∙v +u∙(v  + p (x)∙v) = g (x). в)
Дифференциальные уравнения второго порядка
4.	Допускающие понижение порядка: 1. у = f (x) не содержит явно у и у .	а) Вводим замену у  = р(х), у = р(х). б) в)
	2. у  = f (x, y ) не содержит явно у.	а) Полагая у  = р (х), у  = р(х), т. е. р = f (x, p) б) р (х) = φ (х, С1). в) Интегрируем и получим
	3. у  = f (y, y ) не содержащим явно х	а) Полагая у  = р (у (х)). Тогда б) Подставляя в уравнение получим р р = f (y, p). в) Решая его, найдем р = φ (у, С1), отсюда . г)
5.	Линейное однородное уравнение у  + р у + q y = 0	Составляем характеристическое уравнение: k^2+ p k + q = 0. Если k1  k2 , то Если k1 = k2, то Если , то
6.	Линейное неоднородное уравнение у  + р у + q y = f (x), f (x) имеет специальный вид	1. Решаем соответствующее однородное уравнение у  + р у + q y = 0 2. По виду правой части уравнения записывается форма частного решения с неопределенными коэффициентами. 3. Таким образом сформированное частное решение подставляется в дифференциальное уравнение. 4. Из полученного тождества определяются значения коэффициентов. 5.
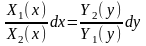