Линейные дифференциальные уравнения

Определение. Уравнение вида

у + р (х) у = f (x), (13.9)

где р (х) и f (x)  непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Если f (x)  0, то уравнение (13.9) называется линейным однородным уравнением. Если f (x)  0, то уравнение (13.9) называется линейным неоднородным дифференциальным уравнением.

Для нахождения общего решения уравнения (13.9) можно пользоваться следующим способом.

Будем искать решение у (х) уравнения (13.9) в виде

у (х) = u (x)·v (x), (13.10)

где u (x) и v (x) – неизвестные функции, одна из которых, например v (x), может быть выбрана произвольно. Подставляя у (х) в форме (13.10) в уравнение (13.9), учитывая, что у = u (x)·v(x) + u(x)·v (x), получим:

u ∙v + u∙v  + p (x)∙u∙v = g (x).

После элементарных преобразований получим

u ∙v + u∙(v  + p (x)∙v) = g (x).

Выберем в качестве v (x) любое частное решение v (x)  0 уравнения

v  + p (x)∙v = 0,

Тогда u ∙v = g (x).

Итак, решение уравнения (13.9) сводится к решению системы дифференциальных уравнений (сначала решается первое уравнение, затем второе)

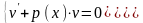
Зная u (x) и v (x), найдем решение у (х) по формуле (13.10) уравнения (13.9).

Уравнение Бернулли

Определение. Уравнение вида

у ¢ + р (х) у = f (x) y ⁿ,

где р(х), f(x)-непрерывные функции от х, а п¹0, п¹1, называется уравнением Бернулли.

Это уравнение приводится к линейному следующим образом

у^-п у ¢ + р (х) у^{-n + 1} = f (x)

Вводится замена z = y ^{– n + 1}. Тогда z ¢ = (– n + 1) y ^{– n} y ¢

Таким образом, получили линейное уравнение относительно функции z

z ¢ + (– n + 1) p (x) z = (– n + 1) f (x).

Получив его общий интеграл и подставив вместо z выражение

у ^{– п + 1}, получим общий интеграл уравнения Бернулли.

Замечание. Решение уравнения Бернулли можно искать и в виде у =u (x)∙v(x) как это описано при решении уравнения (13.9).

13.4. Дифференциальные уравнения второго порядка

Определение. Уравнение вида F (x, y, y, y) = 0 называется дифференциальным уравнением второго порядка или, если это возможно в виде разрешенном относительно старшей производной:

у  = f (x, y, y) (13.11).

Задача Коши для уравнения второго порядка имеет вид

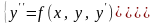(13.12)

Т е о р е м а К о ш и. (существования и единственности задачи Коши). Если функция f (x, y, y) и ее частные производные f_y(x, y, y) и f_y(x, y, y) определены и непрерывны и, следовательно, ограничены в некоторой области пространства переменных (x, y, y), тогда в любой окрестности точки (х₀, у₀, у₀) этой области существует единственное решение уравнения у  = f (x, y, y), удовлетворяющее условиям

y = y₀, y  = y₀ при x = x₀.

Геометрически это означает, что через заданную точку (х₀, у₀) плоскости проходит единственная интегральная кривая с заданным угловым коэффициентом у₀ касательной в точке (х₀, у₀).

Определение. Функция у = φ (х, С₁, С₂) зависящая от х и двух произвольных постоянных С₁ и С₂ и при подстановке в уравнение у = f (x, y. y) обращающая его в тождество называется общим решением этого уравнения.

Геометрически общее решение уравнения второго порядка представляет собой бесконечную совокупность интегральных кривых, зависящую от двух независимых параметров С₁ и С₂.

Определение. Любая функция, получающаяся из общего решения уравнения (13.11) при определенных значениях постоянных С₁ и С₂, т. е. у = φ(х, С₁⁰, С₂⁰) называется его частным решением.

Геометрическое истолкование задачи Коши.

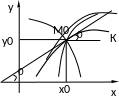
Для того, чтобы из совокупности интегральных кривых выбрать одну, недостаточно указать точку М₀(х₀, у₀), т. к. через нее проходит пучок интегральных кривых. Поэтому, чтобы

из семейства интегральных кривых выделить одну кривую К, следует помимо точки М₀(х₀, у₀) указать направление в котором кривая К проходит через точку М₀, т. е. задать tg ₀ угла образованного касательной к кривой К в точке М₀ и положительным направлением оси Ох, т. е. tg ₀ = у₀. Таким образом постоянные С₁ и С₂ общего решения уравнения (13.11) удовлетворяющего начальным условиям задачи Коши у (х₀) = у₀, у(х₀) = у₀ определяются из системы: