13.5. Уравнения второго порядка, допускающие понижение порядка

I. Уравнение вида у = f (x) не содержит явно у и у .

Вводим замену у  = р(х)  у = р(х) и подставим в уравнение: р = f (x)  уравнение первого порядка. Его решение

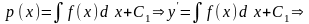
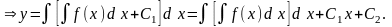
В более общем случае у ^(п) = f (x) решение получается путем п – кратного интегрирования функции f (x), т. е.

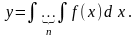
II. Уравнение вида у  = f (x, y ) не содержит явно у.

Полагая у  = р (х), получим у  = р(х) и, подставив в уравнение, получим уравнение первого порядка

р = f (x, p)

с неизвестной функцией р. Решая его найдем функцию р (х) = φ (х, С₁).

Так как р (х) = у , то у  = φ (х, С₁), отсюда интегрируя еще раз получим решение исходного уравнения

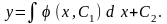
III. Уравнение вида у  = f (y, y ) не содержащим явно х. Вводится новая функция у  = р (у (х)). Тогда

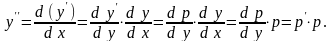
Подставляя в уравнение, получим уравнение первого порядка относительно функции р (как функции от у):

р р = f (y, p).

Решая его, найдем р = φ (у, С₁), т. к. р = у , то у  = φ (у, С), отсюда

.

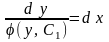В итоге, общий интеграл исходного уравнения имеет вид

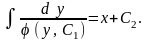
13.6. Линейные дифференциальные уравнения второго порядка

Определение. Линейным дифференциальным уравнением второго порядка называется уравнение первой степени (линейное) относительно неизвестной функции и её производных

у  + р (х) у  + q (x) y = f (x), (13.13)

p (x), q (x), f (x)  непрерывные в некотором интервале [а;в] функции.

Если f (x)  0, то уравнение называется однородным

у  + р (х) у  + q (х) у = 0 , (13.14)

если f (x) ¹ 0 - неоднородным.

Т е о р е м а 13.1. (основное свойство частного решения линейного однородного дифференциального уравнения второго порядка).

Если функции у₁(х) и у₂(х) – частные решения уравнения (13.14), то функция

у = С₁ у₁ (х) + С₂ у₂ (х)

также является решением уравнения (13.14). Это свойство проверяется непосредственной подстановкой у в уравнение (13.14).

Определение. Два решения у₁ и у₂ называются линейно независимыми на отрезке [а;в], если их отношение на этом отрезке не является постоянным, то есть, если 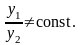В противном случае решения называются линейно зависимыми.

Определение. Если у₁ и у₂ - функции переменной х, то определитель

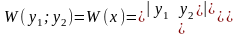
называется определителем Вронского или вронскианом данных функций.

Т е о р е м а 13.2. (об определителе Вронского линейно зависимых функций)

Если функции у₁(х) и у₂(х) линейно зависимы на отрезке [а;в], то определитель Вронского, составленный из них, равен нулю на этом отрезке.

Доказательство. Пусть у₁ и у₂ - линейно зависимы, тогда

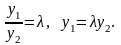
Подставляя в определитель Вронского:

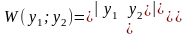
Т е о р ем а 13.3. (об определителе Вронского линейно независимых функций).

Если решения у₁(х) и у₂(х) линейно независимы на отрезке [а;в] решения уравнения (13.14), то определитель Вронского, составленный из них отличен от нуля на этом отрезке.

Т е о р е м а 13.4. (о структуре общего решения уравнения (13.14)). Если у₁(х) и у₂(х) – два линейно независимых решения уравнения (13.14), то функция

у = С₁ у₁ (х) + С₂ у₂ (х)

(С₁, С₂  произвольные постоянные) является общим решением уравнения (13.14).

Т е о р е м а 13.5. (о структуре общего решения неоднородного линейного уравнения второго порядка): Общее решение уравнения (13.13) представляет собой сумму любого его частного решения 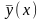и общего решения у₀ соответствующего однородного уравнения, т. е.

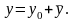
Доказательство. Пусть - частное решение уравнения (13.13), а

у₀ = С₁ у₁ (х) + С₂ у₂ (х)

общее решение уравнения (13.14).

Докажем, что 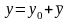- общее решение уравнения (13.13). Для этого покажем, что является решением уравнения (13.13). Найдём

,

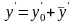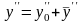
и подставим в (13.13)

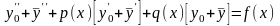
Раскроем скобки и перегруппируем слагаемые

,

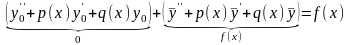
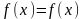следовательно, - решение уравнения (13.13).

Покажем теперь, что оно является общим решением этого уравнения, т.е. докажем, что из решения можно выделить единственное частное решение, удовлетворяющее начальным условиям у (х₀) = у₀, у¢(х₀) = у¢₀.

Продифференцируем функцию 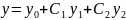и подставим в неё и её производную начальные условия у (х₀) = у₀, у¢(х₀) = у¢₀. Получим систему уравнений с неизвестными C₁ и C₂:

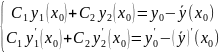
Так как определителем системы является определитель Вронского линейно независимых функций у₁ и у₂ в точке х₀, не равный нулю, то она имеет единственное решение:

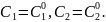Таким образом мы получили частное решение уравнения (13.13)

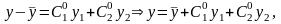
удовлетворяющее заданным начальным условиям. Теорема доказана.

Итак, чтобы найти общее решение уравнения (13.13) надо найти общее решение соответствующего однородного уравнения и какое-нибудь частное решение неоднородного уравнения.

В общем случае задача отыскания частного решения является сложной. Рассмотрим общий метод нахождения частных решений неоднородного уравнения (13.13), когда f (x) – любая функция, если известно общее решение соответствующего однородного уравнения.