Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий. Основная формула комбинаторики Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*...*nk. Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая - из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2. Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n1*n2*n3=6*7*4=168. В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=...nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n^k.Такой способ выбора носит название выборки с возвращением. Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5^4=625. Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью. Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначается An^m и вычисляется по формуле:   Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1. Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет: Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}. Число сочетаний обозначается Cn^m и вычисляется по формуле:   Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся? Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно: Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд? Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг. Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно. Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов). Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны. И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере. Пример. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек? Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5. Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5. Задачи для самопроверки 1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? 2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево? 3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день? 4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек? 5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо? 6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?

Элементы комбинаторики

Комбинаторная математика занимается в основном задачами о существовании и подсчете различных комбинаций, которые можно составить из элементов заданного конечного множества. Эту область математики так назвал Готтфрид Вильгельм Лейбниц в 1666 году в своей диссертации об искусстве комбинаторики, в которой он решает основные комбинаторные задачи, приводящие к биномиальным коэффициентам и к факториалу. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке Паскаль, Ферма, Яков Бернулли и Эйлер, рассматривая азартные игры и всевозможные лотереи. В XVIII - XIX вв. в германских государствах Европы была предпринята попытка создать (Гинденбург, Штейнер, Эшенбах, Роте) комбинаторный анализ как единую науку, чему помешали громоздкость символического аппарата и слабость его оперативно-вычислительных возможностей.

В связи с развитием вычислительной техники резко расширились возможности перебора и повысился интерес к дискретным моделям, что обусловило новый подъем комбинаторной математики. Комбинаторные методы применяются сейчас в теории кодирования, планировании эксперимента, топологии, математической логике, теории игр, кристаллографии, биологии, статистической физике, экономике и т.д.

В нашем случае комбинаторика является основой для изучения теории вероятностей и математической статистики.

1.1. Опорная таблица

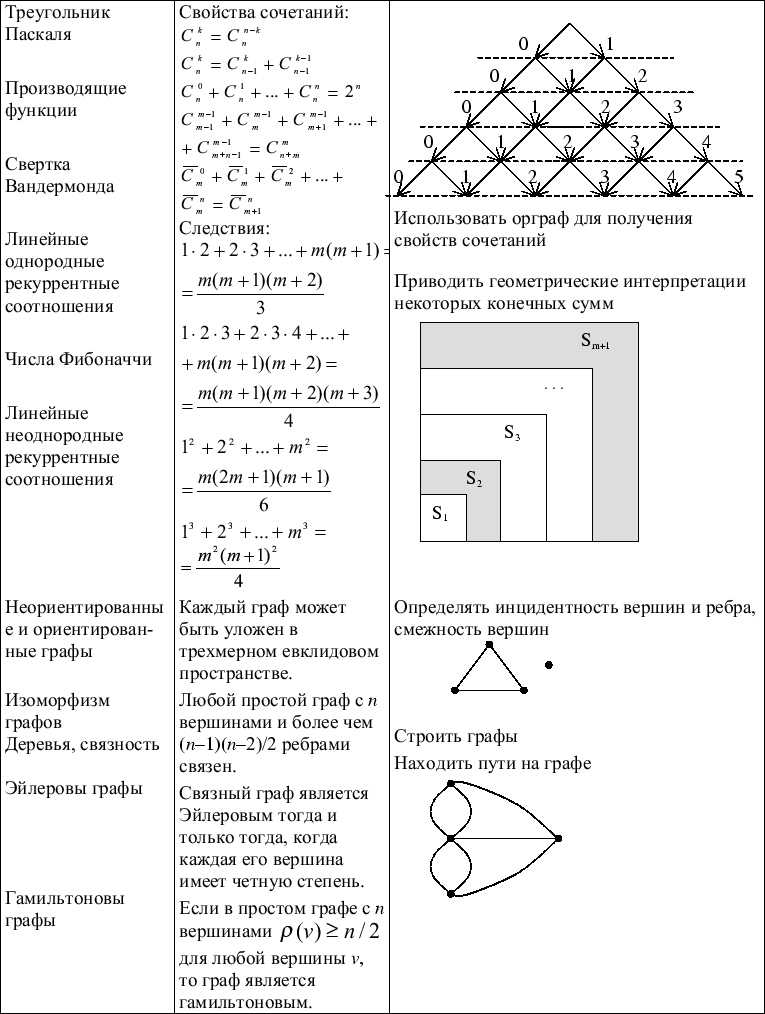
1.2. Методы

1.3. Алгоритмы

Графы

Начало теории графов было положено Эйлером в 1736 году в его знаменитой задаче о кёнигсбергских мостах. Исследования электрических цепей, моделей кристаллов и структур молекул, развитие формальной логики побудили к изучению графов. Большое число популярных головоломок поддавалось формулировкам непосредственно в терминах графов. Проблема четырех красок - наиболее известная среди таких задач - была поставлена Де Морганом в 1850 году. В ХХ столетии теория графов получила дальнейшее развитие, которое связано с новыми ее приложениями: в теории игр и программировании, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем биологии и психологии.

В данной работе графы являются основой для иллюстрации основных результатов в теории вероятностей, что позволяет сделать рассматриваемый материал более наглядным и доступным.

Графом называется два множества с отношением инцидентности между их элементами, называемыми вершинами и ребрами. Это отношение удовлетворяет единственному требованию (аксиоме) - любое ребро инцидентно не более чем двум вершинам.

Пример 16. Построить граф, вершинами которого является множество {2, 3, 4, 5, 6}, а инцидентность задается наличием у указанных цифр делителей, отличных от единицы.

Решение. Взятые цифры обозначим на рисунке кружками, которые соединим отрезками (либо петлями) при наличии общих делителей.

Рис. 1

Этот граф содержит 5 петель - ребра, соединяющие (инцидентные) вершину саму с собой. Вершина "5" - изолированная, а подграф с вершинами {2, 3, 4, 6} является связным. Граф связный, если из любой вершины в любую другую можно "пройти" по ребрам. Циклом называется замкнутый путь из ребер, например, вершины {2, 4, 6} с соединяющими их попарно ребрами. Степенью вершины называется число ребер графа, инцидентных этой вершине.

Пример 17. Сколько различных обедов П.И. Чичиков мог насчитать из блюд, выставленных на столе у П.П. Петуха, если бы на каждый обед выбирать только одно холодное блюдо, одно первое блюдо и одно второе блюдо? На столе у П.П. Петуха на этот раз были выставлены из холодных блюд студень с хреном, свежая икра, свежепросоленная белужина; на первое - уха из стерлядей, щи с грибами; на второе - осетрина жареная, теленок, жаренный на вертеле.

Решение. Каждое блюдо изобразим кружком с первой буквой названия блюда, а соответствие блюд одного обеда - отрезками, соединяющими кружки. Возникает схема (граф), изображенный на рисунке:

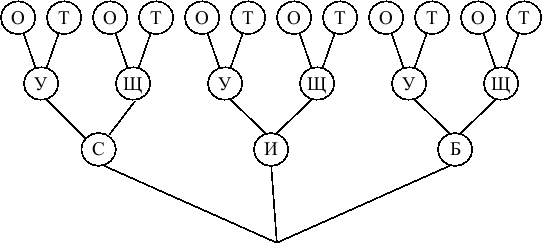
Рис. 2

Граф помогает сосчитать число возможностей, их оказалось 12. Он же помогает узнать, сколько различных обедов можно составить, например, с икрой.

Математики, обратив внимание на сходство схемы на рисунке 2 с веткой дерева с листочками, назвали такие графы "деревьями".

Деревом называется связный граф без циклов. Очень важное понятие для нашего подхода к изложению теории вероятностей. При помощи дерева удобно изображать исходы того или иного испытания.

Пример 18. Поступающий на физмат должен сдать три вступительных экзамена по десятибалльной системе. Сколькими способами он может сдать экзамены, чтобы быть принятым в университет, если проходной балл в тот год составил 28 баллов?

Решение. Для решения этой задачи, как и во многих других комбинаторных и вероятностных задачах, эффективным оказывается организация элементов анализируемого множества в виде дерева. От одной выделенной вершины проводятся ребра, соответствующие оценке на первом экзамене, а затем к их концам добавляются новые ребра, соответствующие возможным результатам второго экзамена, а затем и третьего.

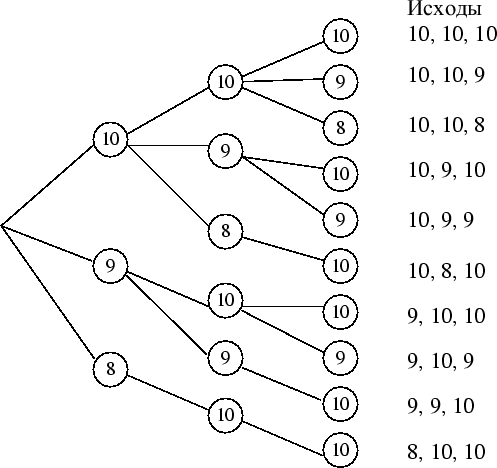
Рис. 3

Таким образом, для поступления на физмат можно сдать вступительные экзамены 10 различными способами.

Из этого представления можно извлечь ряд идей, плодотворных для изучения комбинаторики и вероятности.

При рассмотрении цепей Маркова (далее §11) нам потребуются графы, на ребрах которых поставлены стрелки, указывающие на переход из одного состояния в другое. Ребро графа называется ориентированным, если одну вершину считают началом ребра, а другую - концом. Граф, все ребра которого ориентированы, называется ориентированным графом.

Пример 19. Турнир по волейболу проводится по круговой системе между командами. Докажите, что если какие-нибудь две команды одержали в турнире одинаковое число побед, то найдутся среди участников три команды I, II и III такие, что I выиграла у II, II выиграла у III, a III выиграла у I.

Решение. Пусть и - две команды, одержавшие одинаковое число побед, например, побед. Пусть к тому же выиграла у . Те команд, у которых выиграла команда , обозначим , , ..., (рис. 4).

Рис. 4

Команда не могла одержать победы над всеми командами , , ..., , т.к. иначе она одержала бы больше чем побед (одна победа над уже имеется). Следовательно, среди команд , , ..., найдется хотя бы одна, которая одержала победу над .

Из этого примера следует один из результатов теории графов о существовании ориентированных циклов в полном ориентированном графе.

Граф будет называться вероятностным, если рядом с каждым его ребром запишем соответствующую вероятность.

Пример 20. Построить вероятностное дерево исходов двух подбрасываний монеты на твердую поверхность.

Решение. Поскольку каждое подбрасывание монеты может закончиться одним из двух исходов, а именно, выпадением "герба" или "решки", то вероятностное дерево выглядит следующим образом: