88

1. Элементы теории множеств

1.1. Понятие множества

Понятие множества является базовым в математике, на его основе формируются другие понятия. В силу своей общности – это неопределяемое понятие.

Под множеством принято понимать любое собрание (совокупность) определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами данного множества.

В приведенном выше описании понятия множества, которое принадлежит основателю теории множеств немецкому математику Г. Кантору, существенным является то, что собрание объектов (множество) само рассматривается как один предмет, как нечто целое. Относительно предметов, которые могут входить во множество, допускается значительная свобода. Важно, что наша интуиция должна, во-первых, отделять их один от другого даже тогда, когда их нельзя точно указать (например, множество простых чисел), во-вторых, давать ответ на вопрос о принадлежности объекта данному множеству. Второе тесно связано со способами задания множеств.

Тот факт, что объект а является элементом множества А, другими словами, а принадлежит множеству (содержится в множестве) А, символически обозначается: а А. В противном случае пишут аА.

Г. Кантор сформулировал несколько интуитивных принципов, которые естественно считать выполняющимися для произвольных множеств. В частности интуитивный принцип объемности, который оговаривает условия равенства (тождественности) объектов нашей теории, а, следовательно, и их различия.

Интуитивный принцип объемности. Множества А и В считаются равными, если они состоят из одних и тех же элементов.

При этом записывают А=В, если А и В равны, и АВ – в противном случае.

Пример 1. Пусть множество А состоит из чисел 1 и 6, а В – множество действительных корней уравнения х²–7х+6=0. Числа 1, 6 и только они являются корнями данного уравнения, следовательно, в силу принципа объемности заключаем, что множества равны, т. е. А=В.

Множество А, элементами которого являются объекты а₁ ,а₂, ..., а_n и только они, обозначают А={а₁, а₂, ..., а_n}.

1.2. Отношение включения

Если каждый элемент множества А одновременно является элементом множества В, то А называют подмножеством множества В, и пишут АВ. При этом множество В называют надмножеством множества А. Если АВ, но А В, то А называют собственным подмножеством В, и обозначают АВ. Ясно, что для любых множеств А, В, С справедливо:

0. АА;

1. если АВ, ВС, то АС;

2. если АВ, ВА, то А=В.

Таким образом, равенство двух множеств А и В равносильно двум включениям: АВ, ВА (А=В  АВ, ВА). Это используется при доказательстве равенства множеств.

Нужно различать отношения принадлежности () и включения ( ). Если множество А={а₁, а₂, ..., а_n}, то а₁А, но а₁А, т.к. а₁ не является подмножеством А. Однако, если ввести в рассмотрение множество А₁, состоящее из одного элемента а₁, А₁={а₁}, то А₁А или {а₁}А.

Множество, не содержащее элементов, называют пустым множеством и обозначают .

Например, множество действительных корней уравнения х²+1=0 является пустым множеством. Этот простой пример иллюстрирует целесообразность введения понятия пустого множества.

Пустое множество – подмножество любого множества, т.е. А для любого множества А. Заметим, что множество С={} не является пустым, так как оно содержит элемент – .

Сами множества могут быть элементами других множеств. Если А={а₁, а₂}, В={b₁, b₂}, то D={A, B} не содержит, например, в качестве элементов а₁ или b₁ , т.е. а₁ D , но АD, ВD.

Для множества А = {a,b} рассмотрим все его подмножества: , {a}, {b} и {a, b}. Тогда множество S(A)= {, {a}, {b}, {a, b}} представляет собой «множество всех подмножеств» исходного множества А. Аналогично, для любого множества А можно определить множество всех его подмножеств S(A), которое принято называть булеаном множества А или его степенью.

Если множество А состоит из n элементов (обозначается: |A| = n), то

|S(A)|=2ⁿ . В частности, || = 0, |S()| = |{}| = 2 ⁰ =1.

Множество, элементами которого являются все возможные множества, принято называть универсальным множеством (универсумом) и обозначать U. Таким образом, считают, что для любого множества А справедливо: АU. Однако на практике в качестве универсального множества выбирают подходящее для данной задачи множество U. Например, если решается геометрическая задача, в которой рассматриваются только многоугольники, то имеет смысл в качестве универсального множества U выбрать

множество всех многоугольников.

1.3. Способы задания множеств

Все непустые множества, можно разделить на конечные, которые содержат конечное число элементов, и бесконечные, которые таковыми не являются. Простейший способ задания множества – это перечисление всех его элементов (точнее, “имен” этих элементов). Например, список студентов учебной группы. Очевидно, что этим способом можно задать только конечные множества. Например, множество А – всех целых чисел на отрезке [1,3] конечно, его можно задать перечислением А = {1,2,3}. Множество В – всех рациональных чисел этого отрезка задать перечисление нельзя, так как оно бесконечно.

Рассмотрим способы задания множеств, которые применимы к любым множествам. Множество можно задать с помощью порождающей процедуры, т. е. указать правило, по которому из каких-то объектов строятся элементы данного множества. Например, множество натуральных чисел N можно задать с помощью следующей порождающей процедуры:

1. 1N,

2. 2) если х  N, то х+1 N.

Общепринятая запись: N={1, 2, ..., n, ...} не является заданием множества N перечислением.

Еще одним способом задания множеств является задание множества с помощью характеристического свойства его элементов. Свойство, которым обладают элементы множества А и только они, называется его характеристическим свойством. Более точно этот способ задания можно описать, используя интуитивное понятие «формы от х». Под «формой от х» принято понимать конечную последовательность, состоящую из слов и символа х, такую, что если каждое вхождение символа х заменить одним и тем же именем некоторого предмета, то в результате получится истинное или ложное предложение. Например, формами от х будут предложения: «5 делит х», «х – родственник Иванова». Напротив, предложения «х²–4=(х–2)(х+2) для всех х» или «существует такое х, что х>0» не являются формами от х. Форму от х обозначим через Р(х).

Интуитивный принцип абстракции. Любая форма Р(х) определяет некоторое множество А, а именно множество тех и только тех предметов а, для которых Р(а) – истинное предложение.

Запись А={x| P(x)}означает, что множество А определяется формой Р(х).

Например,

1) А={x|x – целое положительное число, меньшее 5}={1,2,3, 4};

2) А={x| x – буква русского алфавита, входящая в слово «мама»}={а, м};

3) А={x| x = 2n, nN} – множество четных натуральных чисел.

1.4. Операции над множествами

Рассмотрим операции над множествами, которые представляют собой ряд правил, позволяющих получать новые множества из уже заданных.

Определение 1 Объединением (суммой) двух множеств А и В называется множество АВ, состоящее из тех и только тех элементов, которые являются либо элементами множества А, либо элементами множества В:

АВ={x| xA или xВ}.

Другими словами, в объединение АВ входят все элементы как множества А, так и множества В, и других элементов нет. При этом всегда: ААВ , В  А В.

Под объединением любой совокупности множеств будем понимать новое множество, каждый элемент которого является элементом некоторого множества из данной совокупности, при этом, любой элемент каждого множества совокупности есть элемент объединения. В частности, для совокупности множеств: А ₁, А ₂, ..., А _n, ... имеем

Определение 2 Пересечением множеств А и В называется множество АВ, состоящее из тех и только тех элементов, которые являются как элементами множества А, так и элементами В.

АВ ={x| xA и хВ}.

Другими словами, в пересечение АВ входят те и только те элементы множества А, которые входят в В. Если ни один элемент множества А не является элементом множества В, то АВ=. В этом случае говорят, что множества А и В не пересекаются. Ясно, что всегда справедливы включения: АВА, АВВ.

Для произвольной совокупности множеств под пересечением будем понимать новое множество, состоящее из тех и только тех элементов, которые входят во все множества данной совокупности. В частности, для совокупности множеств: А ₁, А ₂, ..., А _n, ... имеем

Определение 3 Разностью двух множеств А и В называется множество А\В, элементами которого являются те и только те элементы множества А, которые не принадлежат множеству В:

А\В={x| xA, но хВ}.

Определение 4 Cимметрической разностью множеств А и В называется множество АВ = (А\B)(B\A).

Другими словами, это множество состоит из тех и только тех элементов А и В, которые не входят в пересечение этих множеств.

Упражнение 1. Доказать, что АВ = (АB)\(АВ).

Пример 3. Пусть А = {1, 2, 3, а, b}, B = {а, b, c, 0, 1, 5}.Найти: АВ, АВ, А\B,В\А, АВ.

Согласно определениям 1 – 4: АВ={0, 1, 2, 3, 5, а, b, с}, АВ={1, a, b}, А\B={2, 3, c}, B\A = {c, 0, 5}, АВ={0, 2, 3, 5, c}.

Определение 5 Дополнением множества А называется множество всех тех элементов, которые не принадлежат А:

.

Если U – универсальное множество, то А = U\A.

Разность Х\А={x| xX, xA }, т.е. множество всех элементов Х, которые не принадлежат А, иногда называют относительным дополнением множества А до множества Х. Отметим, что Х \ A = X А.

Для наглядного представления отношений между подмножествами универсального множества используют диаграммы Эйлера – Венна. Само универсальное множество U изображают в виде прямоугольника, а его подмножества – в виде кругов, расположенных внутри прямоугольника.

На рисунке 1 представлены диаграммы Эйлера – Венна, иллюстрирующие операции над множествами:

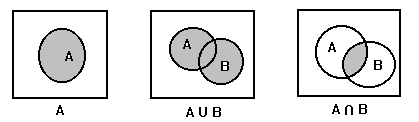
Рис. 1.

Сформулируем основные свойства операций объединения, пересечения и дополнения множеств.

Для любых подмножеств А, В, С и универсального множества U выполняются следующие тождества:

Коммутативность:

1. АВ = ВА; 1. АВ = ВА.

Ассоциативность:

2. А(ВС) = (АВ)С; 2. А(ВС) = (АВ)С.

Дистрибутивность:

3. А(ВС) = (АВ)(АС); 3. А(В С) = (АВ)(А С).

Действия с константами:

4. А = А, А  U = U; 4. А = , АU = А.

5. ; 5. .

Идемпотентность:

6. АА = А; 6. АА = А.

Законы де Моргана:

7. 7. .

Законы поглощения:

8. А(АВ) = А; 8. А(АВ) = А.

Закон двойного дополнения:

9. .

В качестве примера приведем доказательства тождеств 3 и 7.

Доказательство тождества 3. А(ВС) = (АВ) (АС).

Введем обозначения: М = А(ВС) и N = (АВ)(АС). Тогда M=N  МN, NM.

Сначала докажем, что МN. Пусть хМ=А(ВС). Это означает, что а) хА или б) хВС. В случае а) из того, что хА, следует хАВ и хАС, т.е. х(АВ)(АС)=N. Если же хВС, то это означает, что хВ и хС. Следовательно, хВА и хСА, т.е.и в случае б) х(АВ)(АС)=N. Первое включение доказано.

Покажем, что NM. Пусть хN=(АВ)(АС), тогда хАВ и хАС. Следовательно, либо хА, и тогда очевидно, что х А(ВС), либо х А, тогда хВ и х С, т.е. хВС, а значит х А(ВС) = М.

Доказательство тождества 7. .

Пусть . Тогда хАВ. Следовательно, хА и хВ. Это означает, что , т.е. . Итак, . Пусть теперь . Тогда и , следовательно, хА, хВ. Значит, хАВ, т. е. . Итак, . Тождество 7 доказано.

1.5. Эквивалентность множеств. Понятие мощности

Как мы уже отмечали ранее все непустые множества делятся на конечные и бесконечные. Действительно, для некоторых множеств можно точно указать число элементов, содержащихся в данном множестве. Например, для множества всех вершин некоторого многогранника. Для других множеств мы принципиально можем утверждать, что они конечны, хотя фактически указать число элементов не в состоянии. Например, число берез на Земле. С другой стороны, существуют множества, состоящие из бесконечного числа элементов. Например, множество всех натуральных чисел, множество всех точек прямой, множество всех кругов на плоскости. Любое, бесконечное в нашем представлении множество, можно охарактеризовать тем, что, удаляя из него любое конечное число элементов, мы не сможем его исчерпать, т. е. в нем при этом всегда останутся элементы.

Любые два конечных множества можно сравнить по числу содержащихся в нем элементов. Можно ли подобным образом сравнивать бесконечные множества? Имеет ли смысл, например, вопрос о том, чего больше: кругов на плоскости или рациональных точек прямой?

Чтобы сравнить между собой два конечных множества, можно, во-первых, сосчитать число элементов в каждом из них; во-вторых, установить взаимно однозначное соответствие между элементами этих множеств, т.е. каждому элементу одного множества сопоставить один и только один элемент другого множества, и обратно. Очевидно, что взаимно однозначное соответствие между двумя конечными множествами можно установить тогда и только тогда, когда число элементов в этих множествах одинаково.

Метод подсчета числа элементов для сравнения бесконечных множеств очевидно не пригоден, но в силу последнего замечания в основу сравнения таких множеств можно положить метод установления взаимно однозначного соответствия между ними.

Простейшим среди бесконечных множеств является множество натуральных чисел.

Бесконечное множество А называется счетным, если между ним и множеством натуральных чисел N можно установить взаимно однозначное соответствие. Другими словами, элементы множества А можно перенумеровать числами натурального ряда, т. е. А={a₁, a₂, ..., a_n, ...}. Бесконечные множества не исчерпываются счетным, те из них, которые не являются счетными называются несчетным. Приведем примеры счетных множеств.

Пример 4. Множество целых чисел Z={...,–n, ...,–1,0,1,2,..., n, ...} является счетным множеством. Действительно, соответствие, которое каждому неотрицательному числу n0 ставит в соответствие нечетное натуральное число 2n+1, а отрицательному числу n0 – четное число 2|n| , является очевидно взаимно однозначным между множествами Z и N.

Пример 5. Множество С={x| x=2ⁿ, nN} – всех положительных степеней двойки счетное, так как между множеством С и множеством натуральных чисел N существует взаимно однозначное соответствие: 2ⁿn.

Пример 6. Множество рациональных чисел Q={x| x=n/m; nZ, mN} счетно.

Каждое рациональное число х однозначно представимо в виде несократимой рациональной дроби x = n/m. Сумму |n| + m назовем высотой числа х. Ясно, что дробей, имеющих заданную высоту p, конечно. Если нумеровать рациональные числа по возрастанию высоты, то каждое число получит свой номер, т.е. будет установлено взаимно однозначное соответствие между множествами рациональных и натуральных чисел.

Сформулируем некоторые общие свойства счетных множеств.

0. Всякое непустое подмножество счетного множества конечно или счетно.

1. Объединение конечного или счетного множества счетных множеств само является счетным множеством.

2. Всякое бесконечное множество содержит счетное подмножество.

Определение 6 Два множества А и В называются эквивалентными (АВ), если между ними можно установить взаимно однозначное соответствие.

Ясно, что: