4. Элементы теории графов.

Теория графов, как раздел дискретной математики, имеет многочисленные предметные интерпретации. Не случайно она «открывалась» независимо несколько раз, к этому приводили потребности практики. Началом теории графов принято считать решение Эйлером в 1736 году задачи о кенигсбергских мостах. При этом он нашел критерий существования в графе специального маршрута (эйлеров цикл). В середине 19 века инженер-электрик Крихгоф, исследуя электрические цепи, разработал теорию специальных типов графов (деревьев). А математик Кели в 1857 году, занимаясь чисто практическими задачами органической химии, открыл важный класс графов, называемых деревьями и решил перечислительные задачи для трех типов деревьев. К появлению новых понятий и серьезных результатов в теории графов привели попытки решения знаменитой «проблемы четырех красок», которая появилась в это же время. В 20 веке психолог Левин фактически использовал графы для описания «жизненного пространства» индивидуума, эта идея нашла приложения в других психологических исследованиях. Физики-теоретики для «внутренних» нужд своей науки «открывали» теорию графов не один раз. Сам термин «граф» появился в 1936 году в книге венгерского математика Кенига.

Родившись из решения головоломок и занимательных задач, теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Ее с полным основанием можно считать разделом прикладной математики. Областями применения теории графов в настоящее время являются: теория игр и программирование, теория передачи сообщений, электрических и контактных сетей, теория проектирования интегральных логических схем, схем управления, теория автоматов, экономика и статистика, биология, химия, психология, теория расписаний, дискретная оптимизация.

4.1. Основные понятия.

Определение 1 Граф G – это пара множеств, =<V, E>, где V – произвольное непустое множество, элементы которого принято называть вершинами, а E – множество неупорядоченных пар различных вершин, которые называются ребрами.

Пусть V = {v₁, ..., v_n} – конечное множество вершин, |V| = n – число вершин графа G, и Е = {(v_i,v_j) | v_i,v_j  V и v_i  v_j}, |E| = m – число ребер графа G. Тогда G называется (n, m)-графом (заметим, что (v_i,v_j) = (v_j,v_i), так как по определению рассматриваются неупорядоченные пары вершин).

В силу определения 1 множество ребер Е графа G является подмножеством декартова квадрата множества V (ЕVV), т.е. представляет собой бинарное отношение на множестве V. Причем это отношение нерефлексивное и симметричное, так как по определению (v,v)E и рассматриваются неупорядоченные пары вершин. Обратно, произвольное непустое множество V с заданным на нем нерефлексивным, симметричным бинарным отношением Е удовлетворяет определению 1, т.е. представляет собой граф G = <V, E>.

Таким образом, мы установили связь между графами и классами отношений на конечных множествах и фактически пришли к эквивалентному определению графа:

графом G называется непустое множество V, на котором задано нерефлексивное, симметричное бинарное отношение ЕVV.

Если в определении графа рассматривать упорядоченные пары вершин ((v_i,v_j)  (v_j,v_i) при i  j), то получим понятие ориентированного графа или орграфа. В орграфе вершина v₁ называется началом, v₂ – концом ребра е=(v₁,v₂)E, а сами ребра называются дугами. Орграфом, например, можно описать отношение подчиненности между структурными подразделениями некоторой организации.

Кроме того, встречаются следующие обобщения понятия графа. Если допустить, что множество ребер Е содержит одинаковые ребра, которые принято называть кратными или параллельными ребрами, то прейдем к понятию графа с кратными ребрами или мультиграфа. Если ребро е в мультиграфе G встречается k раз, то число k называется кратностью ребра е. Например, таблицу командного розыгрыша можно описать мультиграфом, вершинами которого являются команды, при этом вершины соединяются ребром, если соответствующие команды провели между собой встречу.

Мультиграф, в котором допускаются кратные ребра вида (v,v) (петли), называется псевдографом.

Определение 2 Бинарное отношение Е на множестве вершин графа G=<V, E> называется отношением смежности. Если (v,u)E, то вершины v, uV называются смежными.

С каждым графом, кроме отношения смежности вершин, можно связать еще два бинарных отношения: отношение инцидентности на VE и отношение смежности на множестве ребер Е.

Определение 3 В графе G = <V, E> вершина vV и ребро еЕ называется инцидентными, если е=(v,w) (или е=(w,v)) для некоторой вершины wV.

Ясно, что вершина w в определении 3 также инцидентна ребру е.

Определение 4. Два ребра е₁ и е₂ в графе G = <V, E> называются смежными, если они инцидентны одной и той же вершине vV, т.е. если е₁=(v,u), е₂=(v,w).

Важной числовой характеристикой в графе является понятие степени вершины

Определение 5. Степенью вершины v графа G = <V, E> называется число (v) равное числу ребер, инцидентных этой вершине.

Вершина v графа G называется изолированной, если (v)=0, и концевой (висячей), если (v)=1.

Докажем два простых, но важных факта о степенях вершин произвольного графа.

Теорема 1. Сумма степеней всех вершин графа G=<V,E> является четным числом, оно равно удвоенному числу ребер, т.е.

.

Доказательство. Доказываемое равенство следует из того, что каждое ребро e=(v,w) учитывается при подсчете степени вершины v и при подсчете степени вершины w, т. е. входит в сумму дважды.

Следствие. В любом графе число вершин нечетной степени четно.

Доказательство. Пусть V₁ – множество вершин нечетной степени, а V₀ множество вершин четной степени графа G = <V, E>. Тогда V = V₁V₀ и V₁V₀ = , следовательно,

.

Ясно, что – четное число (k – целое число), а так как , то .

Определение 6 Граф Н=<V₁, E₁> называется подграфом графа G=<V,E>, если V₁V и Е₁Е. Если V₁=V, то подграф Н называется остовным подграфом.

Ясно, что остовной подграф получается удалением некоторых ребер исходного графа.

Определение 7. Граф Н=<V₁, Е₁> называется подграфом, порожденным множеством вершин V₁ (V₁  ) графа G=<V,E>, если любые две вершины v и w из V₁, смежные в графе G, являются смежными в графе H, т.е. если (v,w)Е, то (v,w)Е_1.

Таким образом, в подграфе, порожденном некоторым подмножеством вершин V₁, сохраняются все ребра исходного графа, инцидентные вершинам множества V₁.

Определение 8. Граф называется дополнением графа G=<V,E>, если .

Граф G называется самодополняемым, если он совпадает со своим дополнением (дополнительным графом), т.е. .

Множество вершин графа G и дополнительного графа совпадают, но две вершины являются смежными в дополнительном графе тогда и только тогда, когда они не являются смежными в самом графе G.

В терминах дополнения графа формулируется широко известная головоломка – задача Рамсея: доказать, что среди любых шести человек найдутся либо трое попарно знакомых, либо трое попарно незнакомых.

Действительно, указанную ситуацию можно описать графом G c шестью вершинами, представляющими людей; смежность двух вершин соответствует знакомству. При этом в дополнительном графе смежными будут те вершины, которые соответствуют незнакомым людям. Требуется доказать, что в G найдутся либо три попарно смежные, либо три попарно несмежные вершины. Наличие трех попарно смежных вершин в графе означает, что в нем в качестве подграфа есть треугольник. В этих терминах головоломку можно сформулировать так:

Теорема 2. Если G – граф с шестью вершинами, то либо G, либо содержит треугольник.

Доказательство. Пусть v – произвольная вершина графа G, имеющего шесть вершин. Так как вершина v смежна с любой из остальных пяти вершин или в G, или в , то, не теряя общности, можно считать, что вершины v₁, v₂, v₃ смежны с v в G. Если какие-либо две из вершин v₁, v₂, v₃ смежны в G, то вместе с v они образуют треугольник. Если никакие две из них не являются смежными в G, то вершины v₁, v₂, v₃ образуют треугольник в графе .

4.2. Способы задания графов. Изоморфизм графов.

Мы уже встречались с графическим заданием бинарных отношений, очевидно, что этот способ применим для графов. Изображение графа G=<V, E> получается путем расположения различных точек на плоскости для каждой вершины vV, причем, если (v,w)E, то точки, соответствующие вершинам v и w, соединяются линией (не обязательно прямой). При изображении орграфа направление ребра отмечается стрелкой, примыкающей к его концу. Графы не являются в полной мере «геометрическими» объектами, т.е. они выражают больше отношения между вершинами, чем расположение вершин и ребер в пространстве. Таким образом, граф, может быть изображен бесконечным количеством разных, но «эквивалентных» способов. Чтобы изображения графов не вводили в заблуждение, нужно помнить, например, что из пересечения двух ребер на рисунке не следует, что точка их пересечения является вершиной графа.

Если граф G можно изобразить на плоскости так, что его ребра не пересекаются, его называют планарным, а соответствующее изображение – картой.

Пример 1. Задать графически граф G = <V, E>, в котором множество вершин – V={v₁, v₂, v₃, v₄} и множество ребер – E={е₁=(v₁,v₂), е₂=(v₁,v₃), е₃ =(v₁, v₄), е₄=(v₂,v₃), е₅=(v₂,v₄), е₆=(v₃,v₄)}.

v ₁ . . v₂ v₁

. v₂

v₃ v₄ . v₃ v₄ .

а) б)

Рис. 7

Оба рисунка являются изображениями данного графа G, но на рисунке 7а) ребра е₂ и е₅ пересекаются, и точка их пересечения не является вершиной графа, а на рисунке 7б) нет. Таким образом, граф G является планарным, а рисунок 7б) – его картой.

Известно, что бинарное отношение может быть задано бинарной матрицей. Поскольку граф определяет и определяется отношением смежности вершин или отношением инцидентности вершин и ребер, то его можно задать с помощью матрицы смежности или с помощью матрицы инцидентности. Многие свойства графов определяются из их матричных представлений путем алгебраических преобразований. Рассмотрим более подробно эти способы задания.

Пусть задан (n,m)–граф G = <V, E>. Занумеруем его вершины V ={v₁, ..., v_n} и ребра E = {е₁, ..., е_m}. При этих обозначениях получаем следующие определения.

Определение 9 Матрицей смежности (n,m)–графа G называется квадратная бинарная матрица C=(c_{i j}) порядка n (i,j=1,2, ... n), в которой c_ij=1, если вершины v_i и v_j смежные ((v_i, _j)E), и c_ij=0 в противном случае ((v_i,v_j)Е).

Очевидно, что матрица смежности симметрична ( ) и ее главная диагональ состоит из нулей ( ).

Определение 10 Матрицей инцидентности (n,m)–графа G называется бинарная матрица порядка nm (i=1,2, ..., n; j =1,2, ..., m), в которой , если вершина v_i инцидентна ребру е_j, и в противном случае.

Если граф задан матрицей смежности или матрицей инцидентности, то степень вершины v_i равна сумме элементов i-ой строки матрицы.

Так как каждое ребро инцидентно только двум вершинам, то в каждом столбце матрицы инцидентности только два отличных от нуля элемента.

Для G ориентированного графа определение матрицы смежности переносится дословно. Ее отличие от матрицы смежности неориентированного графа состоит в том, что она в общем случае не будет симметричной. Определение матрицы инцидентности изменится следующим образом: , если вершина v_i является концом дуги e_j, , если вершина v_i является началом дуги e_j, и b_ij=0, если вершина v_i не инцидентна дуге e_j.

По матрице смежности графа (орграфа) всегда можно определить ребра графа (дуги орграфа) как пары инцидентных вершин. Однако, если ребра (дуги) были пронумерованы, то восстановить их номера по матрице смежности невозможно. В этом смысле матрица инцидентности является более информативной, поскольку позволяет получить полную информацию о ребрах (дугах), включая их нумерацию.

Матричный способ задания графов (орграфов) удобен для обработки их на ЭВМ. Однако следует отметить, что при большом количестве вершин матрица смежности оказывается громоздкой. То же замечание относится и к матрице инцидентности, размеры которой зависят еще и от количества ребер (дуг).

Пример 2. Составить матрицы смежности и инцидентности для графа G из примера 1.

Матрица смежности C(G) имеет порядок 4, а матрица инцидентности B(G) имеет размерность 45.

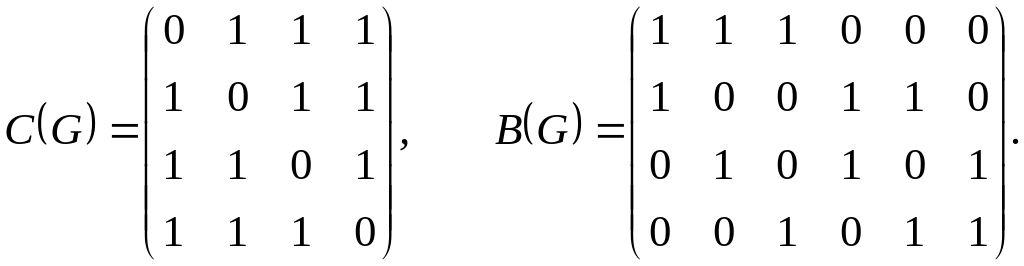
Очевидно, что вид матрицы смежности (инцидентности) зависит от выбранной нумерации вершин (и ребер). Имеет смысл не различать графы, которые различаются только нумерацией вершин, так как они фактически определяют одно и тоже отношение на множестве вершин. Введение новой нумерации множества V означает установления взаимно однозначного отображения множества V на себя. Эта идея лежит в основе понятия изоморфизма графов.

Определение 11 Два графа G=<V, E> и H=<X, Y> называются изоморфными (GH), если между множествами их вершин можно установить взаимно однозначное соответствие, которое сохраняет отношение смежности, т.е. существует взаимно однозначное соответствие : VX такое, что (v,w)E  ((v),(w))Y.

Понятие изоморфизма для орграфов определяется аналогично.

Непосредственно из определения 11 получаем следующие очевидные свойства изоморфных графов:

1) изоморфные графы имеют одинаковое число вершин (|V| = |X|);

2) изоморфные графы имеют одинаковое число ребер (|E| = |Y|);

3) любой вершине v степени (v) графа G в изоморфном графе H соответствует вершина (v) той же степени, т.е. в изоморфных графах равное число вершин одинаковой степени.

Невыполнение хотя бы одного из этих свойств указывает на то, что графы не являются изоморфными. Но даже если для графов G и H выполнены все три перечисленных выше условия, то это еще не гарантирует их изоморфизма. Задачи, связанные с решением вопроса об изоморфизме графов, достаточно сложны в общем случае. Инвариантом графа G называется такая его числовая характеристика, которая принимает одно и тоже значение для любого графа, изоморфного G. Число вершин и число ребер – это инварианты графа. Полный набор инвариантов определяет граф с точность до изоморфизма. Например, число вершин и число ребер образуют полный набор инвариантов для всех графов с числом вершин, меньшим четырех. В настоящее время для графов не известно ни одной полной нетривиальной системы инвариантов.

Пусть графы G и Н заданы матрицами смежности C(G) и C(H), соответственно. Если GH, что фактически означает перенумирацию вершин, то, переставляя строки и одновременно переставляя соответствующие столбцы матрицы C(G), мы должны получить матрицу C(H). Чтобы таким способом убедиться, что графы неизоморфны, придется выполнить все n! (n – число вершин графа) перестановок сток и столбцов, что является достаточно трудоемкой операцией.

Очевидно, что изоморфизм графов (орграфов) является отношением эквивалентности на множестве графов (орграфов). Задание абстрактного графа матрицей или графически фактически означает выбор некоторого представителя класса смежности.

4.3. Маршруты, цепи, циклы в графах. Связные графы.

Значительная часть теории графов и ее приложений занимается вопросами существования в графе так называемых маршрутов, т.е. последовательностей ребер, обладающих определенными свойствами.

Определение 12 Пусть G = <V, E > – граф. Маршрутом длины k в графе G из v в w (или (v,w)–маршрутом) называется последовательность <v₀, v₁, ..., v_k> вершин (необязательно различных) v_iV таких, что v₀=v, v_k=w, а (v_{i –1},v_i)E для всех i=1, 2, ..., k. Вершины v и w называются концевыми (v – начальной, w – конечной) вершинами маршрута, а остальные вершины – внутренними.

Ясно, что маршрут можно задать и последовательностью ребер: <e₁=(v₀,v₁), e₂=(v₁,v₂), ..., e_k=(v_k–1,v_k)>. Любой участок маршрута сам является маршрутом.

Маршрут называется цепью, если все его ребра различны и простой цепью, если все его вершины (возможно, кроме концевых вершин) различны.

Если в маршруте <v₀, v₁, ..., v_k> начальная и конечная вершины совпадают (v₀=v_k), то он называется замкнутым маршрутом. При этом обычно считают, что последовательности <v₀, v₁, ..., v_k>, <v₁, v₂, ..., v_k,v₀>, ..., <v_k, v₀, v₁, ..., v_k–1> – это различные записи одного и того же маршрута. Замкнутая цепь называется циклом, а замкнутая простая цепь простым циклом.

Пример 3. Для графа G, изображенного на рисунке 8, указать примеры различных видов маршрутов (цепь, простая цепь, цикл, простой цикл, маршрут, не являющийся цепью, замкнутый маршрут, но не цикл).

v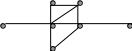 ₁ v₂

v₃ v₄ v₅ v₆

v₇

Рис.8.

Маршрут (v₃, v₄, v₁, v₂, v₄, v₇, v₅) является цепью, так как в нем нет повторяющихся ребер, но эта цепь непростая, поскольку вершина v₄ встречается дважды. Маршрут (v₃, v₄, v₇, v₅, v₂, v₁) дает примером простой цепи. Циклами, например, являются следующие маршруты (v₁, v₂, v₅, v₇, v₄, v₁) (v₁, v₂, v₄, v₅, v₁, v₄, v₁), причем, только первый из них – простой цикл. Очевидно, что маршрут (v₃, v₄, v₁ , v₂, v₄, v₁) нельзя назвать цепью, так как в нем повторяется ребро (v₄,v₁) = (v₁,v₄). Замкнутый маршрут (v₃, v₄, v₁ , v₂, v ₄, v₃) не является циклом, поскольку это не цепь.

Любая цепь является подграфом. Любой участок цепи или цикла – это цепь, а участок простой цепи или простого цикла – простая цепь.

Длина любого цикла в графе не меньше трех, так как по определению граф не содержит кратных ребер. Обхватом графа называется минимальная из длин всех его циклов.

Справедливы следующие достаточно очевидные утверждения:

1) для различных вершин v w любой (v,w)–маршрут содержит простую (v,w)–цепь;

2) всякий цикл содержит простой цикл;

3) объединение двух несовпадающих простых (v,w)–цепей содержит простой цикл.

С понятием маршрута тесно связано одно из важнейших понятий в теории графов – понятие связности.

Определение 13 Граф G называется связным, если любые две несовпадающие вершины (vw) соединены в нем (v,w)–маршрутом.

С помощью матрицы смежности графа можно решить как вопрос о числе (v,w)–маршрутов длины k в нем, так и вопрос о существовании (v,w)–маршрута.

Теорема 3. Пусть – матрица смежности графа , и . Тогда каждый элемент матрицы равен числу маршрутов длины k из вершины v_i в вершину v_j .

Следствие. Маршрут из вершины v_i в вершину v_j в графе существует тогда и только тогда, когда соответствующий элемент матрицы не равен нулю.

Пример 4. Для графа , где , найти а) число маршрутов длины 2 из v₃ в v₂; б) число маршрутов длины 3 из v₁; в v₂; в) убедится, что граф является связным.

Матрица смежности графа G имеет вид: 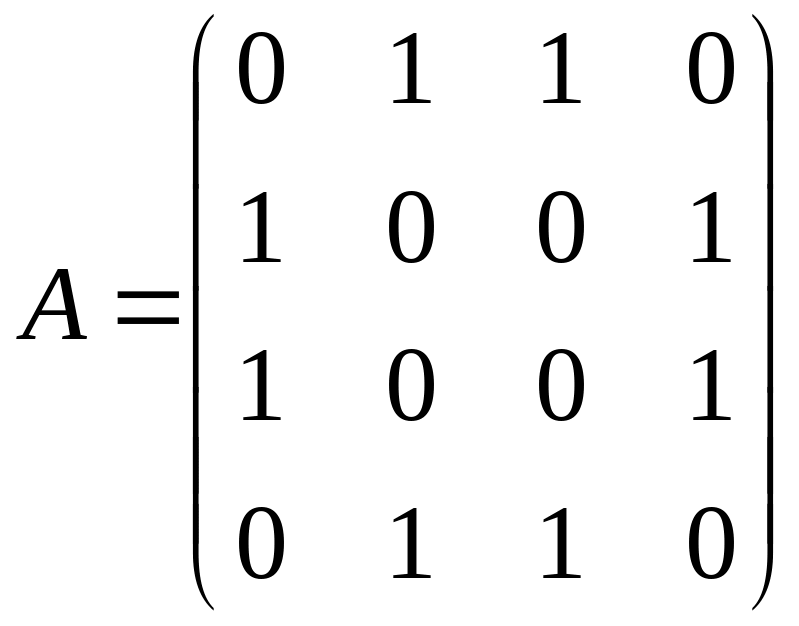. Найдем вторую и третью степени матрицы A.

, .

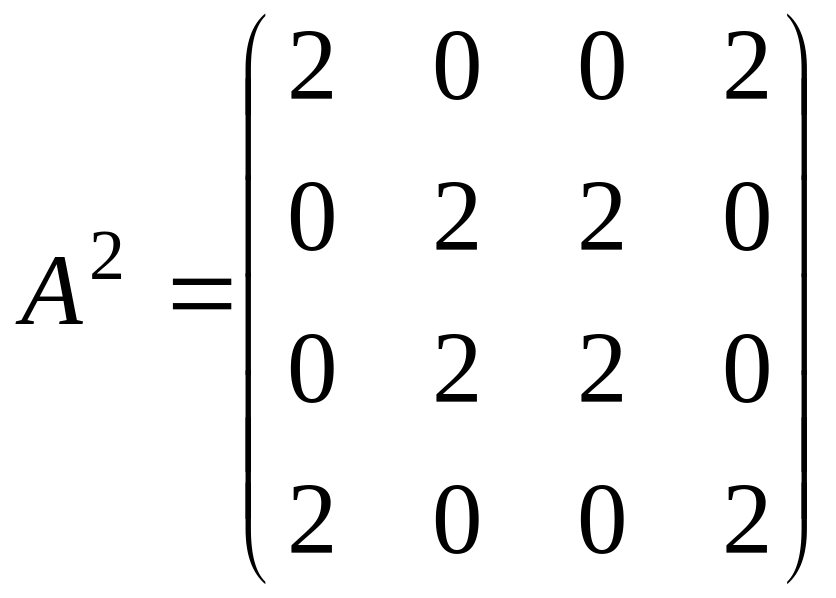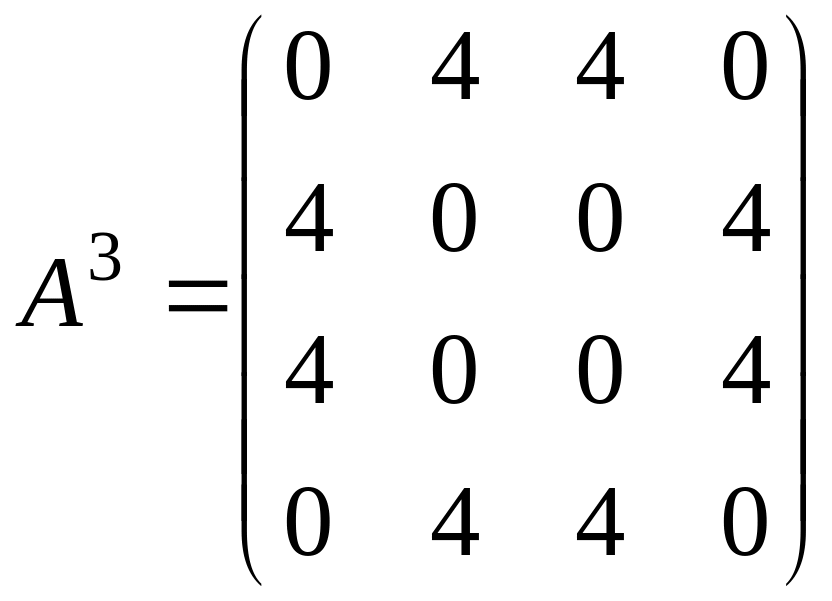На основании теоремы 4 по матрице определяем, что число маршрутов длины 2 из v₃ в v₂ равно двум. Аналогично, по матрице находим, что число маршрутов длины 3 из v₁ в v₂ равно четырем. Чтобы убедиться, что граф связный, найдем матрицу 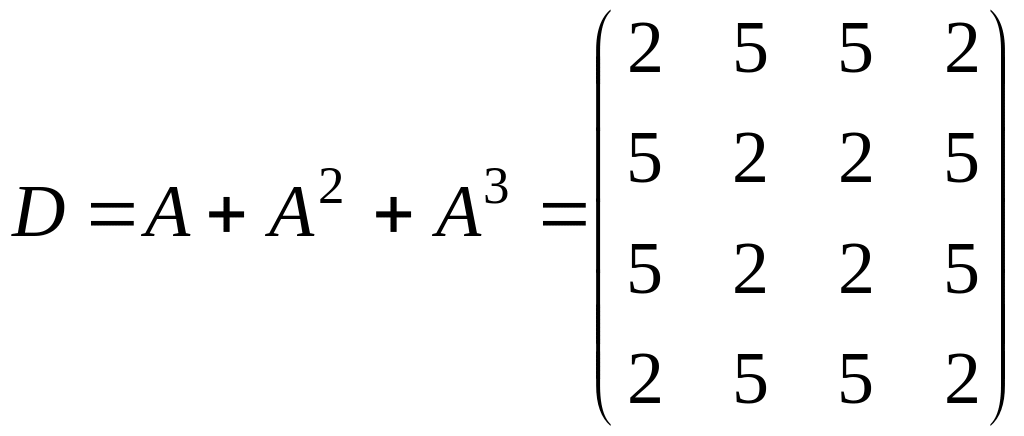. Все элементы матрицы D, соответствующие несовпадающим вершинам, отличны от нуля, что согласно следствию означает существование маршрутов между двумя любыми различными вершинами. Таким образом, по определению 13 граф является связным.

Следующая теорема выражает необходимое и достаточное условие связности графа.

Теорема 4. Для того чтобы граф G был связным, необходимо и достаточно, чтобы в нем для некоторой фиксированной вершины v и для любой другой вершины w существовал (v,w)–маршрут.

В силу утверждения 1) условие существования (v,w)–маршрута в определении 13 и в теореме 3 можно заменить условием существования (v,w)–цепи и даже простой цепи. Достаточно очевидно следующее утверждение:

для любого графа G либо сам граф G, либо его дополнение является связным графом.

На множестве всех вершин графа G = <V, E> введем отношение связности R* следующим образом: (v,w)R*  v=w или в G существует (v,w)–маршрут. Очевидно, что отношение R* рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности на множестве V вершин графа. Как всякое отношение эквивалентности R* задает разбиение множества V, т.е. V=V₁ V₂ … V_k, V_i V_j =  при ij. Множества V_i называются областями связности, а подграфы G_i = <V_i, E_i > (i=1,2, ..., k), порожденные областями связности V_i называются компонентами связности графа G. Каждая компонента связности представляет собой максимальный связный подграф графа G. Таким образом, мы получили следующее утверждение.

Теорема 5. Любой граф G является объединением своих компонент связности, т.е.

G = G₁G₂ ...G_k.

Ясно, что изоморфные графы имеют равное число k компонент связности. Сформулируем теоремы, в которых приведены некоторые полезные свойства связных графов и соотношения между основными числовыми инвариантами графа.

Теорема 6. Пусть G = <V, E> – связный граф и е – некоторое ребро графа G (eE). Тогда:

1) если ребро е принадлежит какому-либо циклу в G, то G\e – связный подграф

2) если ребро е не входит ни в какой цикл, то граф G\e имеет ровно две компоненты связности.

Отметим, что в теореме 6 через G\e обозначен подграф, полученный из графа G удалением ребра е с сохранением инцидентных ему вершин. Операция удаления вершины v из графа G заключается в удалении не только вершины v, но и всех инцидентных ей ребер.

Точкой сочленения графа называется вершина, удаление которой увеличивает число компонент связности графа; ребро с таким же свойством называется мостом. Если связный граф имеет точку сочленения (мост), то его можно превратить в несвязный, удалив точку сочленения (мост). Таким образом, если v – точка сочленения графа G, то граф G\v не является связным. Выделение точек сочленения помогает в изучении структуры связного графа.

Теорема 7. Если G = <V, E>– (n,m)-граф (|V|=n, |E=m) имеет k компонент связности, то справедлива следующая оценка:

В частности, для связного графа (k=1) имеем:

4.4. Обходы графов

Задача о кенигсбергских мостах, которую мы уже упоминали во введении, не только знаменует начало разработки теории графов, но и определяет одно из направлений этой теории, важных для приложений. Оно связано с задачами отыскания способов обхода (специальных маршрутов) графа.

Сформулируем задачу о кенигсбергских мостах. В городе Кенигсберге было два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рис. 9. Нужно было найти маршрут прохождения всех частей суши, который начинался бы с любой из них, кончался бы в этой же части и ровно один раз проходил по каждому мосту.

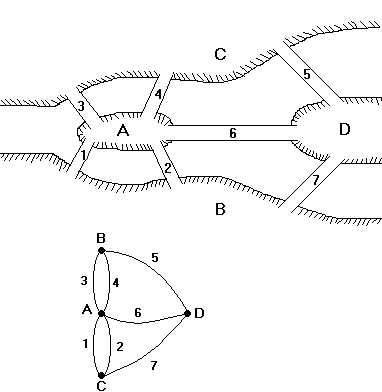
Рис. 9.

В 1736 году Эйлер доказал невозможность такого маршрута. Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился «граф» (точнее, согласно нашим определениям, «мультиграф»), изображенный на рис. 9. При этом обходу мостов соответствует последовательность ребер графа, в которой два ребра имеют общую вершину, т.е. маршрут. Так как в конце обхода нужно вернуться в исходную часть города и на каждом мосту нужно побывать только один раз, этот маршрут является простым циклом, содержащим все ребра графа.

Задачу об обходе мостов Эйлер обобщил и получил следующую проблему теории графов: можно ли в данном графе G найти простой цикл, содержащий все вершины и все ребра графа? В дальнейшем такие циклы получили название эйлеровых циклов, а графы, обладающие указанными циклами, – эйлеровым графами. Таким образом, эйлеров граф можно изобразить одним росчерком пера, не отрываясь от бумаги, причем процесс вычерчивания начинается и кончается в одной и той же точке. Ясно, что эйлеров граф должен быть связным. Эйлер нашел критерий существования в графе эйлерова цикла.

Теорема 8. Конечный граф является эйлеровым тогда и только тогда, когда он связен и степени всех его вершин четны.

Доказательство этой теоремы можно найти, например, в [1], причем эта теорема справедлива и для псевдографов (см. [2]).

В мультиграфе задачи о кенигсбергских мостах (см. рис. 9) все вершины имеют нечетную степень. Следовательно, она не имеет решения.

Кроме эйлеровых циклов рассматривают эйлеровы цепи, т.е. такие цепи, которые содержат все ребра конечного графа, но имеют различные начало v и конец w.

Теорема 9. Для того чтобы связный граф (псевдограф) обладал эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно две вершины нечетной степени.

Алгоритм выделения эйперовой цепи или эйлерова цикла в псевдографе, реализуемый на ЭВМ, можно найти в [2].

В теории графов широко известна так называемая задача коммивояжера:

коммерсант должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, и при этом стоимость такой поездки должна быть минимальной.

В терминах теории графов она формулируется следующим образом: в нагруженном графе определить цикл минимальной длины, проходящий через каждую вершину ровно один раз (под нагруженным графом понимается граф, в котором каждому ребру приписывается некоторое действительное число – «длина» ребра, а длина маршрута считается равной сумме длин составляющих его ребер). Прикладной характер этой задачи очевиден.

С задачей коммивояжера тесно связаны понятия гамильтонова цикла и гамильтонова графа. Гамильтоновым циклом в графе G называется такой цикл, который проходит через каждую вершину графа точно один раз. Граф G называется гамильтоновым графом, если в нем имеется гамильтонов цикл. Кроме того, можно определить и гамильтонову цепь. Понятие гамильтоновости переносится и на псевдографы.

Гамильтоновы циклы, как и эйлеровы, относятся к специальным маршрутам в графах. На первый взгляд эти понятия сходны. Но среди эйлеровых графов существуют как гамильтоновы, так и негамильтоновы графы, а среди гамильтоновых – эйлеровы и неэйлеровы графы (см. рис. 10). Таким образом, эти понятия независимы.

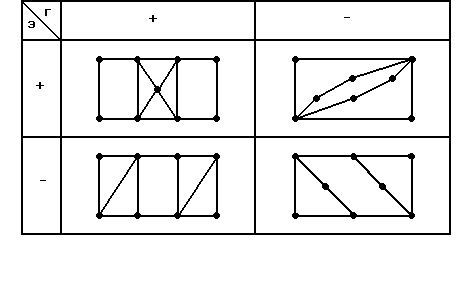
Рис.10.

Заметим, что (как и в случае эйлеровых графов) было бы полезно иметь сравнительно простые необходимые и достаточные условия существования гамильтоновых цепей и циклов. Однако этот вопрос является весьма сложным. Приведем некоторые сведения о гамильтоновых графах.

Очевидно, что граф, в котором каждая вершина смежна со всеми остальными вершинами (он называется полным графом) обладает гамильтоновыми циклами и цепями. Условие полноты графа можно рассматривать как простейшее достаточное условие того, что граф является гамильтоновым. Заметим, что в полном (n,m)-графе G каждая вершина v имеет наибольшую степень (v)=n–1, а число ребер максимально при заданном числе вершин: m=n(n–1). Более тонкие взаимосвязи между степенями вершин графа и свойством гамильтоновости содержатся в следующих достаточных условиях.

Теорема 10. Если в (n,m)- графе G n  3 и степени вершин удовлетворяют неравенству (v)+(w) n для любой пары v и w несмежных вершин, то G – гамильтонов граф.

Теорема 11. Если в (n,m)-графе G n  3 и степень любой вершины v удовлетворяет неравенству (v) , то G – гамильтонов граф.

Очевидным необходимым условием существования гамильтоновых цепей и циклов в графе G является его связность. А более тонкое необходимое условие гамильтоновости графа содержится в следующей теореме.

Теорема 12. Если граф G обладает гамильтоновым циклом, то в нем отсутствуют точки сочленения.

Простым способом выделения гамильтоновых цепей в графе является метод перебора всевозможных перестановок множества вершин V={v₁,v₂,…,v_n} графа G. Проверяем, является ли каждая такая перестановки маршрутом в G. Если да, то это означает, что найдена гамильтонова цепь, в противном случае переходим к следующей перестановке. После окончания перебора будут выделены все гамильтоновы цепи в графе G. Аналогично, для выделения всех гамильтоновых циклов перебираем все возможные перестановки вида v₁, v _i1, ... , v _in-1 множества вершин V, для каждой из которых проверяем, является ли последовательность вершин <v₁, v _i1, ... , v _{i n-1}, v₁>маршрутом в G. Очевидно, что при выделении всех гамильтоновых цепей придется перебирать n! перестановок, а при выделении всех гамильтоновых циклов – (n–1)! перестановок.

Описанный выше метод не учитывает информации об исследуемом графе G. Рассмотрим метод, аналогичный предыдущему, но использующий информацию о графе G. Составим всевозможные последовательности вершин , где , … , .

Через G(v) обозначено множество всех вершин графа G=<V, Е>, инцидентных вершине v, т.е. G(v)={w| wV и (v,w)Е}. Тогда в каждом случае, когда r=n, последовательность есть гамильтонова цепь в графе G. Соответственно, когда r=n и , последовательность является гамильтоновым циклом в графе G. Число переборов при использовании второго метода в общем случае меньше, чем для первого.

4.5. Деревья

Класс деревьев занимает особое положение в теории графов. Это связано с тем, что деревья во-первых, достаточно просто устроены (среди связных графов с фиксированным числом вершин дерево имеет наименьшее число ребер), а во-вторых, часто используются в прикладных задачах.

Определение 14 Деревом называется связный граф, не содержащий циклов.

На рисунке 11 изображены все (с точность до изоморфизма) деревья с шестью вершинами.

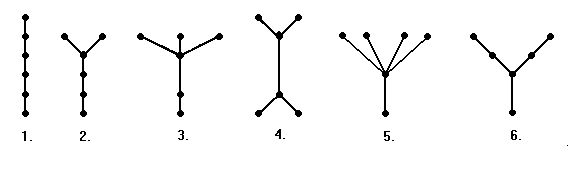
Рис.11.

Определение 15 Произвольный граф без циклов называется лесом (ациклическим графом).

Таким образом, любая компонента связности леса является деревом.

Существуют другие эквивалентные определения дерева, что отражено в следующей теореме.

Теорема 13. Для (n,m)-графа G следующие утверждения эквивалентны:

(1) G – дерево;

(2) G – связный граф и m=n–1;

(3) G – ациклический граф (лес) и m=n–1;

(4) в графе G любые две различные вершины соединены единственной простой цепью;

(5) G – ациклический граф со свойством: если пару его несмежных вершин соединить ребром, то G будет содержать ровно один цикл.

В качестве следствия получаем следующее утверждение:

в любом дереве с числом вершин n 2 имеется не менее двух концевых вершин (и хотя бы одно концевое ребро).

Действительно, если V={v₁, ..., v_n} – множество вершин дерева G и d₁, ..., d_n – степени соответствующих вершин, то d₁+...+d_n=2m=2(n–1). Но поскольку слагаемых n и каждое из них положительно, то, по крайней мере, два из них равны 1. Это означает наличие самое малое двух вершин степени 1, т.е. концевых. Справедливость утверждения для ребер следует из того, что концевым называется ребро, инцидентное концевой вершине, а при n=2 паре концевых вершин соответствует одно концевое ребро.

Определение 16 Остовным деревом связного графа G называется любой его подграф H, который содержит все вершины графа G и является деревом.

Если G – связный (n,m)-граф, то остовное дерево (если оно существует) должно содержать n–1 ребро (cм. теорему 13). Таким образом, любое остовное дерево связного графа G есть результат удаления из множества всех ребер ровно m–(n–1)=m–n+1 ребер. Число m–n+1 называется цикломатическим числом связного графа G и обозначается .

Существование остовного дерева в любом связном графе доказывает алгоритм выделения остовного дерева, который можно найти в [2]. Остовное дерево связного графа может быть выделено, вообще говоря, не единственным способом. Общее число остовных деревьев связного графа может оказаться весьма большим. Например, для полного графа с n вершинами оно равно n^n–2.

Понятие цикломатического числа для произвольного графа обобщают следующим образом. Пусть Н – остовной подграф графа G. Если он на любой области связности графа G порождает дерево, то Н называется остовом или каркасом графа G. Существование каркаса в любом графе G достаточно очевидно. Разрушая в каждой компоненте связности графа G циклы, т.е. удаляя «лишние» ребра, приходим к остову (каркасу). Число (G) ребер произвольного графа G, которое необходимо удалить для получения остова, не зависит от последовательности их удаления и определяется равенством (G)=m–n+k, где n – число вершин, m – число ребер, k – число компонент связности графа G. Число (G) называется цикломатическим числом графа G. Очевидны следующие утверждения:

(1) (G)=0  G – лес;

(2) (G)=1  G имеет только один цикл;

(3) граф G, в котором число ребер m не меньше числа вершин n (mn), содержит цикл.

СПИСОК ЛИТЕРАТУРЫ

1. ГавриловГ. П., Сапоженко А.А. Сборник задач по дискретной математике. – М: Наука, 1977.

2. Горбатов В.А. Основы дискретной математики: Учеб. Пособие для студентов вузов. – М.: Высш. шк., 1986.

3. Кук Д., Бейз Г. Компьютерная математика: Пер. с англ. – М.: Наука, 1990.

4. Кузнецов О. П., Адельсон–Вельский Г. М. Дискретная математика для инженера – М.: Энергоатомиздат, 1988.

5. Лавров И. А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории автоматов. – М.: Наука. 1984.

6. Лихтеренко Л. М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник–практикум и решения – СПб.: Изд–во «Лань»,1998.

7. Логинов Б. М. Лекции и упражнения по курсу «Введение в дискретную математику» – Калуга,1998.

8. Нефедов В.Н. Осипова В. А. Курс дискретной математики: Учеб.пособие. – М.: Изд–во МАИ, 1992.

9. Харари Ф. Теория графов. Пер. с англ. – М.: «Мир», 1973.

10. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979.

СОДЕРЖАНИЕ