
- •Моделирование случайных векторов и процессов
- •Метод Неймана.
- •Моделирование случайных векторов в корреляционной теории
- •1.Метод линейного преобразования
- •2.Метод канонических преобразований
- •3.Метод разложения в ряд Фурье
- •Моделирование типовых случайных процессов
- •Моделирование марковских случайных процессов
- •Моделирование случайных потоков
- •Моделирование случайных полей
- •Метод канонических разложений
- •Метод разложения в ряд Фурье
1.Метод линейного преобразования
Пусть задан N-мерный
вектор
![]() --
матрица-столбец с элементами
--
матрица-столбец с элементами
![]() .
Требуется получить N-мерный
вектор
.
Требуется получить N-мерный
вектор
![]() с
наперед заданной корреляционной матрицей
с
наперед заданной корреляционной матрицей
 , где M{}—математическое
ожидание
, где M{}—математическое
ожидание
и средними
![]() .
.
Диагональные члены
![]() --
дисперсии, а остальные – ковариации
координат вектора.
--
дисперсии, а остальные – ковариации
координат вектора.
Известно, что
производное линейное преобразование
А N-мерного
вектора
![]() сводится к умножению его на некоторую
матрицуN-мерного
порядка
сводится к умножению его на некоторую
матрицуN-мерного
порядка
![]() .
Матрица преобразования А выбирается
верхнетреугольной
.
Матрица преобразования А выбирается
верхнетреугольной![]() .
Элементы
.
Элементы![]() матрицы
матрицы![]() найдем из условий (*) :
найдем из условий (*) :![]() .
Таким образом
.
Таким образом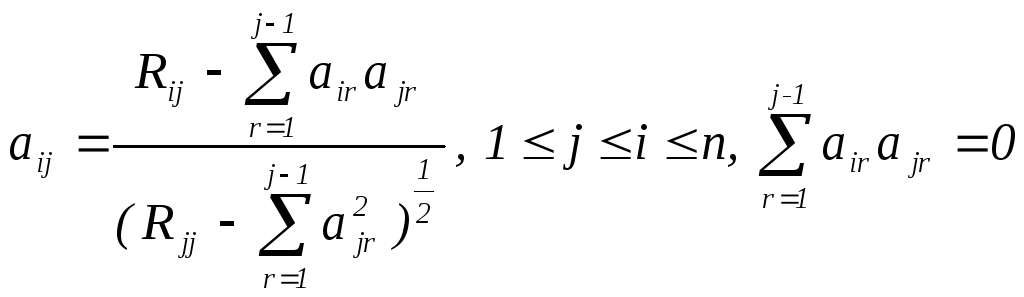 .
Рассмотренный процесс моделирования
позволяет получить лишь необходимые
корреляционные связи между координатами
случайного вектора. Закон распределения
может быть любым. Требуется только.
чтобы случайные координаты
.
Рассмотренный процесс моделирования
позволяет получить лишь необходимые
корреляционные связи между координатами
случайного вектора. Закон распределения
может быть любым. Требуется только.
чтобы случайные координаты![]() удовлетворяли условию (*).
удовлетворяли условию (*).
При больших N метод труднореализуем, так как для заполнения элементов матриц требуется большой объем оперативной памяти N(N+1)/2.
2.Метод канонических преобразований
Непрерывный
центрированный случайный процесс ξ(t)
может быть задан каноническим разложением
![]() ,
где
,
где![]() --
некоррелированные случайные коэффициенты
с параметрами
--
некоррелированные случайные коэффициенты
с параметрами![]() ;
;![]() -система
некоторых детерминированных координатных
функций. На практике бесконечный ряд
заменяется конечным. В качестве
координатных функций часто выбирают
ортонормированные координатные функции.
-система
некоторых детерминированных координатных
функций. На практике бесконечный ряд
заменяется конечным. В качестве
координатных функций часто выбирают
ортонормированные координатные функции.
3.Метод разложения в ряд Фурье
![]()
Недостатки методов 1,2,3 большой объем вычислений и большой объем памяти.
![]() и
и![]() --
случайные амплитуды.
--
случайные амплитуды.
Моделирование типовых случайных процессов
Рассмотренные выше методы моделирования случайных векторов и процессов в рамках многомерных распределений и корреляционной теории используются при моделировании. Однако в случае больших N требуется большое количество вычислений и большая подготовительная работа, что затрудняет их практическое использование. Чаще требуется моделировать процессы, относящиеся к узкому классу случайных воздействий. Для них могут быть построеныдостаточно эффективные моделирующие алгоритмы.
Для стационарных
нормальных случайных процессовнайдены
весьма экономичные моделирующие
алгоритмы. В основу их положено линейное
преобразование стационарной
последовательности x[n]
независимых случайных нормальных чисел
(дискретный белый шум) в последовательность
![]() , коррелированную по заданному закону.
При этом оператор линейного преобразования
записывается либо в виде скользящего
суммирования с некоторым весом
, коррелированную по заданному закону.
При этом оператор линейного преобразования
записывается либо в виде скользящего
суммирования с некоторым весом![]() либо как реккурентноеуравнение вида
либо как реккурентноеуравнение вида![]() в реккурентном уравнении существует
переходный процесс. Параметры
в реккурентном уравнении существует
переходный процесс. Параметры![]() и дискретная весовая функция
и дискретная весовая функция![]() определяются
на этапе подготовки к моделированию.
Задачу цифрового моделирования случайных
процессов с помощью скользящего
суммирования и реккурентных разностных
уравнений можно рассматривать как
задачу синтеза линейного дискретного
формирующего фильтра, который преобразует
дискретный белый шум в коррелированный
дискретный случайный процесс с заданными
корреляционно-спектральными
характеристиками. Сравнительная
характеристика методов моделирования
стационарных случайных процессов.
определяются
на этапе подготовки к моделированию.
Задачу цифрового моделирования случайных
процессов с помощью скользящего
суммирования и реккурентных разностных
уравнений можно рассматривать как
задачу синтеза линейного дискретного
формирующего фильтра, который преобразует
дискретный белый шум в коррелированный
дискретный случайный процесс с заданными
корреляционно-спектральными
характеристиками. Сравнительная
характеристика методов моделирования
стационарных случайных процессов.
Моделирование марковских случайных процессов
Важное теоретическое
и практическое значение имеют марковские
случайные процессы. С точки зрения
моделирования на ЭВМ марковские
случайные процессы – один из наиболее
простых процессов. Действительно,
марковским называется случайный процесс
![]() ,
у которого условная плотность распределения
вероятностей:
,
у которого условная плотность распределения
вероятностей:![]() значений
значений![]() в произвольный момент времени
в произвольный момент времени![]() удовлетворяет соотношению
удовлетворяет соотношению![]() т.е. зависит лишь от значений процесса
в один из предшествующих моментов
времени.W-
плотность вероятностей перехода из
состояния
т.е. зависит лишь от значений процесса
в один из предшествующих моментов
времени.W-
плотность вероятностей перехода из
состояния
![]() в
в![]() ,
,![]() ,
,![]() --
это функция четырех переменных.
--
это функция четырех переменных.
Для моделирования
марковского случайного процесса
достаточно знать условную плотность
вероятностей перехода
![]() и плотности вероятностей
и плотности вероятностей![]() значения
значения![]() в
в![]() .
.
Алгоритм получения дискретных значений процесса сводится к следующему:
1)Формируется
реализация
![]() случайной
величины
случайной
величины![]() с
с![]() .
.
2)Генерируется
реализация
![]() случайной
величины
случайной
величины![]() с
с![]() и т.д.
и т.д.
Таким образом
получаем последовательность чисел
![]() изображающую дискретную реализацию
изображающую дискретную реализацию![]() марковского случайного процесса
марковского случайного процесса![]() с
заданной условной плотностью вероятностей
перехода
с
заданной условной плотностью вероятностей
перехода![]() .
Для получения следующей реализации
процесса повторяется та же операция.
.
Для получения следующей реализации
процесса повторяется та же операция.
В более общем
случае рассматриваются N-мерные
марковские процессы, т.е. N
взаимосвязанных между собой процессов
![]() .
В этом случае условная плотность
вероятности имеет вид
.
В этом случае условная плотность
вероятности имеет вид![]() .
.
Тогла моделирование N-мерных марковских процессов по заданной условной плотности вероятностей перехода в принципе не отличается от моделирования рассмотренных выше одномерных марковских процессов. Однако, поскольку на каждом шаге требуется реализация N-мерных случайных векторов, то моделирование марковских процессов является сложной задачей.
