
- •10 Инт. Вида ,
- •11 Инт. Вида
- •3 Извлечение корня из кч
- •1 Кч в алгебраической форме
- •2 Тригонометрическая форма кч
- •3 Извлечение корня из кч
- •4 Основная теорема алгебры и ее следствия
- •7 Инт. Рациональных функций.
- •7 Инт. Рациональных функций.
- •8.2 Инт. Биномиальных дифференциалов
- •4. Формула Ньютона/Лейбница.
7 Инт. Рациональных функций.
Рациональной
фун. или дробью наз. отношение двух
полиномов, R=P/Q,
где
![]() .
.
Дробь
R
наз. правильной если
![]() ,
и она наз. неправильной если
,
и она наз. неправильной если
![]() .
.
Простейшими наз.правильные дроби вида
![]() .
.
Всякую правильную дробь можно представить суммой простейших дробей, и такое представление ед.
Правило составления суммы: знаменатель разл. на неприводимые множители; каждый множитель порождает столько простейших каков показатель с которым он входит в разложение;
Если дробь R неправильная, то ее можно представить в виде
суммы
![]() ,
где
,
где
![]()
целая часть(полином), а
целая часть(полином), а
![]()
правильная дробь.
правильная дробь.
![]() ,
где
,
где
![]()
простейшие дроби.
простейшие дроби.
Инт.
от дроби находим по формуле
![]()
8 Инт. иррациональных функций
8.1 Инт. дробно-линейных иррац.
8.2 Инт. Биномиальных дифференциалов
1) p целое, 2) (m+1)/n целое, 3) (m+1)/n+p целое.
**8.3 Инт. кв. иррац., подстановки Эйлера
![]()
![]() ,
,
![]() =
=![]()
9 Инт. тригон. выражений
9.1 , ;
9.2 , , , ;
9.3 , , , ;
9.4
пр.
![]() ,
,
![]()
Опред. интегралы
1. Опред.
2. Свойства ( лин., адд., монот.)
3. Т. о ср.знач.
4. Формула Ньютона/Лейбница.
5. Т. о дифф. по верхнему пределу
6. Замена переменной
7. Инт. по частям опред. интегралов.
1.
Опр.
Пусть f
опред. и ограничена на отрезке
![]() ,
,
![]()
разбиение
,
разбиение
,![]() ,
,
![]()
ранг
разбиения,
ранг
разбиения,
![]() инт.
сумма f,
инт.
сумма f,
![]() предел
инт. сумм,
предел
инт. сумм,
определенным
интегралом от f
по
наз. число
![]() ,
,
если предел , при этом f наз. инт. по Риману.
Пример
![]()
Справедлива следующая
Т. Если f опред. и ограничена на отрезке , и имеет там конечное число точек разрыва, то она инт. на .
2. Свойства
1)
Лин.
![]()
2)
Адд.
![]()
3)
Монот. (1)
![]() ;
(2)
;
(2)
![]()
3.
Т. о ср.знач. f
непр. на
![]() :
:![]() ,
,
![]() наз.
ср. знач. f
на
.
наз.
ср. знач. f
на
.
док.
![]()
4.
Формула Ньютона/Лейбница Если
f
инт. на
, и
дифф. функция F
на
: F'=f
, тогда
![]() .
.
док.
![]()
5. Т. о дифф. по верхнему пределу
Если
f
непр. на
, а
![]() , тогда
, тогда
![]()
док.
![]()
6. Замена переменной
Пусть
f
непр. на
,
непр. дифф. и
на
![]() ,
,
![]()
![]() ,
,
если
на
,
![]()
![]()
док. использовать формулу Н/Л
7. Инт. по частям опред. интегралов.
Несобственные инт.
1 Опр. несоб. инт. 1-го рода(с бесконечными пределами) , сх и рсх.
Пр.
![]()
2 Признаки сх. и рсх.
2.1)
Принцип Коши:
![]() сх
сх
![]()
2.2)Пусть
![]() первообразная
первообразная
![]() ,
сх
существует
,
сх
существует
![]()
Пр.
![]()
2.3)
Признак сравнения: если
![]() и
и
![]() сх., то
сх.
сх., то
сх.
2.4)
Предельный признак сравнения: если![]() и
и
![]() ,
то инт.
и
оба сх. или оба
рсх.
,
то инт.
и
оба сх. или оба
рсх.
2.5)Если
![]() сх., то сх. инт.
;
инт.
наз. абс сх.,
сх., то сх. инт.
;
инт.
наз. абс сх.,
обратное не верно!
3 Опр. несоб. инт. 2-го рода(от неограниченных функций), сх и рсх.
4 Признаки сх. и рсх. такие же как для инт. 1-го рода.
Приложения инт.
1 Пл. крив. трапеции и сектора. Пусть f непр. и ≥ 0 на , тогда ее подграфик E наз. крив. трапецией.
Т.
Крив. трапеция измерима, и ее пл.
![]()
Пусть
f
непр. , ≥ 0 на
![]() и E
соответствующий крив. сектор, тогда его
пл.
и E
соответствующий крив. сектор, тогда его
пл.
![]()
пр.
1) пл. эллипса, 2) пл. 1-ой арки циклоиды
![]() ,
,
![]() ,
,
![]() ,
пл. фигуры ограниченной кардиоидой.
,
пл. фигуры ограниченной кардиоидой.
2 Объем тел вращения, поперечные сечения
![]()
пр.
объем 1) тора, 2)
![]() вокруг
OX
и OY,
3) эллипсоида
вокруг
OX
и OY,
3) эллипсоида
3 Стат. моменты и центр масс крив. трапеции, формулы Гульдина
пр. центр масс полукруга
4 Длина гладкой кривой (гладкого пути)
![]() ,
,
![]() ,
,
![]()
5 Пл. поверхности вращения гл. кривой
![]()
6 Стат. моменты и центр масс гл. кривой, формулы Гульдина
стат.
моменты:![]() ,
,![]() ;
;
центр
масс:
![]() ,
,![]() ;
;
формулы
Гульдина:
![]() ,
,![]() .
.
Пр. ЦМ полуокружности.
DУ.
0 Задачи, которые приводят к DУ
1 Основ. понятия и определения.
DУ, порядок, DУ1, решение, ЗК, ОР, частное, общий интеграл, геометрическое толкование.
2 Некоторые типы DУ1, решение которых сводится к инт.
2.1 DУ с разделяющимися переменными
2.2 Однородные DУ1
2.3 Лин. DУ1, методы вариации и Бернулли
2.4 DУ Бернулли, сведение к лин. уравнению, метод Бернулли
2.5 DУ в полных дифференциалах, условие Эйлера, решение с помощью частных производных, решение инт. параллельно координатным прямым. Инт. множитель зависящий от x или от y
3 Существование и единственность решения ЗК для DУ1
1. Основные понятия и опр. Уравн., содержащее неизвестную фун. и ее производные наз. дифференциальным. Порядком DУ наз. наибольший порядок производной неизвестной фун., которая входит в уравнение.
Т.о.
DУ1
имеет вид
![]() ,
его записывают в виде
,
его записывают в виде
![]() ,
где
непр. в области
,
где
непр. в области
![]() ,
DУ2,
разрешенное относительно
,
DУ2,
разрешенное относительно
![]() , имеет вид
, имеет вид
![]() ,
где
непр. в области
,
где
непр. в области
![]() .
.
Фун.
![]() наз. реш. DУ
наз. реш. DУ
![]() в
в
![]() ,
если
,
если
1)![]() непр.,
непр.,
2)![]() ,
,
3)
![]() .
.
График реш. наз. инт. кривой, само реш. наз. интегралом DУ, особенно когда реш. имеет неявный вид.
Пр.
![]()
Реш.
![]() DУ
, график которого проходит через
DУ
, график которого проходит через
![]() :
:![]() ,
наз. реш. ЗК с началом
,
наз. реш. ЗК с началом
![]() .
ЗК записывают в виде
.
ЗК записывают в виде
![]() . Семейство реш.
. Семейство реш.
![]() наз. ОР в
если
наз. ОР в
если
![]() ,
т.о. за счет выбора
,
т.о. за счет выбора
![]() решается ЗК с началом в любой точке Ω.
решается ЗК с началом в любой точке Ω.
Пр.
y=(2(x−c)/3)3/2
дает ОР DУ
![]() в
области y>0.
в
области y>0.
Если в каждой точке ИК нарушается ед., то она наз. особой.
Пример: y=0 особое решение DУ y = y1/3
2. DУ1, решения которых сводится к интегралам
1
DУ
с РП,
![]() .
.
2
ОDУ1,
![]() .
.
Уравн.,
приводимые к однородным
![]() .
.
3
ЛDУ1
![]() ,
метод Бернулли, пр.
,
метод Бернулли, пр.
![]() .
.
4
DУ
Бернулли:
![]() ,
0 и 1, метод Бернулли.
,
0 и 1, метод Бернулли.
5
Уравн. в полных дифф. Пусть
,
уравн.
![]() наз.
в ПD
в
наз.
в ПD
в
![]() если левая часть является полным
дифференциалом некоторой фун. двух
переменных, т.е.
u
:
если левая часть является полным
дифференциалом некоторой фун. двух
переменных, т.е.
u
:![]() ,
тогда ОР имеет вид
,
тогда ОР имеет вид
![]() .
.
Пусть односвязная область в R2 , а M и N непр. дифф. в , тогда
![]() будет
полным дифференциалом т. и т.т. когда
выполнено условие Эйлера:
будет
полным дифференциалом т. и т.т. когда
выполнено условие Эйлера:![]() в
.
в
.
6 Уравн. с инт. множителем зависящим от x или от y.
3. Сущ. и ед. решения DУ1.
Рассмотрим (без док) 2 теоремы сущ. и ед. реш. ЗК для DУ в .
1
Т. Пусть 1)
непр. в
и 2)
![]() ограничена в
,
ограничена в
,
сущ. ед. реш. ЗК с началом в любой точке .
Пример: ЛDУ1 , p и q непр. на .
2 Т. Пусть
1) −прямоугольник : x − x0 a, y−y0 b,
2)
f
непр. в
и значит ограничена:![]() ,
,
ИК
, проходящая через
![]() и опред. в промежутке
x−x0
h,
h=min(a,
b/M
), если
кроме того 3)
ограничена в Ω, то ИК ед.
и опред. в промежутке
x−x0
h,
h=min(a,
b/M
), если
кроме того 3)
ограничена в Ω, то ИК ед.
Пр.
1)
![]() ;
2)
;
2)
![]()
*********************************************************************
пропустить
DУ1, неразрешенные относительно y (схемы решений)
1.
![]() .
Пусть α0
−корень уравнения
.
Пусть α0
−корень уравнения
![]() ,
тогда y
=0
,
,
тогда y
=0
,
y=0 x+c, 0 =(y c)/x, а F((y c)/x)=0 −общий интеграл, все!
2.
![]() . Пусть
. Пусть
![]() ,тогда
,тогда
![]() ,
найдем x:
,
найдем x:
![]() ,
,
![]() ,
,![]() ; получили общий интеграл в парам. форме:
; получили общий интеграл в парам. форме:
![]() ,
все!
,
все!
Пр.
![]() .
.
3.
![]() .
Пусть p=y
,тогда x=F(p),
dy=pdx=pF(p)dp,
y=
pF(p)dp=(p)+c;общий
интеграл: x=F(p),
y=
(p)+c,
все!
.
Пусть p=y
,тогда x=F(p),
dy=pdx=pF(p)dp,
y=
pF(p)dp=(p)+c;общий
интеграл: x=F(p),
y=
(p)+c,
все!
Пр.
![]() .
.
4.
![]() . Пусть
,
тогда
. Пусть
,
тогда
![]() ,
dy=Fx
dx+Fp
dp=pdx
,
,
dy=Fx
dx+Fp
dp=pdx
,
получили
уравнение для x:
![]() ,
его решение (x,
p,
c)=0
вместе с y=F(x,p)
дают решение исходного уравнения в
парам. форме, все!
,
его решение (x,
p,
c)=0
вместе с y=F(x,p)
дают решение исходного уравнения в
парам. форме, все!
5.
![]() . Пусть p=
y,
тогда
. Пусть p=
y,
тогда
![]() ,
,
![]() ,
,
получили уравнение для y: M(y,p)dy+N(y,p)dp=0, его решение (y,p,c)=0 вместе с x=F(y,p) дает решение исходного уравнения, все!
Пр. xy−y+(1+( y)2 )1/2 =0, y=xy +(1+( y)2 )1/2 , y=xp +(1+p2 )1/2 ,
p=p+xp +pp(1+p2 )1/2 , ( x +p(1+p2 )1/2 ) p =0.
*********************************************************************
DУ2.
1.
Определения. DУ2,
разрешенное относительно
![]() ,
имеет вид
,
имеет вид
![]() ,
где f
непр. в обл.
,
где f
непр. в обл.
![]() .
.
Реш.
уравн. наз. фун.
:
![]()
![]() ,
разумеется
,
разумеется
![]() .
.
ЗК
заключается в отыскании решения
![]() ,
где
,
где
![]() ,
при этом
должно быть опред. в некоторой окрест.
т. x0
. ЗК записывают в виде
,
при этом
должно быть опред. в некоторой окрест.
т. x0
. ЗК записывают в виде![]() .
Два последних равенства наз. условиями
Коши, т.
.
Два последних равенства наз. условиями
Коши, т.
![]() наз. начальной.
наз. начальной.
Пусть
через
![]() проходит ровно
одна ИК . ОР наз. семейство решений
проходит ровно
одна ИК . ОР наз. семейство решений
![]() ,
зависящее от двух параметров
,
зависящее от двух параметров
![]() ,
для которого система
,
для которого система
![]() разрешима относ.
разрешима относ.
![]() .
.
Т.о. за счет выбора решается ЗК с началом в любой точке Ω
2 Сущ. и ед. решения.
Т.
Пусть 1) f
непр. в Ω, 2)![]() огранич. в Ω
ЗК в Ω имеет ед. реш.
огранич. в Ω
ЗК в Ω имеет ед. реш.
Пр.1)![]() , 2)
, 2)
![]() ,
p,
q
непр. на
.
,
p,
q
непр. на
.
3 Понижение порядка. Имеются частные случаи DУ2, когда оно сводится к DУ1, такая процедура наз. понижением порядка.
1)
![]() ,
имеем
,
имеем
![]() ,
,
![]()
2)
![]() , пусть z=
y
, тогда z
= f(x,
z
), это DУ1,
решим его
, пусть z=
y
, тогда z
= f(x,
z
), это DУ1,
решим его
z
=
(x,
c1
), теперь y
=
(x,
c1
),
![]() . Пр.
. Пр.
![]()
3)
![]() ,
пусть z=
y
, тогда
,
пусть z=
y
, тогда
![]() ,это
DУ1,
решим его z
=
(y,
c1
), теперь y
=
(y,
c1
), это DУ
с РП, его решение:
,это
DУ1,
решим его z
=
(y,
c1
), теперь y
=
(y,
c1
), это DУ
с РП, его решение:
dy/ (y, c1 )=x + c2 плюс y= , где ( , c1 )=0.
Пр.
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
ЛDУ
1. Опред. Пусть n≥1, ЛDУ n−го порядка наз. уравнение вида
![]() ,
где функции
,
где функции
![]() непр. на [a,b].
Уравнение опред. в полосе, которая
занимает (a,b)
вдоль x
, а y,
y,
… y(n−1)
могут принимать любые значения.
непр. на [a,b].
Уравнение опред. в полосе, которая
занимает (a,b)
вдоль x
, а y,
y,
… y(n−1)
могут принимать любые значения.
Левую
часть обозначим через
![]() , так что ЛDУ
удобно записывать в виде
, так что ЛDУ
удобно записывать в виде
![]() . Уравн. наз. однородным если
. Уравн. наз. однородным если
![]() и неоднородным если
и неоднородным если
![]() .
.
Пр.
1)
![]() −ЛНDУ1,
можно решить по формуле ОР,
−ЛНDУ1,
можно решить по формуле ОР,
2)
![]() −ЛОDУ2,
можно понизить порядок,
−ЛОDУ2,
можно понизить порядок,
3)
![]() −это
знаменитое уравнение Эри, решение
которого можно представить с помощью
степенного ряда.
−это
знаменитое уравнение Эри, решение
которого можно представить с помощью
степенного ряда.
Вид
ЛDУ
обеспечивает однозначную разрешимость
ЗК всюду в полосе. Для ЛDУ2
![]() это означает, что для любого набора
это означает, что для любого набора
x0 (a,b), y0 , z0 R сущ. ед. решение y : y( x0 )= y0 , y( x0 )= z0 .
Более того, для ЛDУ теорема сущ. утверждает, что решение ЗК опред.
во всем интервале (a,b).
Введем
понятие лин. завис. и незав. фун. Конечный
набор функций
![]() наз. лин. завис., если сущ. числа 1,
2,
…m
, не все =0, такие, что
наз. лин. завис., если сущ. числа 1,
2,
…m
, не все =0, такие, что
![]() ,
если сумма =0 лишь когда все i
=0, то
набор наз. лин. незав.
,
если сумма =0 лишь когда все i
=0, то
набор наз. лин. незав.
Т.
Набор функций лин. зависим
одна из функций равна лин. комбинация
других:
![]() ,
при некотором j.
,
при некотором j.
Пр.
1)
![]() − лин. незав.
− лин. незав.
2)
![]() − лин. завис.
− лин. завис.
3)
![]() − лин. незав.
− лин. незав.
![]() определитель
Вронского набора функций.
определитель
Вронского набора функций.
Т.
Набор
лин. зависим
![]()
док: один из столбцов W = лин. комбинации других,
2. ЛОDУ (структура общего решения)
Рассмотрим
однородное уравнения
![]() .
.
1.
Множ. всех решений ЛОDУ
образует лин. пространство: их можно
складывать и умножать на числа как
векторы. Это следует из линейности
выражения
:
![]()
2.
Если
![]() лин. незав. решения ЛОDУn,
то W(x)
0 x
лин. незав. решения ЛОDУn,
то W(x)
0 x
док:
допустим что
x0
:
![]() , тогда столбцы в
, тогда столбцы в
![]() лин. зав.,
лин. зав.,
![]() , рассмотрим решение
, рассмотрим решение
![]() ,
,
по
теореме ед.
![]() ,
что противоречит лин. незав., все!
,
что противоречит лин. незав., все!
3.
Пусть
![]() решения уравнения
, набор
решения уравнения
, набор
лин.
независимый
![]() .
.
4. Опред. ФСР ЛОDУn наз. лин. незав. набор из n его решений.
Пример
− ФСР уравнения
![]() .
.
5. Для ЛОDУ n−го порядка сущ. ФСР .
док:
n=2,
берем x0
, y1
– решение ЗК с началом в т.
![]() , а y2
– решение ЗК с началом в т.
, а y2
– решение ЗК с началом в т.
![]() ,
набор y1
, y2
– ФСР, т.к.
,
набор y1
, y2
– ФСР, т.к.
![]() .
.
6.
ОР ЛОДУn
имеет вид
![]() ,
где
,
где
![]() − ФСР.
− ФСР.
док: всякая такая комбинация является решением, это следует из лин., любое решение ЗК реализуется в таком виде, это следует из того, что W(x) 0 x , все!
3. ЛОDУ2 с постоянными коэфф.
Рассмотрим
уравн.
![]() ,
где p,
q
− действ. числа. Будем искать решение
в виде y=exp(x)
, подстановка дает кв. уравн. 2+p+q=0
, оно наз. характ. Пусть d=p2/4−q
дискриминант
,
где p,
q
− действ. числа. Будем искать решение
в виде y=exp(x)
, подстановка дает кв. уравн. 2+p+q=0
, оно наз. характ. Пусть d=p2/4−q
дискриминант
1)
![]() −два действ.
различных корня,
−два действ.
различных корня,
y1=exp(1x) и y2=exp(2x) образуют ФСР (доказать)
ОР y=c1 exp(1x)+c2 exp(2x) ;
2) d=0: 1=2=−p/2 −действ. корень крат. 2 , y1=exp(1x), покажем, что y2=xexp(1x) тоже решение:
L2(xex )=L2(dex /d)=dL2(ex )/d=d((2 +p+q)ex )/d=
(2 +p)ex +x(2 +p+q)ex =0 при =1 , y1 , y2 образуют ФСР (доказать)
ОР y=(c1 +c2 x)exp(1x) ;
3) d<0: 1,2=−p/2 ±i(−d)1/2 = ± iβ −пара сопряженных корней, составляем комплексные решения z1,2=e(x± iβ)x=ex(cosβx±isinβx);
действ. решения y1 =ex cosβx , y2 =ex sinβx образуют ФСР (доказать)
ОР y= ex(c1 cosβx+c2 sinβx).
4. ЛНDУ
Рассмотрим
неоднородное уравнения
![]() .
.
1.
Теорема. ОР ЛНDУ
имеет вид
![]() , где z
–ЧР ЛНDУ,
а
, где z
–ЧР ЛНDУ,
а
![]() − ОР ЛОDУ
− ОР ЛОDУ
![]() .
.
2. Отыскание ЧР ЛНDУ2 с пост. коэфф. и с прав. частью спец. вида
y +a y+b y = f(x), a, b R1 ;
2.1)
![]()
![]() ,
где r
крат.
,
где r
крат.
![]() как корня характ. уравн.,
как корня характ. уравн.,
пр. y − y =x , y − y=x .
2.2)![]()
![]() ,
где r
крат.
,
где r
крат.
![]() как корня характ. уравн
как корня характ. уравн
пр. y +4y=cosx , y + y=sinx .
2.3)
![]()
![]() ,
Uk
, Vk
полиномы степ. k=max(m,
n).
,
Uk
, Vk
полиномы степ. k=max(m,
n).
2.4) Суперпозиция решений f = f1 + f2 , z1 –ЧР ЛНDУ f1 , а z2 f2
z= z1 + z2 f
3 Метод Лагранжа
Рассмотрим
ЛНDУ2
![]() .
.
ОР ЛОDУ2 y=c1y1+ c2y2 , где y1 ,y2 − ФСР.
Ищем решение НУ в виде
z=c1 (x)y1+ c2 (x)y2 , где c1(x), c2(x) подлежат определению,
дифференцируем z=c1 y1+c2 y2 + c1 y1 + c2 y2
полагаем c1 y1+c2 y2 =0, тогда z= c1 y1+c2 y2
дифференцируем еще раз z= c1 y1+c2 y2+c1 y1+c2 y2,
потребуем чтобы L2(z)= f(x):
c1 y1+c2 y2+c1 y1+c2 y2+p(x)(c1 y1+c2 y2 )+ q(x)(c1 y1+ c2 y2 )= f(x),
c1 y1+c2 y2 = f(x)
получили лин. систему c1 y1+c2 y2 =0, c1 y1+c2 y2 = f(x)
ее опред. W≠0, находим производные c1 и c2 ,
и после интегрирования функции c1 и c2 , а значит и z, все!
пр.
![]() .
.
СDУ. 1. Основные понятия и опред.
1. Нормальной СDУ наз. набор уравн. вида
![]()
![]()
...
![]()
где fi i1..n непр. в области Rn+1 .
Каждое уравнение НС 1−го порядка, разрешенное относ. производной. На самом деле уравнение вида y(n)=f(x, y, y,…y(n1)) можно переделать в НСDУ.
Пр. y= f(x, y, y ): t=x, x1=y, x2=y x1=x2 , x2= f(t, x1 ,x2 ).
2. Решением СDУ наз. набор фун. 1,2,…n , опред. на интервале
( , β) : k(t)=fk (t, 1 (t), 2 (t),… n (t)) t( , β) k1..n
3.
Удобно записывать НСDУ
в векторной форме:
![]() , где
, где
![]() ,
,
![]() ,
,
![]() , решение СDУ
будет векторная функция
= (1,…n
): (t)=f
(t,
(t))
t(
, β)
, решение СDУ
будет векторная функция
= (1,…n
): (t)=f
(t,
(t))
t(
, β)
4.
ЗК для СDУ
записывается в виде
![]() ,
,
![]() ,
т.
,
т.
![]() наз. начальной. ОР наз. семейство решений
наз. начальной. ОР наз. семейство решений
![]() , зависящее от n
констант, за счет выбора которых можно
решить ЗК с началом в любой т. из Ω.
, зависящее от n
констант, за счет выбора которых можно
решить ЗК с началом в любой т. из Ω.
2 Сущ. и ед. решения НСDУ
Пусть
1) все фун.![]() непр. в Ω , 2) все ЧП
непр. в Ω , 2) все ЧП
![]() ограничены
в Ω ,
ограничены
в Ω ,
тогда сущ. ед. решение ЗК с началом в любой т. из Ω.
3 Метод исключения
Для определенности рассмотрим систему из 2-х уравнений
![]() ,
,
![]()
Берем
1-е уравн.
![]() и дифф. его
и дифф. его
![]() .
.
В результате получаем систему
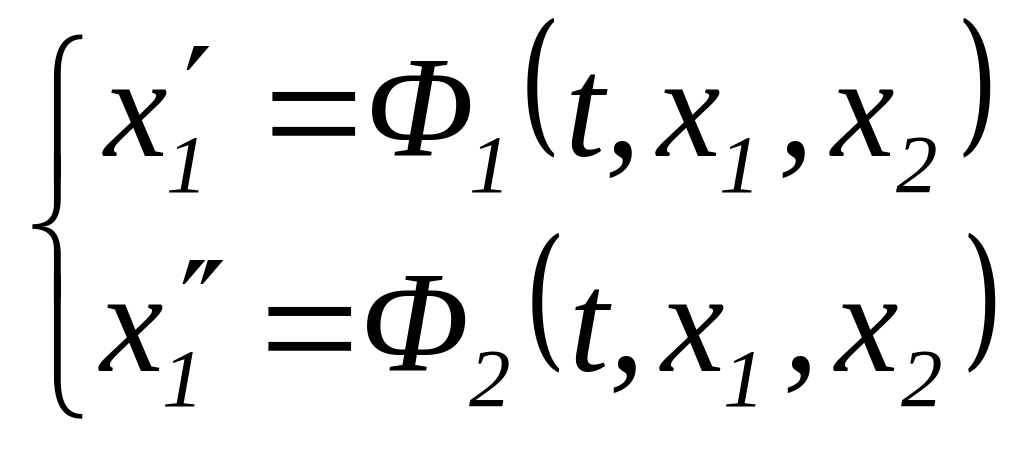
исключаем x2 и получаем DУ2 относительно x1 .
Пр.
![]()
окончание 2-го семестра
****************************************************************************
ФМП
Невырожденные поверх. 2-го порядка
эллипсоид 1)
![]()
гиперболоиды 2)
![]() 3)
3)
![]()
конус 4)
![]()
параболоиды 5)
![]() 6)
6)
![]()
цилиндры 7)
![]() 8)
8)
![]() 9)
9)
![]()
Опр.
фмп. Обозначим
через
![]() множ.
всех упорядоченных пар действительных
чисел; так что
элемент из
имеет
вид
множ.
всех упорядоченных пар действительных
чисел; так что
элемент из
имеет
вид
![]() ,
,
![]() .
.
Пусть
![]() ,
фун. двух переменных наз. правило
,
которое
,
фун. двух переменных наз. правило
,
которое
![]()
ставит
в соответствие опред. число
![]() ,
при этом
,
при этом
![]() наз. обл. опр.
.
наз. обл. опр.
.
Пр.
![]() ;
;
![]() ;
;
![]()
Подобным образом опр. фун. трех переменных
Пр.
![]() ;
;
![]() ;
;
![]()
Предел
и непр. Открытым
кругом в
с центром в т.
![]() и радиуса r
наз. множ.
и радиуса r
наз. множ.
![]() всех
всех
![]() для которых
для которых
![]() ,
такой круг наз. окр. т.
.
,
такой круг наз. окр. т.
.
Пусть
,
![]() наз. предельной т.
если
ее окр. содержит т. из
отличную от
.
наз. предельной т.
если
ее окр. содержит т. из
отличную от
.
Число
наз. пределом
в т.
:
![]() если
>0
если
>0
![]() :
:
![]() как только
как только
![]() и
и
![]() .
.
Пр.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Фун.
f
наз. непр. в т.
если она опр. в т.
и
![]()
Частные производные и дифференциал
1
ЧП. Пусть
фун. 2-х переменных, частной производной
(1-го порядка) f
в т.![]() по x
наз. число
по x
наз. число
![]() если предел
, ЧП обозначают так
если предел
, ЧП обозначают так
![]() ,
если
,
если
![]() ,
сходным образом вводится ЧП
,
сходным образом вводится ЧП
![]() .
.
ЧП выч. по обычным правилам и формулам дифф., надо лишь учитывать что при выч. ЧП по x величина y=const, и наоборот x=const когда берется ЧП по y.
2
Дифференциал. Пусть
,
она
наз. дифф. в т.
если ее приращение
![]() ,
,
гл.
часть![]() лин.
относительно
лин.
относительно
![]() и
и
![]() наз. дифференциалом и обозначается
наз. дифференциалом и обозначается
![]() .
Пр.
.
Пр.
![]() (вычислить!)
(вычислить!)
Теорема 1(необх. условие дифф.)
дифф.
в т.
непр.
в т.
и
![]() ,
,![]() .
.
![]()
Пр.
![]()
Теорема 2(дост. условие дифф.)
![]() и
и
![]() непр. в т.
дифф. в т.
непр. в т.
дифф. в т.
Свойства d
![]()
Приложение d
основано
на соотношении
![]() :
:
![]()
Пр.![]()
3 Дифференцирование сложных функций
(A) Пусть 1) дифф. в т.
2)
![]() дифф. в т. t0
дифф. в т. t0
3)
![]()
4)
![]()
h
дифф. в т. t0
и
![]()
(B) Пусть 1) дифф. в т.
2)
![]() дифф.
в т.
дифф.
в т.
![]()
3)
![]()
4)
![]()
h
дифф. в т.
![]() и
и
![]() ,
,
![]()
Инвариантность формы дифференциала.
Пр.
4 Повторное дифференцирование.
Опред. ЧП 2-го порядка наз. ЧП от ЧП 1-го порядка.
Пр.
![]() ,
оператор Лапласа u=0.
,
оператор Лапласа u=0.
Пусть
![]() , тогда можно образовать 4 ЧП 2го
порядка:
, тогда можно образовать 4 ЧП 2го
порядка:![]()
Теорема
![]() там, где они непрерывные
там, где они непрерывные
док.
берем
![]()
=![]() ,
дважды применяем
формулу Лагранжа и переходим к пределу
,
дважды применяем
формулу Лагранжа и переходим к пределу
![]() .
.
если ЧП 2го порядка фун. n переменных непр., то их всего n(n+1)/2
Опред.
Пусть
,
![]() =
=![]()
5 Производная по направлению и градиент
Пусть
![]() и
и
![]() ненулевой
вектор(направление),
ненулевой
вектор(направление),
производной
в
т.
![]() в направлении
наз. число
в направлении
наз. число
![]() , если
предел .
, если
предел .
Можно
считать что
![]()
орт. Положим
орт. Положим
![]() ,
а
,
а
![]()
![]() )
производная в нуле справа.
)
производная в нуле справа.
По теореме о производной сложной функции, получим
![]() скалярное
произведение.
скалярное
произведение.
Вектор
![]() наз. градиентом
в
т.
наз. градиентом
в
т.![]() ,
,
![]() проекция
градиента на
.
проекция
градиента на
.
Если
орт градиента, то
![]() .
.
Т.о.
![]() дает направление наибольшего возрастания
,
дает направление наибольшего возрастания
,
а его длина = скорости возрастания.
6 Касательная плоскость
Опр. Пусть задана в окрестности U т. , S ее график,
![]() и
и
![]() ,
,
![]() ,
плоскость
, проходящая через
наз. касат. к S
в т.
если
,
плоскость
, проходящая через
наз. касат. к S
в т.
если
![]() при
условии, что
при
условии, что
![]() .
.
Теорема
о касат. плоскости. S
имеет касат. плоскость в т.
дифф. в т.
,
при этом уравн.
имеет вид:
![]()
вектор
![]() ,
и смотрит вверх,
,
и смотрит вверх,
а
уравн. нормали
![]()
Пр.
![]() .
.
Экстр. фун. двух переменных
Опр.
Пусть
![]() опред. в открытом множ.
R2
,
наз. т. мин., если
из некоторой окр. т.
выполняется неравенство
опред. в открытом множ.
R2
,
наз. т. мин., если
из некоторой окр. т.
выполняется неравенство
![]() ,
при этом
,
при этом
![]() наз. мин. значением, если неравенство
является строгим, то
наз. т. строгого мин. Подобным образом
опред. т. макс. и макс. значение. Экстремум
объединяет мин. и макс.
наз. мин. значением, если неравенство
является строгим, то
наз. т. строгого мин. Подобным образом
опред. т. макс. и макс. значение. Экстремум
объединяет мин. и макс.
Теорема.
Если
т. экстремума
и
![]() и
и
![]() ,
,
то
![]()
Опр.
![]() наз. стац. т.
если
.
наз. стац. т.
если
.
Т.о.
если
![]() т. гл. экстремума, то
стац. т., обратное неверно.
т. гл. экстремума, то
стац. т., обратное неверно.
Пр.
![]() ,
(0, 0)
стац. т. но в ней нет экстремума .
,
(0, 0)
стац. т. но в ней нет экстремума .
Дост. условия экстр.(n=2)
Пусть
![]() 2 раза непр. дифф. в окр. стац. т.
2 раза непр. дифф. в окр. стац. т.
![]() ,
,
положим
![]() ,
,
1)
если
![]() ,
то
т. экстр., мин. при
,
то
т. экстр., мин. при
![]() и макс.
и макс.
при
![]() ;
;
2)
если
![]() ,
то в т.
нет экстр.
,
то в т.
нет экстр.
3)
если
![]() ,
то необх. дополнительное исследование
,
то необх. дополнительное исследование
Квадратичные формы
Кв.
формой в Rn
наз. выраж. вида
![]() ,
,
![]()
матрица
кв. формы q,
матрица
кв. формы q,
q
наз. положительно опред. если
![]() ,
,
q
наз. отрицательно опред. если
![]()
q наз. знакопеременной если она принимает значения как >0 так и <0.
Пр.
Обозначим
через
![]() диагональные миноры матрицы A
диагональные миноры матрицы A
Критерий Сильвестра определенности кв. формы:
(С1)
q
положительно опред.
все
![]()
(С2)
q
отрицательно опред.
![]() и т.д.
и т.д.
Достаточные условия экстремума(n≥2)
Пусть
фун.
![]() 2 раза непр. дифф. в окр. стац. т.
2 раза непр. дифф. в окр. стац. т.
![]() ,
,
и
q
кв. форма с коэфф.
![]() ,
,
(Э1)
если q
положительно опред., то
![]() т. min
т. min
(Э2) если q отрицательно опред., то т. max
(Э3) если q знакопеременная, то в т. нет экстр.
Пр.
![]()
Неявные функции
1
НФ 1-й переменной. Пусть
![]() опред. в окр. V
т. x0
, она наз. неявно заданной уравнением
опред. в окр. V
т. x0
, она наз. неявно заданной уравнением
![]() если
если
![]() .
.
Здесь
![]() фун. двух переменных, задана в круге U
с центром в т.
фун. двух переменных, задана в круге U
с центром в т.
![]() , где
, где
![]() .
Пр.
.
Пр.
![]() .
.
Теорема.
Пусть 1)
![]() ,
,![]() непр.
в U,
2)
непр.
в U,
2)
![]() , 3)
, 3)
![]() ,
,
тогда
непр. дифф. НФ
и
![]()
2 НФ 2-х переменных
Опр.
Пусть
![]() определена в окрест. V
т.
,
она наз. неявно заданной уравнением
определена в окрест. V
т.
,
она наз. неявно заданной уравнением
![]() если
если
![]() .
Здесь
.
Здесь
![]() фун. трех переменных , задана в шаре U
с центром в т.
фун. трех переменных , задана в шаре U
с центром в т.
![]() ,
где
,
где
![]() .
Пр.
.
Пр.
![]() .
.
Теорема. Пусть (n≥2)
1) y , xi непр. в U(X0 , y0) при всех i ,
2) y (X0 , y0) 0,
3) (X0 , y0)= 0,
тогда непр. дифф. НФ y=f(X) и fxi(X)= xi /y
Приложение: касат. плоскость к поверхности заданной неявно.
![]() ,
,
![]() ,
,
![]()
x(M0 )(x x0 )+ y(M0 )(y y0 )+ z(M0 ) (z z0 )=0 касательная плоскость к S в т. M0 ,
(x x0 )/ x(M0 )= (y y0 )/ y(M0 )= (z z0 )/ z(M0 ) уравнение нормали.
DУ
1 Задачи, которые приводят к DУ
2 Основ. понятия и опред.
DУ, порядок, DУ1, решение, ЗК, ОР, частное, общий интеграл,
геометрическое толкование.
3 Некоторые типы DУ1, решение которых сводится к инт.
DУ с разделяющимися переменными
Однородные DУ1
Лин. DУ1, методы вариации и Бернулли
DУ Бернулли, сведение к лин. уравнению, метод Бернулли
DУ в полных дифференциалах, условие Эйлера,
решение с помощью частных производных,
решение инт. параллельно координатным прямым
Инт. множитель зависящий от x или от y
4 Сущ. и ед. решения ЗК для DУ1
5 DУ2
Основ. понятия. Вид, решение, ЗК, ОР, сущ. и ед. решения ЗК
Понижение порядка
ЛDУ. Основ. понятия и опред.
вид , однородные и неоднородные уравн.,
пр.
1)
,
2)
,
3)
![]()
сущ. и ед. решения ЗК (определено во всем интервале (a,b))
лин. завис. и незав. теорема о лин. завис.
Пр. 1) , 2) , 3)
опред. Вронского W(x)
Т. Набор лин. зависим
ЛОDУ
1. Множ. решений ЛОDУ образует лин. пространство
2. Если лин. незав. решения ЛОDУn, то W(x) 0 x
3. Пусть решения уравн. ,
набор лин. незав. W(x) 0 x.
4. Опред. ФСР ЛОDУn , пример −ФСР уравн. .
5. Для ЛОDУn сущ. ФСР .
6. ОР ЛОДУn имеет вид , где − ФСР.
ЛОDУ2 с пост. коэфф.
ЛНDУ
ОР, нахождение частного решения ЛНDУ2 с пост. коэфф.
Метод Лагранжа
СDУ
1 Основ понятия и опред. норм. форма, ЗК и ОР
2 Сущ. и ед. решения ЗК
3 Метод исключения
