Второй семестр.

Вопросы

1 КЧ в алгебраической форме, модуль и сопряжение

2 Тригонометрическая форма КЧ, формула Муавра

3 Извлечение корня из КЧ

4 Первообразная и неопределенный инт., определения и свойства

5 Теорема о подстановке и замена переменной в неопределенном инт.

6 Инт. по частям неопределенных инт., рекуррентная формула для

7 Инт. рациональных функций

8 Инт. биномиальных дифференциалов

9 Инт. вида

10 Инт. Вида ,

11 Инт. Вида

12 Определение и свойства определенного инт.,

13 Теорема о среднем значении

14 Формула Ньютона/Лейбница

15 Теорема о дифф. по верхнему пределу

16 Замена переменной в определенном интеграле

17 Площади и объемы, ст. моменты и ЦМ криволинейной трапеции, формулы Гульдина;

18 Длина и пл. поверхности вращения, ст. моменты и ЦМ гл. кривой, формулы Гульдина;

19 Несоб. инт. 1-го и 2-го рода, признаки сх. и рсх.

20 ДУ с разделяющимися переменными

21 Однородные ДУ 1-го порядка

22 Линейные ДУ 1-го порядка

23 ДУ Бернулли

24 ДУ в полных дифференциалах

25 ДУ допускающие интегрирующий множитель зависящий от x или от y

26 Понижение порядка

27 Линейная завис. и независ. функций, определитель Вронского

28 ФСР и общее решение ЛОДУ2

29 ЛОДУ2 с пост. коэф., d>0

30 ЛОДУ2 с пост. коэф., d=0

31 ЛОДУ2 с пост. коэф., d<0

32 Общее решение ЛНДУ2

33 ЛНДУ2 с пост. коэф. и с правой частью спец. вида

34 Метод Лагранжа для ЛНДУ

Комплексные числа

1 Кч в алгебраической форме

Опр. КЧ наз. упорядоченная пара действительных чисел, множ. всех КЧ обозначается через C. Так что означает, что , где .

Два КЧ наз. равными, , если и .

Сумма и произведение определяются по формулам

КЧ вида отождествим с действительными числами : .

Обозначим , тогда ,

получим алгебраическую форму КЧ: ,

, .

Сумма и произведение в алгебраической форме имеет вид

, ,

надо как обычно раскрывать скобки, приводить подобные и помнить что .

Деление КЧ. Пусть , тогда , при этом z наз. частным, обозначается в виде дроби и выч. формуле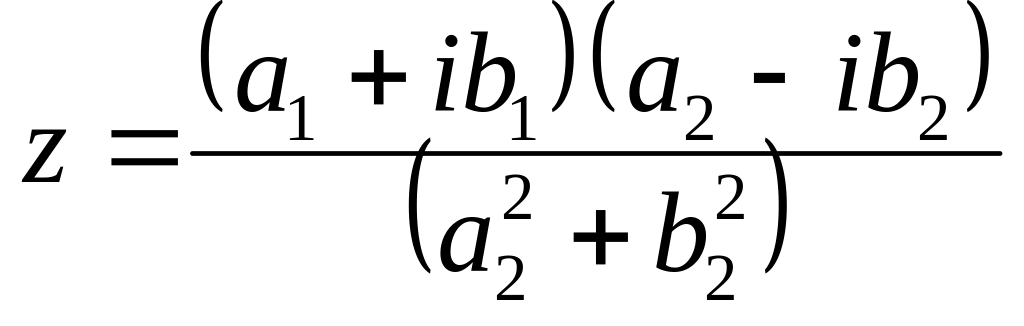

Модуль и сопряжение. Пусть , модулем z наз число , сопряженным к z наз. число

2 Тригонометрическая форма кч

, ,

Равенство в ТФ :  и

Умножение и деление в ТФ

 ,

Формула Муавра

Показательная форма КЧ

положим , тогда всякое КЧ

можно записать в показательной форме

3 Извлечение корня из кч

Пусть и , число наз. корнем n-ой степени из z если ,

при этом пишут .

Теорема. Пусть и , тогда  ровно n корней n-ой степени из z, т.е. решений уравнения , которые даются формулой

, .

Квадратные корни из КЧ можно найти по формуле

Примеры

4 Основная теорема алгебры и ее следствия

Теорема Гаусса. Всякий полином степени с комплексными коэфф. имеет хотя бы один корень в C.

Следствия

1) Всякий полином степени с комплексными коэфф. разлагается в целиком на лин. множители.

2) Всякий полином степени с действительными коэфф. разлагается в на неприводимые множители не выше второй степени.

Неопределенные инт.

1. Основные понятия и опред. Пусть опред. на , фун. заданная на наз. первообразной фун. если .

Справедлива следующая

Теорема. Если непр., то она имеет первообразную.

Неопределенным инт. от наз. множ. всех ее первообразных и обозначается символом . Вид всех первообразных можно усмотреть из след. предложений (доказываются дифференцированием)

(1) если первообразная , то тоже первообразная ;

(2) если и  первообразные , то

 , где одна из первообразных, а C=const.

Зам. Дифф. элем. фун. снова приводит к элем. фун., однако операция инт. может привести к не элем. фун. Пр. не элем. фун.