3. Другие характеристики вариационного ряда.

Кроме указанных выше, применяют и другие характеристики вариационного ряда. Укажем главные из них.

Модой называют варианту, которая имеет наибольшую частоту.

Медианой называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. , то 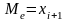; при четном 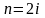медиана .

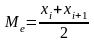Размахом варьирования 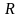называют разность между наибольшей и наименьшей вариантами: .

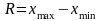Средним абсолютным отклонением называют среднее арифметическое абсолютных отклонений: .

Коэффициентом вариации называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней: %.

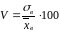Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов. Тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше. Коэффициент вариации – безразмерная величина, поэтому он пригоден для сравнения рассеяний вариационных рядов, варианты которых имеют различную размерность, например, если варианты одного ряда выражены в сантиметрах, а другого – в граммах.

Если вариационный ряд составлен по данным выборки, то все описанные характеристики называются выборочными, если по данным генеральной совокупности, то - генеральными.

4. Эмпирические моменты.

Для вычисления сводных характеристик выборок используют эмпирические моменты, аналогичные соответствующим теоретическим моментам. Обычным эмпирическим моментом порядка s называется среднее значение s-ых степеней разностей 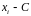, где – наблюдаемая варианта, С-произвольная постоянная (ложный ноль – либо мода, либо любая варианта, расположенная примерно в середине вариационного ряда):

.

При С=0 имеем начальные эмпирические моменты порядка s; в частности, в случае s=1

.

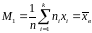Центральным эмпирические моменты порядка s называется обычный момент при :

.

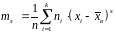В частности, центральный момент второго порядка

,

т.е. совпадает с выборочной дисперсией.

5. Асимметрия и эксцесс эмпирического распределения.

Нормальное распределение является одним из самых распространенных в применениях математической статистики. Для оценки отклонения эмпирического распределения от нормального используют следующие характеристики: асимметрию эмпирического распределения и эксцесс эмпирического распределения. Смысл этих характеристик аналогичен смыслу асимметрии и эксцесса теоретического распределения.

Асимметрия эмпирического распределения определяется следующим равенством .

Эксцесс эмпирического распределения определяется следующим равенством .

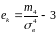В формулы входят центральные эмпирические моменты и , а также выборочное среднее квадратическое отклонение σ_в.

6. Число степеней свободы.

Статистические оценки параметров теоретического распределения являются случайными величинами, так как получаются они на основе случайной выборки. Для многих задач математической статистики (построение доверительных интервалов, проверка статистических гипотез и т.д.) оказывается необходимым рассмотрение законов распределения статистических оценок или их комбинаций. При этом широко используются такие законы распределения случайных величин, как хи-квадрат, Фишера, Стьюдента и некоторые другие.

В выражения указанных законов входят величины, называемые степенями свободы. Любая композиция независимых случайных величин , , …, , в частности сумма, имеет степеней свободы, так как каждая составляющая может менять свое значение независимо от других значений. Различные независимые измерения одной и той же величины можно рассматривать как различные случайные величины с числом степеней свободы, равным числу измерений. Так, например, последовательность измерений , , …, или их сумма имеет степеней свободы. Точно так же и сумма квадратов этих величин имеет степеней свободы.

Однако если для рассмотренной системы случайных величин задана некоторая связь, то количество степеней свободы уменьшается. В частности, если найти среднее значение полученных в результате выборки значений , , …, и зафиксировать это значение для соответствующих случайных величин , , …, , т.е. признать верным выражение 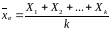для всех значений этих величин, то одну из величин всегда можно выразить через остальные. Это значит, что она оказалась связанной и система случайных величин потеряла одну степень свободы.

Таким образом, рассматривая случайную величину выборочной средней как сумму независимых случайных измерений, ее число степеней свободы следует принять равным числу этих измерений. Если же рассматривать выборочную дисперсию как случайную величину

, то она будет иметь уже на одну степень свободы меньше, так как здесь фиксировано и связывает случайные величины , , …, .

Если после фиксации выборочной средней и выборочной дисперсии ( , ) рассматривать случайную величину, зависящую от независимых случайных величин и от и , то ее число степеней свободы будет меньше еще на единицу.