Глава 14. Двойной интеграл

§14.1 Предварительные замечания.

Def: Кривая называется простой, если её можно разбить на конечное число частей так, чтобы каждая из частей была записана уравнением, либо , либо .

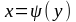Т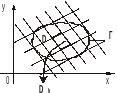 еорема: Если замкнутая область D на плоскости XOY ограничена простой кривой, то она имеет площадь.

Разобьём область D сетью простых линий на n – частей. Каждая часть Dk будет иметь площадь (т.к. по теореме она ограничена простой кривой).

Def: Диаметр области Dk – наибольшее расстояние между двумя точками, принадлежащими области Dk (обозначим dk).

§14.2 Задача, приводящая к понятию двойного интеграла.

Пусть функция - функция двух переменных, 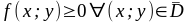, где 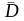- это некоторая замкнутая область D, ограниченная простой кривой Г.

Def: Тело, ограниченное плоскостью XOY, поверхностью и с боков цилиндрической поверхностью, образующая которой // оси OZ, а направляющей служит контур Г, ограничивающий область D, называется цилиндроидом.

Для вычисления объёма данного цилиндроида выполним следующие операции:

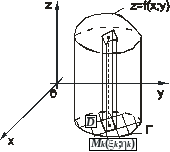
1. Обозначим площади областей Dk, 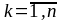через @ Диаметры областей Dk, через -@

2. Построим на простых кривых разбиения области d цилиндроиды, тогда

@ , где Vk – объём цилиндроида с основанием Dk.

3. Для нахождения Vk выберем в области Dk произвольную точку , тогда, @ т.к. верхняя граница цилиндроида – поверхность произвольной формы, заменена участком плоскости параллельным xOy

@

4.

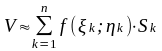
5. Это равенство тем точнее, чем больше площадок деления области d, и чем меньше диаметр этих площадок.

@

К отысканию предела подобных сумм для функций двух переменных приводят самые разнообразные задачи, а не только задача об объёме цилиндрического тела.

§14.3 Определение двойного интеграла.

Пусть в области D, ограниченной контуром Г, задана функция . Проделаем пять операций:

1. Разобьём область сетью простых кривых на n областей

@

Обозначим площади этих областей @ диаметры @ причём @

2. Выберем в каждой площадке точку 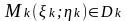, вычислим значения функции в выбранных точках 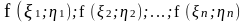и составим произведения: @

3. Просуммируем эти произведения: @

- интегральная сумма Римана.

4. П ри увеличении числа площадок деления, при условии, что 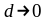, получаем предел интегральных сумм Римана. Если этот предел существует, конечен и не зависит от способа разбиения области D и выбора точек , то он определяет двойной интеграл функции по области D и обозначается: @

Замечание: Если двойной интеграл по области 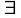, то функция называется интегрируемой в области D.

Теорема: Если функция непрерывна в области _, имеющей площадь, то она интегрируема в этой области.