
- •Класифікація і зведення до канонічного вигляду квазілінійних рівнянь з частинними похідними: випадок гіперболічного рівняння.
- •Класифікація і зведення до канонічного вигляду квазілінійних рівнянь з частинними похідними: випадок параболічного рівняння.
- •Класифікація і зведення до канонічного вигляду квазілінійних рівнянь з частинними похідними: випадок еліптичного рівняння.
- •4.Коливання струни: виведення хвильового рівняння.
- •5.Формула д’аламбера (розв’язування задачі Коші для хвильового рівняння)
- •6.Розв’язувння змінної задачі для напівнескінченної струни за допомогою формули д’аламбера
- •7. Коливання обмеженої струни (стоячі хвилі)
- •8. Вимушені коливання однорідної струни
- •9. Виведення рівняння теплопровідності
- •10. Розв’язування змішаної задачі дифузійного типу методом відокремлення змінних
- •11. Перетворення неоднорідних (гу) у дифузійних задачах в однорідні
- •12. Задача коші для рівняння теплопровідності
- •13. Граничні умови в задачах дифузійного типу
- •14. Хвильове рівняння і граничні умови
- •15.Еліптичні задачі. Три основні типи граничних умов у крайових задачах
- •15. Еліптичні задачі. Три основні типи граничних умов в крайових задачах.
5.Формула д’аламбера (розв’язування задачі Коші для хвильового рівняння)
Розглянемо задачу Коші для одновимірного хвильового рівняння
(ДРЧП)![]() ,
,![]() ,
,![]()
(ПУ)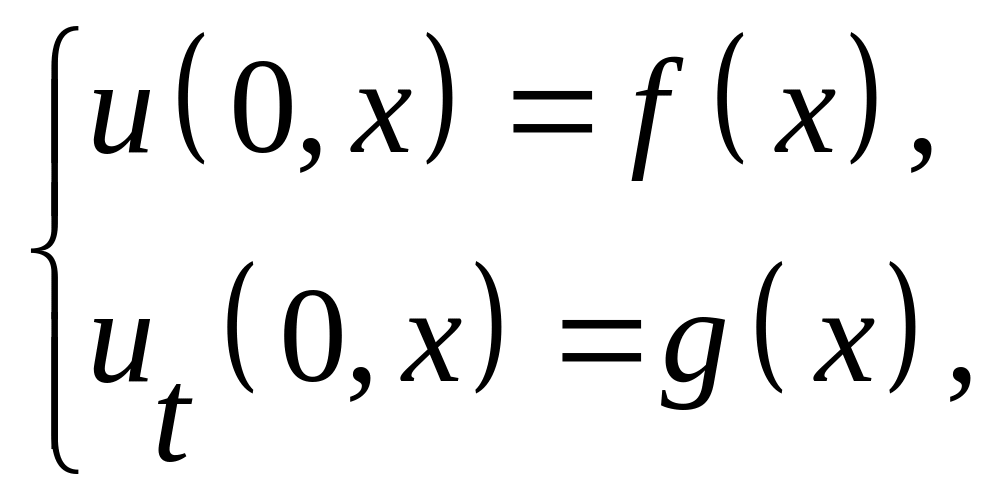
![]()
Розв’язування задачі розіб’ємо на кроки.
Крок
1. Заміна
координат t,
x
новими
канонічними координатами![]() ,
,![]() :
:
![]() ,які
зводять рівняння до вигляду
,які
зводять рівняння до вигляду
![]() .
.
Крок 2. Розв’язування перетвореного рівняння:
д![]() овільна
функція змінної
,
овільна
функція змінної
,![]() ,
,![]() .
.
Отже, загальний розв’язок рівняння записується у вигляді
.
Крок 3. Повернення до початкових координат t, x.
Для знаходження загального розв’язку рівняння (4) підставимо
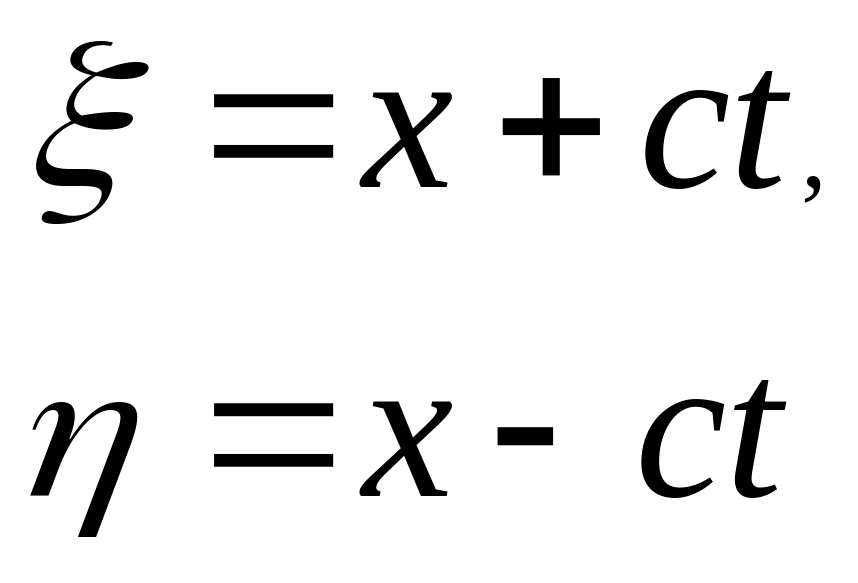
в розв’язок (5). В результаті отримаємо
![]()
Це загальний розв’язок рівняння (4
Крок 4. Врахування початкових умов.
Для розв’язування задачі Коші (4)
підставимо загальний розв’язок (6)
хвильового рівняння (який містить дві
довільні функції) в початкові умови,
щоб знайти конкретні вирази для функцій
![]() і
і
![]() .
Маємо:
.
Маємо:
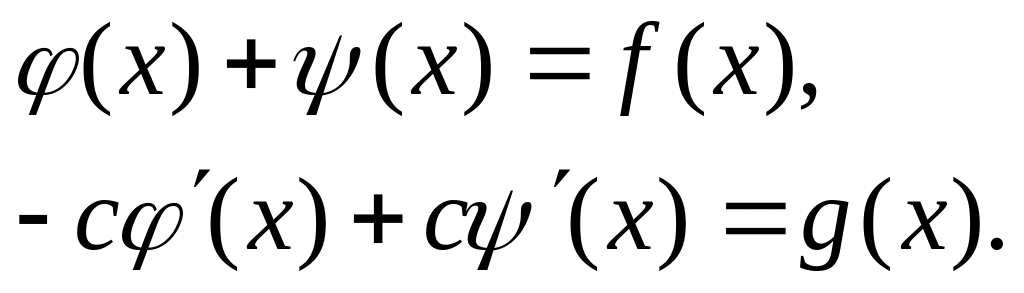
Проінтегрувавши
другу рівність в межах від
![]() до
до
![]() ,
отримаємо
,
отримаємо
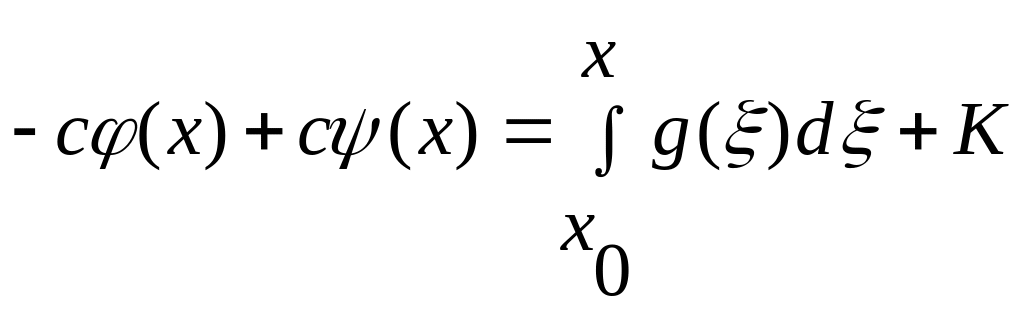
Тоді із (7) і (8) отримуємо
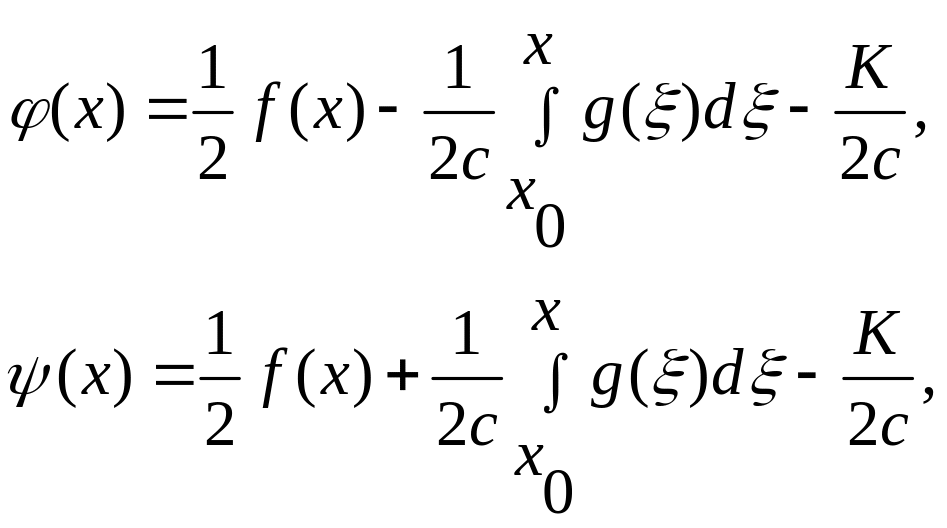
а тому
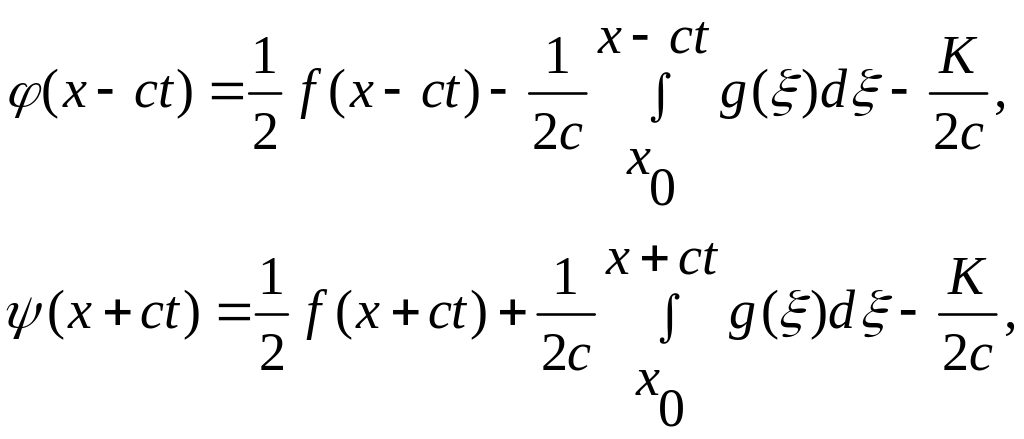 отже,
отже,
 .Розв’язок
називають формулою д’Аламбера.
.Розв’язок
називають формулою д’Аламбера.
6.Розв’язувння змінної задачі для напівнескінченної струни за допомогою формули д’аламбера
Поставимо перед собою задачу: знайти хвильові рухи напівнескінченної струни, лівий кінець якої жорстко закріплено при даних початкових умовах. Тут є додаткова гранична умова (ГУ), а тому задача має такий вигляд:
(ДРЧП)
![]() ,
,
(ГУ)
![]() ,
,
(ПУ)
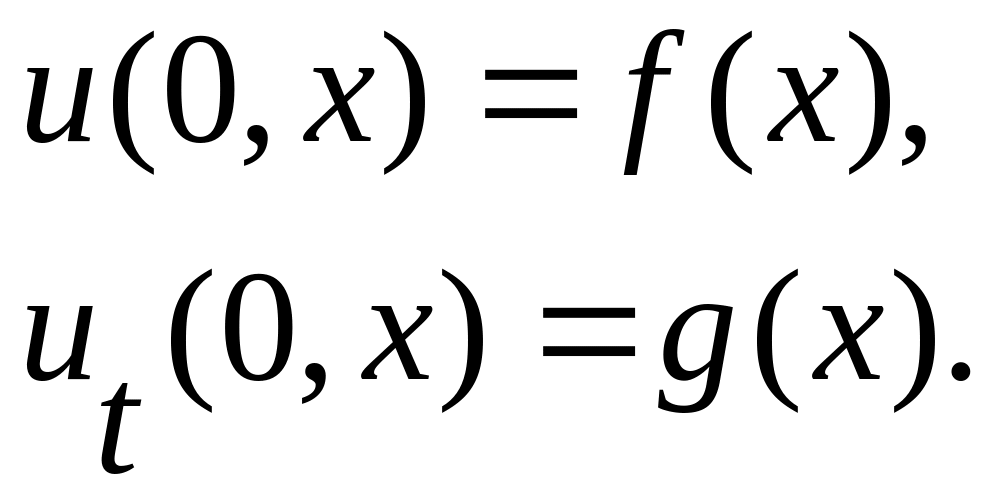
![]() .
.
Підставивши загальний розв’язок в початкові умови, маємо
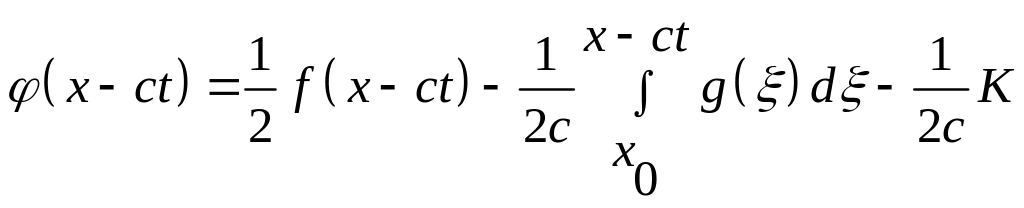
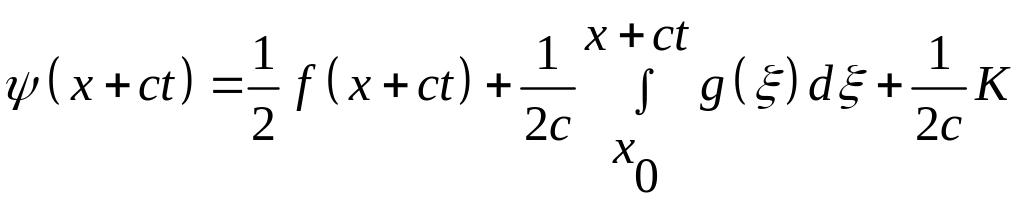 .
.
Тепер
виникає проблема, якої не було під час
розв’язування задачі Коші. Розв’язок
![]() повинен бути визначеним скрізь лише
всередині першого квадранта
повинен бути визначеним скрізь лише
всередині першого квадранта
![]() площини змінних
площини змінних
![]() .
Отже, ми повинні вміти обчислити значення
функції
.
Отже, ми повинні вміти обчислити значення
функції
![]() для всіх
для всіх
![]() а значення функції
а значення функції
![]() для всіх
для всіх
![]() .
.
На
жаль, перша з формул (11)
дозволяє
обчислювати
лише для
![]() ,
оскільки в початкових умовах функції
f(x)
та
g(x)
визначені лише для додатних значень
аргумента.
,
оскільки в початкових умовах функції
f(x)
та
g(x)
визначені лише для додатних значень
аргумента.
Якщо , то
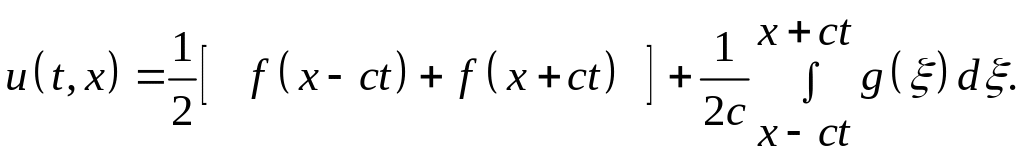
Що
робити, коли
![]() ?
Для цього скористаємося граничною
умовою
?
Для цього скористаємося граничною
умовою
![]() З її допомогою доозначимо функцію
для
.
Підставивши
З її допомогою доозначимо функцію
для
.
Підставивши
![]() в граничну умову отримаємо
в граничну умову отримаємо
![]() ,
звідки
,
звідки
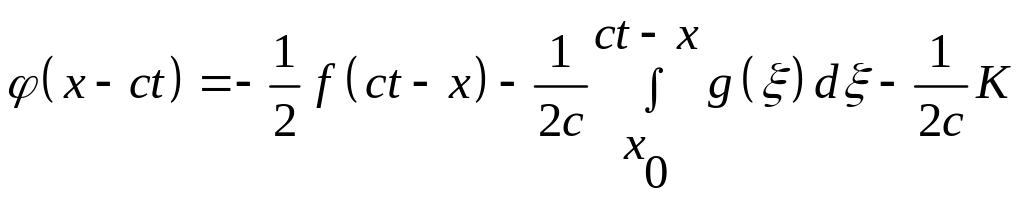 .
.
Підстановка знайденого значення в загальний розв’язок дає
 ,
,
![]()
Комбінуючи
розв’язки для
та
![]() ,
нарешті отримуємо
,
нарешті отримуємо
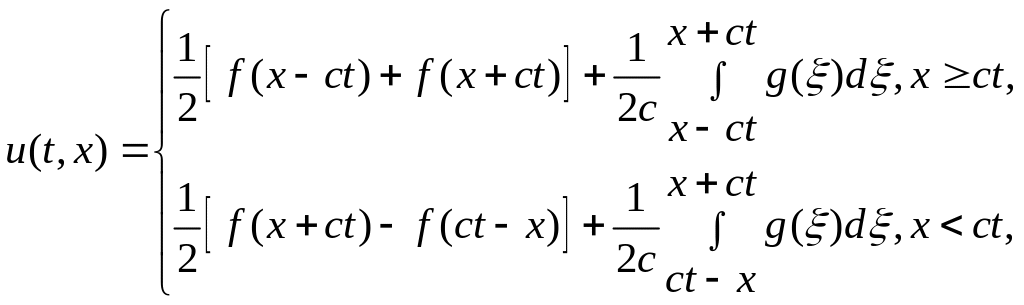 розв'язок
задачі.
розв'язок
задачі.
7. Коливання обмеженої струни (стоячі хвилі)
Розглянемо,
випадок, коли гітарну струну, яка
закріплена в точках
![]() ,
,
![]() ,
привести в рух, для цього розв’яжемо
таку крайову задачу гіперболічного
типу:
,
привести в рух, для цього розв’яжемо
таку крайову задачу гіперболічного
типу:
(ДРЧП)
![]() ,
0< x
<L,
0< t
<∞;
,
0< x
<L,
0< t
<∞;
(ГУ)
![]() 0< t
<∞;(ПУ)
0< t
<∞;(ПУ)
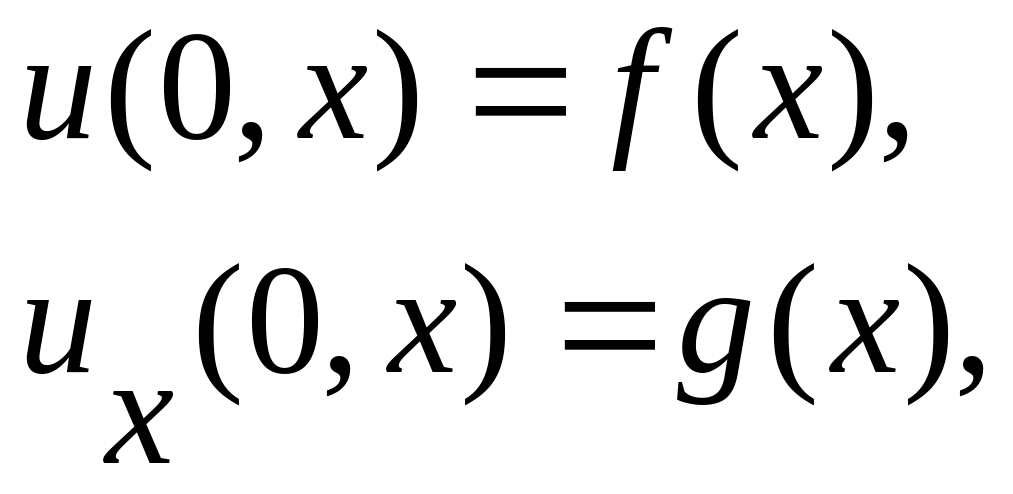 0≤ x
≤L.
0≤ x
≤L.
Виявляється, у цьому випадкові біжучі хвилі відбиваються від меж так, що результуючі коливання стають не біжучими, а такими, які зберігають форму в одному положенні, тобто перетворюються в стоячі хвилі.
Знайдемо спочатку стоячі хвилі, тобто розв'язки вигляду
![]()
Підставивши і відокремивши змінні, отримуємо два звичайних диференціальних рівняння
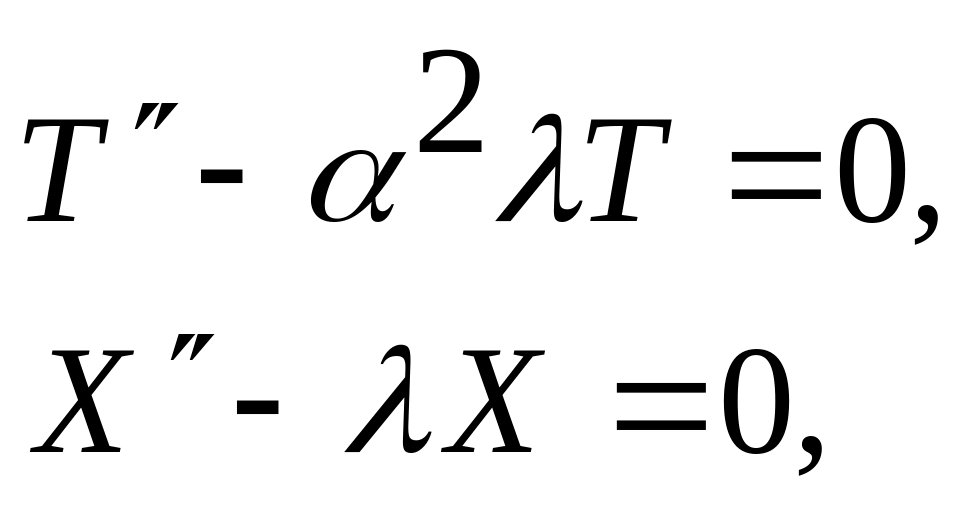 де
стала –∞<
де
стала –∞<
![]() <+∞.
<+∞.
В
залежності від значень
![]() маємо такі розв'язки рівнянь:
маємо такі розв'язки рівнянь:
<
0,
![]() :
:
![]()
= 0,
![]()
>
0,
![]() :
:
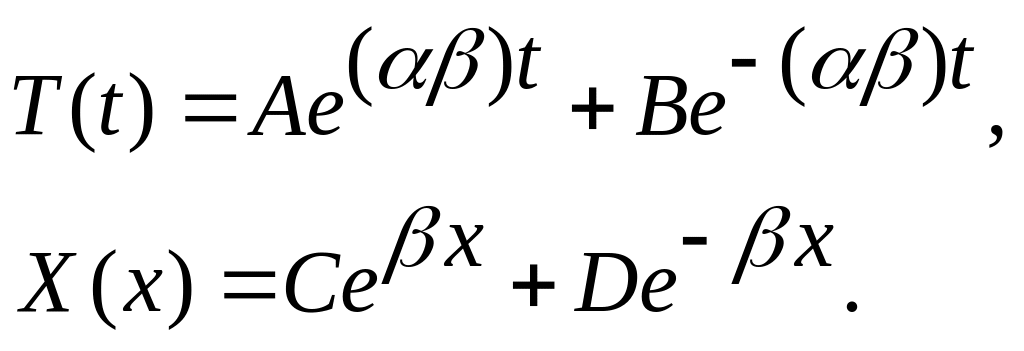 Задовольняють
лише розв'язки, які відповідають
Задовольняють
лише розв'язки, які відповідають
![]()
![]()
Знайдемо
A,
B,
C,
D
та
,
які задовольняють Г. У.
![]()
![]()
![]()
![]() .
.
Отже,
константа відокремлення
![]() (замість
ми шукаємо її) повинна задовольняти
рівняння
(замість
ми шукаємо її) повинна задовольняти
рівняння
![]() ,
звідки випливає
,
звідки випливає
![]() ,
n
=1,
2, ... .
,
n
=1,
2, ... .
Отже, послідовність елементарних коливань струни має вигляд
![]()
де an , bn – довільні дійсні сталі.
Підстановка в початкові умови дає
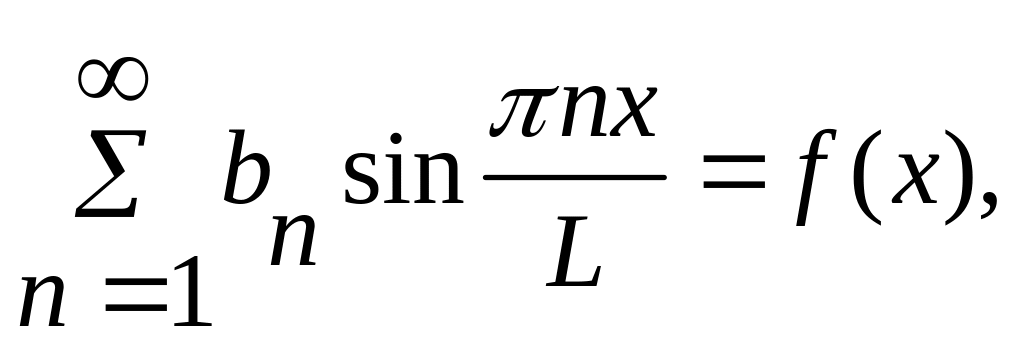
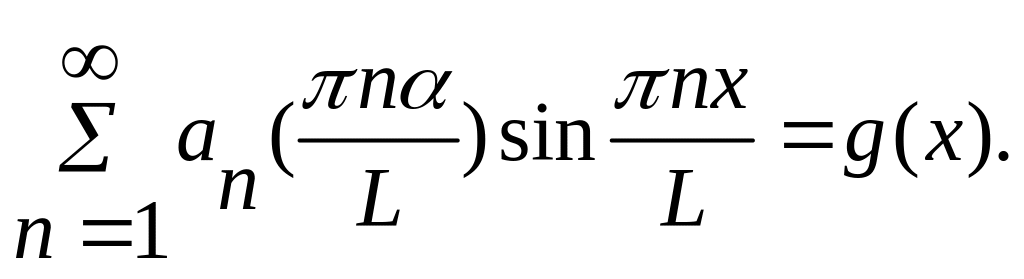
Скориставшись співвідношеннями ортогональності
знаходимо
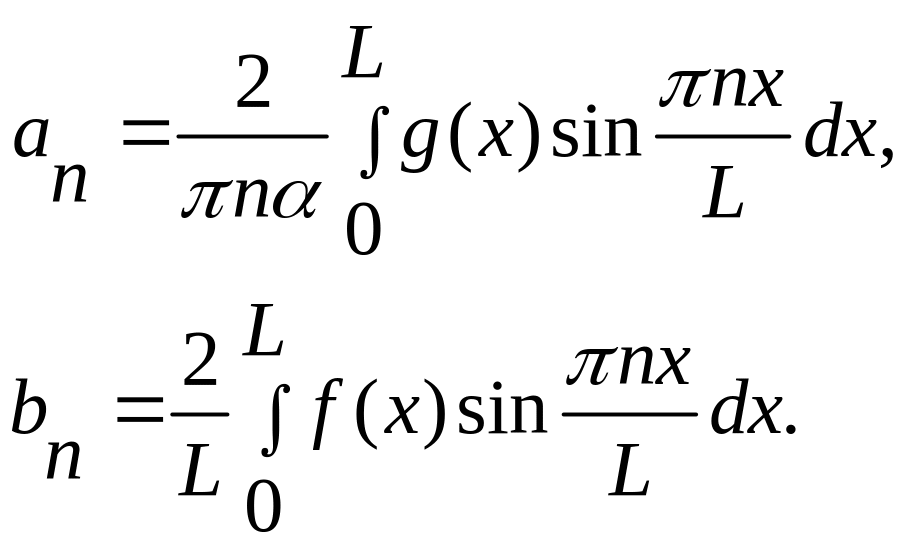
Отже, задача розв’язана. Її розв'язок має вигляд
![]()
