
- •Глава . Криволинейные интегралы § .1 Криволинейный интеграл 1-го рода (по длине дуги)
- •§ .2 Свойства криволинейного интеграла I рода
- •4. Геометрический смысл криволинейного интеграла I рода:
- •5. Физический смысл криволинейного интеграла I рода:
- •§ .3 Вычисление криволинейного интеграла I рода
- •§ .5 Свойства криволинейного интеграла II рода.
- •§ .6 Вычисление криволинейного интеграла II рода
- •§ .7 Механический смысл криволинейного интеграла II-го рода
- •§ .8 Формула Остроградского-Грина
- •§ .9 Независимость криволинейного интеграла II рода от пути интегрирования
Глава . Криволинейные интегралы § .1 Криволинейный интеграл 1-го рода (по длине дуги)
Def : Пусть в пространстве R3 кривая L задана параметрически:
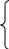 x=x(t)
x=x(t)
y=y(t) (1)
z=z(t), где a ≤t ≤b
Если x(t),y(t),z(t) –непрерывны, то они определяют непрерывную кривую L, если также непрерывны производные этих функций на [a, b], которые одновременно не обращаются в нуль, то кривая L называется гладкой.
Def : Гладкая на [a, b] кривая L, определяемая уравнениями (1) спрямляема, если существует предел длин ломаных, вписанных в кривую. Этот предел называется длиной кривой L .
Рассмотрим в пространстве R3 некоторую гладкую кривую AB, в каждой точке которой задана функция u= f(x,y,z):
1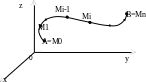 .
Разобьем AB
на n
частичных дуг точками A=M0,
M1,…,Mn=B.
Обозначим
∆li
–
длина дуги Mi-1Mi,
i=
.
Разобьем AB
на n
частичных дуг точками A=M0,
M1,…,Mn=B.
Обозначим
∆li
–
длина дуги Mi-1Mi,
i=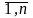 ,
λ=max{∆li
}.
,
λ=max{∆li
}.
2. На каждой из частичных дуг выберем некоторую т. Ni (ξi ,ηi ,ζi), i= . Вычислим f (Ni) = f (ξi ,ηi ,ζi).
3.
Найдем произведения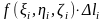 ,
i=
.
,
i=
.
4.
Составим сумму этих произведений
 -
-
интегральная сумма I рода для функции f(x,y,z) по длине дуги AB.
5. Если существует конечный предел интегральной суммы I рода при λ→0, который не зависит ни от способа разбиения дуги AB на частичные дуги, ни от выбора в каждой из них т. Ni, то он называется криволинейным интегралом от функции f(x,y,z) по длине дуги AB или криволинейным интегралом I рода и обозначается @
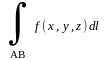 =
=
Замечание. Если кривая AB лежит в плоскости, то криволинейный интеграл имеет вид @
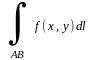 =
=
Теорема существования криволинейного интеграла I рода.
Если функция f(x,y,z) непрерывна на гладкой кривой AB, то криволинейный интеграл по длине дуги AB существует.
§ .2 Свойства криволинейного интеграла I рода
@
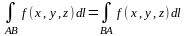
( Длина дуги ∆li не зависит от того, какая из точек Mi-1 или Mi принята за её начало, а какая за конец .)
2. Линейность. Если для функций f1(x,y,z) и f2(x,y,z) существуют криволинейные интегралы по дуге AB, то для функции c1f1(x,y,z)+c2f2(x,y,z) также существует криволинейный интеграл по дуге AB, причем:
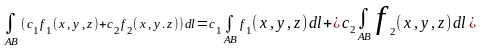
Частные случаи:
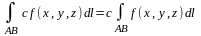
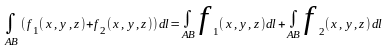
3. Аддитивность. Если дуга AB составлена из дуг AC и CB и для функции и=f(x,y,z) существует криволинейный интеграл по дуге AB, то для этой функции существуют криволинейные интегралы по дугам AC и CB, причем:
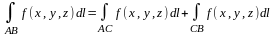
4. Геометрический смысл криволинейного интеграла I рода:
Если
f(x,y,z)=1,
то
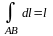 - длина
дуги кривой AB.
- длина
дуги кривой AB.
5. Физический смысл криволинейного интеграла I рода:
Пусть AB – материальная кривая, имеющая плотность ρ(x,y,z), тогда
 -
масса материальной кривой.
-
масса материальной кривой.
§ .3 Вычисление криволинейного интеграла I рода
Вычисление криволинейных интегралов по длине дуги ( I рода) производится путем преобразования их в определенные интегралы.
1. Кривая интегрирования AB задана параметрическими уравнениями.
а )
AB
– плоская
гладкая кривая задана как:
x=x(t)
)
AB
– плоская
гладкая кривая задана как:
x=x(t)
@ y=y(t), a ≤t ≤b
- дифференциал
длины дуги, заданной параметрически.
б )
AB
–
пространственная
гладкая кривая задана как:
x=x(t)
)
AB
–
пространственная
гладкая кривая задана как:
x=x(t)
y=y(t),
z=z(t), a ≤t ≤b
@
2. Кривая интегрирования AB задана явным образом: y=y(x), где a ≤ x ≤ b
@
§ .4 Криволинейный интеграл 2-го рода (по координатам)
Рассмотрим
в пространстве R3
гладкую
кривую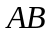 ,
во всех точках которой определены
функции
,
во всех точках которой определены
функции
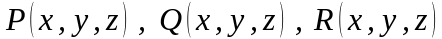
Разобьем дугу на
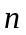 частичных дуг точками
частичных дуг точками
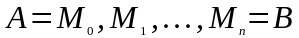
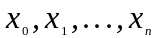 -
абсциссы точек деления,
-
абсциссы точек деления,

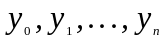 -
ординаты точек деления,
-
ординаты точек деления,
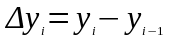
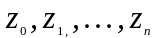 -
аппликаты точек деления,
-
аппликаты точек деления,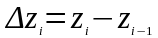 ,где
,где
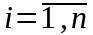
2.
На каждой частичной дуге выберем
произвольную точку
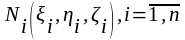 и вычислим
и вычислим
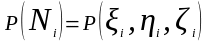
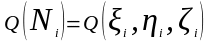

3. Найдём произведения
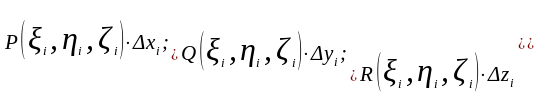 ,
где
,
где

4.
Составим сумму: 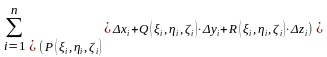 -
интегральная сумма по координатам или
интегральная
сумма II
рода
для вектор-функции @
-
интегральная сумма по координатам или
интегральная
сумма II
рода
для вектор-функции @
5.
Если
существует предел интегральной суммы
II
рода при
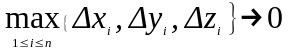 ,
не зависящий ни от способа разбиения
дуги
на частичные дуги, ни от выбора точек
,
не зависящий ни от способа разбиения
дуги
на частичные дуги, ни от выбора точек
 на каждой из них, то он называется
криволинейным
интегралом по координатам от функций
на каждой из них, то он называется
криволинейным
интегралом по координатам от функций
 по
дуге
или
криволинейным
интегралом II
рода и
обозначается @
по
дуге
или
криволинейным
интегралом II
рода и
обозначается @
-
линия интегрирования,
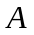 -начальная,
-начальная,
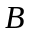 -конечная
точки интегрирования.
-конечная
точки интегрирования.
Замечания.
1.
Если кривая
плоская,
т.е. лежит в плоскости
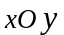 ,
то криволинейный интеграл примет вид:
@
,
то криволинейный интеграл примет вид:
@
- криволинейный интеграл II рода в плоскости .
2.
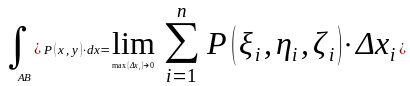 -
криволинейный интеграл
II
рода по координате
-
криволинейный интеграл
II
рода по координате
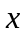 .
.
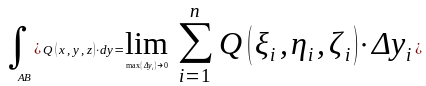 -
криволинейный интеграл II
рода по координате
-
криволинейный интеграл II
рода по координате
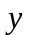 .
.
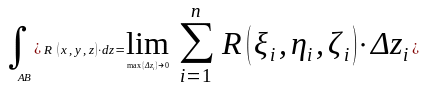 -
криволинейный интеграл II
рода по координате
-
криволинейный интеграл II
рода по координате
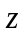 .
.
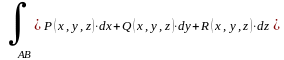 -
общий (полный) криволинейный интеграл
II
рода в пространстве R3
.
-
общий (полный) криволинейный интеграл
II
рода в пространстве R3
.
Теорема существования криволинейного интеграла II рода.
Если
функции
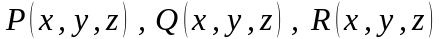 непрерывны в точках гладкой кривой
,
то предел интегральной суммы II
рода существует, т.е. существует
криволинейный интеграл II
рода.
непрерывны в точках гладкой кривой
,
то предел интегральной суммы II
рода существует, т.е. существует
криволинейный интеграл II
рода.
