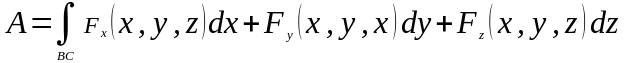- •Глава . Криволинейные интегралы § .1 Криволинейный интеграл 1-го рода (по длине дуги)
- •§ .2 Свойства криволинейного интеграла I рода
- •4. Геометрический смысл криволинейного интеграла I рода:
- •5. Физический смысл криволинейного интеграла I рода:
- •§ .3 Вычисление криволинейного интеграла I рода
- •§ .5 Свойства криволинейного интеграла II рода.
- •§ .6 Вычисление криволинейного интеграла II рода
- •§ .7 Механический смысл криволинейного интеграла II-го рода
- •§ .8 Формула Остроградского-Грина
- •§ .9 Независимость криволинейного интеграла II рода от пути интегрирования
§ .5 Свойства криволинейного интеграла II рода.
Пусть P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z) непрерывны на гладкой кривой AB.
@
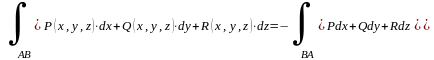
Доказательство:
Знаки
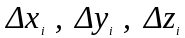 изменяются на противоположные, =>
интегральная сумма изменяет знак, =>
предел, т.е. криволинейный интеграл,
изменяет знак.
изменяются на противоположные, =>
интегральная сумма изменяет знак, =>
предел, т.е. криволинейный интеграл,
изменяет знак.
2.
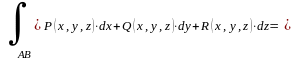
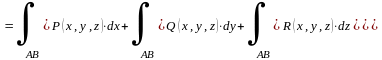
Доказательство cледует из определения и свойств предела.
3-4. Свойство линейности и свойство аддитивности аналогичны свойствам криволинейного интеграла I рода.

Аддитивность:
если кривая
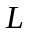 разбита на части l1
и
l2,
то
разбита на части l1
и
l2,
то
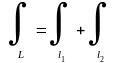
Замечание. Пусть кривая замкнута, т.е. точка совпадает с точкой .
Обозначим эту замкнутую кривую через L, тогда криволинейный интеграл II рода по замкнутой кривой обозначается @
Выбор начальной точки, которая является и конечной, роли не играет.
Направление обхода называют положительным, если область, ограниченная контуром, при обходе остаётся слева, т.е. обход совершается против часовой стрелки.
Направление обхода контура в противоположном направлении, т.е. по часовой стрелке называют отрицательным.
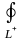 -
положительное направление, @
-
положительное направление, @
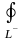 -
отрицательное направление @
-
отрицательное направление @
При этом интегралы отличаются знаком, т.е. @
Если направление обхода не указано, то замкнутый контур обходится в положительном направлении.
§ .6 Вычисление криволинейного интеграла II рода
1. Кривая - пространственная гладкая кривая, заданная параметрическими уравнениями:
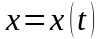
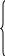
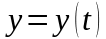
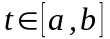 Начальной
точке
соответствует
Начальной
точке
соответствует
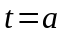
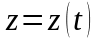 Конечной
точке
соответствует
Конечной
точке
соответствует
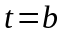
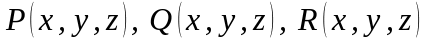 -
непрерывные во всех точках
,
-
непрерывные во всех точках
,
 .
@
.
@
Кривая - гладкая плоская кривая, заданная параметрическими уравнениями:
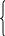
.
Точке соответствует , точке соответствует ,
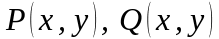 -
непрерывны во всех точках кривой
.
Произведём замену
-
непрерывны во всех точках кривой
.
Произведём замену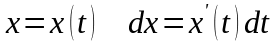
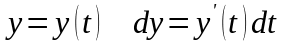 @
@
3.
Кривая
задана явным уравнением
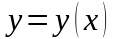 ,
где
,
где
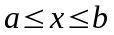
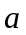 -
абсцисса точки
,
-
абсцисса точки
,
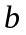 - абсцисса точки
.
- абсцисса точки
.
Заменим
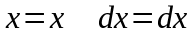 (
-
параметр)
(
-
параметр)
 @
@
Вывод: @
§ .7 Механический смысл криволинейного интеграла II-го рода
Пусть
точка
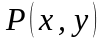 движется вдоль некоторой плоской линии
от точки
к точке
движется вдоль некоторой плоской линии
от точки
к точке
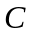 .
К точке
.
К точке
 приложена сила
приложена сила
 ,
которая меняется по величине и направлению
при перемещении точки
,
т.е. является функцией координат точки
:
,
которая меняется по величине и направлению
при перемещении точки
,
т.е. является функцией координат точки
:
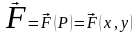
Сила задана своими проекциями на координатные оси
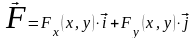 ,
где
,
где
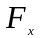 -
проекция
на
-
проекция
на
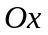 ,
,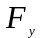 -
проекция
на
-
проекция
на
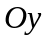 .
.
Работа силы при перемещении точки из точки в точку равна:
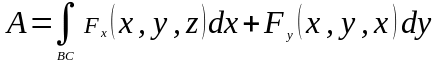 -
работа силы
вдоль кривой
-
работа силы
вдоль кривой
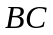 .
.
Замечание.
Если
точка
движется вдоль пространственной кривой
от точки
к точке
и на
действует сила
,
заданная проекциями
 этой силы на координатные оси, то работа
определяется
по формуле:
этой силы на координатные оси, то работа
определяется
по формуле: