ВВЕДЕНИЕ

Система программирования Турбо Паскаль представляет собой единство двух в известной степени самостоятельных начал: компилятора с языка программирования Паскаль (язык назван в честь выдающегося французского математика и философа Блеза Паскаля (1623-1662)) и некоторой инструментальной программной оболочки, способствующей повышению эффективности создания программ. Для краткости условимся в дальнейшем называть реализуемый компилятором язык программирования Паскаль - языком Турбо Паскаля, а разнообразные сервисные услуги, представляемые программной оболочкой, - средой Турбо Паскаля.

Общие понятия и правила программирования на языке Турбо Паскаль

Программа составляется из операторов Турбо Паскаля, которые разделяются символом ";".

В языке Turbo Pascal для сравнения переменных, принимающих численные значения, существуют следующие операции отношений:

< меньше,

<= меньше или равно,

= равно,

<> не равно,

> больше,

>= больше или равно.

Язык TP может обрабатывать не только числа, но и символы.

1 ПРОГРАМИРОВАНИЕ

1.1.Линейная регрессия. Использование метода наименьших квадратов (МНК).

Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Выбрав вид функции регрессии, т.е. вид рассматриваемой модели зависимости Y от Х (или Х от У), например, линейную модель y=a+bx, необходимо определить конкретные значения коэффициентов модели. При различных значениях а и b можно построить бесконечное число зависимостей вида y=a+bx, т. е на координатной плоскости имеется бесконечное количество прямых, нам же необходима такая зависимость, которая соответствует наблюдаемым значениям наилучшим образом. Таким образом, задача сводится к подбору наилучших коэффициентов.

Линейную функцию a+bx ищем, исходя лишь из некоторого количества имеющихся наблюдений. Для нахождения функции с наилучшим соответствием наблюдаемым значением используем метод наименьших квадратов. Постараемся сделать это приближение наилучшим. Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонений, реальных значений от, расположенных на прямой. Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.

Находим коэффициенты а и b так, чтобы сумма квадратов отклонений наблюдаемых значений от значений на прямой линии регрессии оказалась наименьшей:

S→min;

S = ∑(yi – Yi)2 = ∑(yi – a – bxi)2→ min;

Исследуя на экстремум эту функцию аргументов а и с помощью производных, можно доказать, что функция принимает минимальное значение, если коэффициенты а и b являются решениями системы:

1.2. Метод половинного деления.

Метод половинного деления или дихотомии при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется.

Метод половинного деления является самым простейшим из методов уточнения корней, предназначенный для нахождения корней уравнений, представленных в виде f(x)=0. Этот метод решения уравнений отличается от выше рассмотренных методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, (рис. 1), тогда на отрезке имеется хотя бы один корень.

Возьмем середину отрезка с = (a+b)/2. Если f(a)*f(c) < 0, то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b.

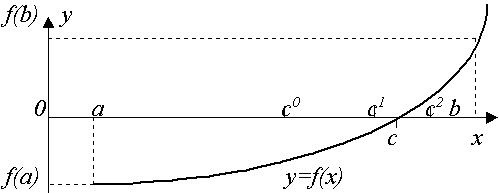
Рисунок 1 – Графическая иллюстрация метода половинного деления

Рис. 2. Блок-схема метода половинного деления

Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (b-a)<ε.

1.3. Вычисление определенных интегралов. Метод трапеций.

Необходимость в вычислении определенных интегралов с использованием численных методов возникает, в основном, в двух случаях. Во-первых, подынтегральная функция может быть задана таблично, например, как полученная в результате каких-либо измерений. Во-вторых, первообразная не может быть найдена в аналитическом виде, то есть, интеграл не является табличным. Как и все вычислительные методы, численное интегрирование является приближенным, и интеграл может быть получен с заданной точностью. Метод трапеций обычно даёт более точное значение интеграла, чем метод прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций и приближённое значение определённого интеграла находится как сумма площадей трапеций.Простейшим методом численного интегрирования является МЕТОД ТРАПЕЦИЙ. Речь идет о вычислении интеграла:

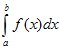
Метод применим, если пределы интегрирования конечны, а подынтегральная функция не имеет особенностей, хотя несложная предварительная процедура деления интервала интегрирования на несколько частей позволяет применить эту методику и к интегрированию функции, имеющей конечное число разрывов первого рода. В методе трапеций интервал [a,b] разбивается на n элементарных отрезков длиной:

точками с координатой:

Пусть требуется вычислить площадь S «криволинейной трапеции» (см. рис.), ограниченной дугой непрерывной линии, уравнение которой у = f (x). Для вычисления площади S этой криволинейной трапеции основание (отрезок [a, b]) разбивают на n участков (необязательно равных) точками а = x0 < x1 < ... < xn-1 < < xn = b, обозначая длины этих участков h, на каждом таком участке строят прямоугольники с высотами f (x1), f (x2), ..., f (xn) где xk — некоторая точка из отрезка [xk - 1, xk]. Выражение для площади криволинейной трапеции тем точнее, чем меньше длины h участков разбиения. Для нахождения точного значения площади S надо найти предел сумм Sn в предположении, что число точек деления неограниченно увеличивается и наибольшая из длин h стремится к нулю.

На каждом из элементарных отрезков подынтегральная функция заменяется линейной функцией, а соответствующий участок площади под кривой y=f(x) заменяется трапецией так, как это показано на рис.

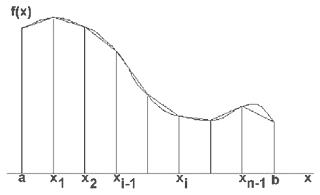
Рисунок 2 – Интегрирование методом трапеций

S тр = SУ0У1У2 …Уn

∑Sтр = S1 +S2 + S3 … +Sn

S1 = (у0+у1)/2*h

S2 = (у1+у2)/2*h

Sn = (уn-1+ уn)/2*h

∑S = h((у0+уn)+у1+у2+у3+ …уn-1)

∑S = h ((f(a) + f(b))/2 +∑уi)