Задание 1 (№10)

Из 36 телевизоров, имеющихся в магазине, 8 единиц произведено заводом А, 11 единиц – заводом Б и 17 единиц заводом В. Вероятность того, что телевизор, изготовленный заводами А, Б и В, в течение гарантийного срока не выйдет из строя, соответственно равна 0,98; 0,92; 0,88. Найти вероятность того, что наудачу взятый телевизор выдержит гарантийный срок.

Решение:

Введем обозначения:

событие А – «телевизор выдержал гарантийный срок»;

гипотеза Н₁ - «телевизор, выдержавший гарантийный срок, произведен на заводе А»

гипотеза Н₂ - «телевизор, выдержавший гарантийный срок, произведен на заводе Б»

гипотеза Н₃ - «телевизор, выдержавший гарантийный срок, произведен на заводе В»

В соответствии с условием задачи:

Р(А/Н₁)=0,98

Р(А/Н₂)=0,92

Р(А/Н₃)=0,88

Р(Н₁)=8/36

Р(Н₂)=11/36

Р(Н₃)=17/36

В соответствии с формулой полной вероятности, получаем:

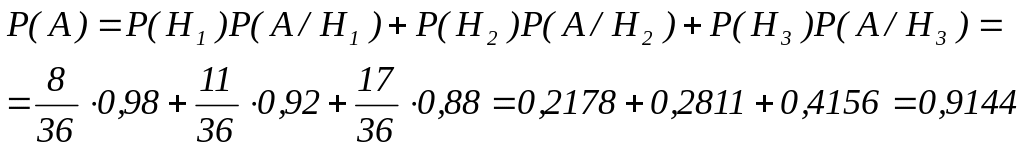
Ответ: .

Задание 2 (№30)

В некотором населенном пункте 60% мужчин имеют автомобили. Для некоторых исследований случайным образом отбираются 8 мужчин. Определить

а) вероятность того, что в выборке окажутся 4 мужчины с автомобилями

б) вероятность того, что в выборке окажутся не менее пяти мужчин с автомобилями.

Решение:

Искомые вероятности находим с помощью формулы Бернулли.

а) n=8; k=4; р=0,6; q=1-р=1-0,6=0,4

поэтому

.

Таким образом, вероятность того, что в выборке окажутся 4 мужчины с автомобилями равна

б) Событие А – «вероятность того, что в выборке окажутся не менее пяти мужчин с автомобилями», состоит в том, что из 8-ми мужчин имеют автомобиль или 5, или 6, или 7, или 8.

По формуле Бернулли и по теореме сложения вероятностей, получаем:

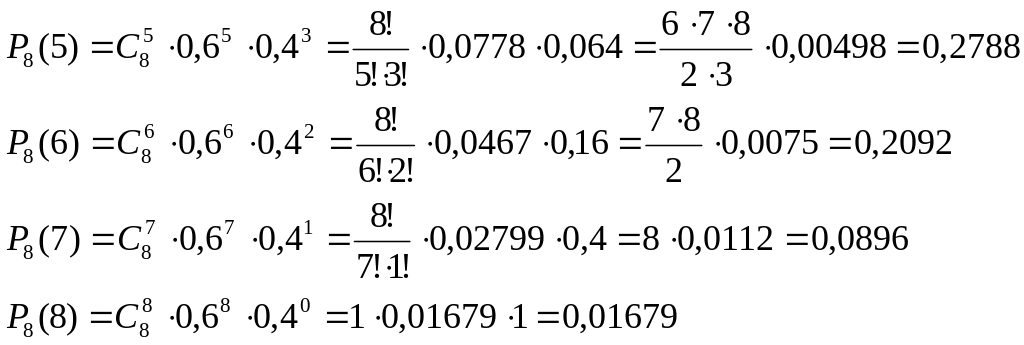
Значит

Ответ:

Задание 3 (№50)

Заводом выпущено n=4 компрессора. Составить закон распределения СВ Х – числа компрессоров, соответствующим техническим требованиям заказчика, построить многоугольник распределения этой СВ. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение, если вероятность того, что любой отдельно взятый компрессор соответствует техническим требованиям заказчика равна р=0,65.

Решение:

Случайная величина Х может принимать значения: 0, 1, 2, 3, 4.

По условию вероятность того, что любой отдельно взятый компрессор соответствует техническим требованиям заказчика равна р=0,65.

Значит q=1-0,65=0,35.

С помощью формулы Бернулли, находим:

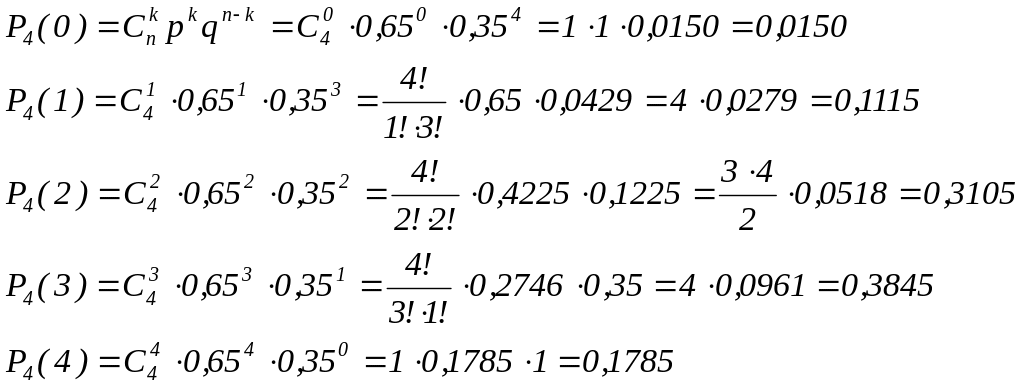
Следовательно закон распределения СВ Х можно записать в виде таблицы:

Х	0	1	2	3	4	Сумма
Р	0,0150	0,1115	0,3105	0,3845	0,1785	1

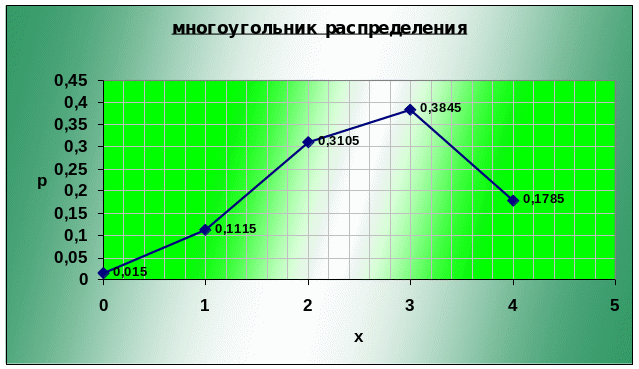
В прямоугольной декартовой системе координат строим точки . И соединяем их последовательно отрезками прямых.

Математическое ожидание вычисляем по формуле:

Значит,

Дисперсию вычислим по формуле:

Вычислим сначала

Значит,

Среднее квадратическое отклонение вычислим по формуле: .

Значит

Ответ: , , .

Задание 4 (№70)

Масса ягод является случайной величиной, распределенной по нормальному закону с математическим ожиданием а=22 и средним квадратическим отклонением . Ягоды с массой от 12 до 20 г относят к средней категории, с массой более 20 г - к высшей категории.

Определить:

1. проценты ягод средней и высшей категории;

2. величину, которую не превзойдет масса ягод с вероятностью р=0,96.

Решение:

1. Для вычисления процента ягод средней и высшей категории воспользуемся формулой, по которой найдем вероятность попадания нормальной СВ Х в интервал :

где Ф(х) - функция Лапласа.

Значит вероятность того, что масса ягод находится в интервале от 12 до 20 г равна:

По таблице значений функции Лапласа находим:

, .

Значит,

Таким образом, ягод средней категории, т.е. с массой от 12 до 20 г нет

Вероятность того, что масса ягод находится в интервале от 20 г и выше равна:

По таблице значений функции Лапласа находим:

, .

Значит,

Таким образом, процент ягод высшей категории, т.е. с массой более 20 г равен 100%.

2. Для того, чтобы найти величину, которую не превзойдет масса ягод с вероятностью р=0,96, воспользуемся формулой:

По условию известно, что а=22 и .

Так как

Значит, по таблице значений функции Лапласа находим, что . Следовательно, .

Из неравенства , получаем

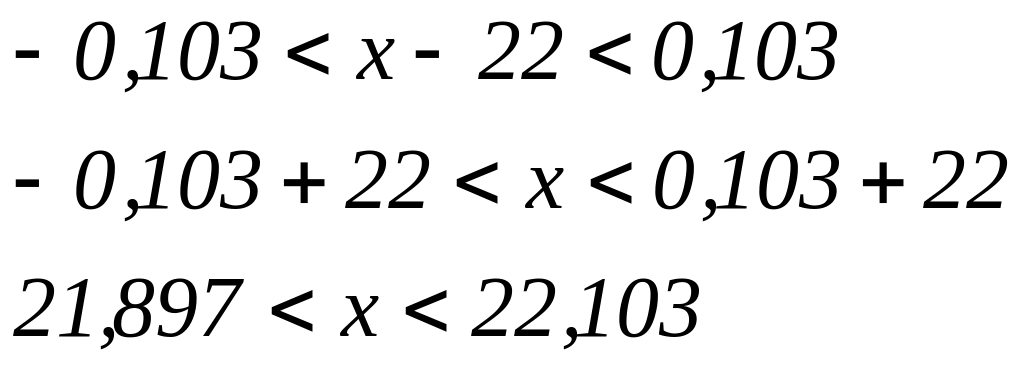
Значит, масса ягод не превзойдет величины 22,103 г

Ответ: 1) ягод средней категории нет, все относятся к высшей категории, 100%;

2) масса ягод не превзойдет величины 22,103г, с вероятностью р=0,96.

Задание 5 (№11)

В сборочный цех завода поступают детали из трех экспериментальных цехов. Первый экспериментальный цех дает 2,5% брака, второй – 1,5%, третий – 1%. Определить вероятность попадания на сборку небракованной детали, если из каждого экспериментального цеха в сборочный цех поступило соответственно 700, 450 и 280 деталей.

Решение:

Введем обозначения:

событие А – «на сборку попала небракованная деталь»;

событие – «на сборку попала бракованная деталь»;

гипотеза Н₁ - «деталь произведена 1-ым экспериментальным цехом»

гипотеза Н₂ - «деталь произведена 2-ым экспериментальным цехом»

гипотеза Н₃ - «деталь произведена 3-им экспериментальным цехом»

В соответствии с условием задачи:

Р( /Н₁)=0,025

Р( /Н₂)=0,015

Р( /Н₃)=0,01

В соответствии с формулой полной вероятности, получаем:

Следовательно,

Ответ: - вероятность того, что на сборку попадет небракованная деталь.

Задание 6 (№31)

Вероятность того, что расход воды на заводе в течение дня окажется не превышающим норму, равна 0,75. Найти вероятность того, что расход воды будет нормальным в течение не менее 6 из ближайших 9 дней.

Решение:

Искомые вероятности находим с помощью формулы Бернулли: .

Пусть событие А – «вероятность того, что расход воды будет нормальным в течение не менее, чем 6 из ближайших 9 дней», состоит в том, что из 9-и дней расход воды будет нормальным в течение или 6, или 7, или 8, или 9 дней.

n=9; k=6, 7, 8, 9; р=0,75; q=1-р=1-0,75=0,25

По формуле Бернулли

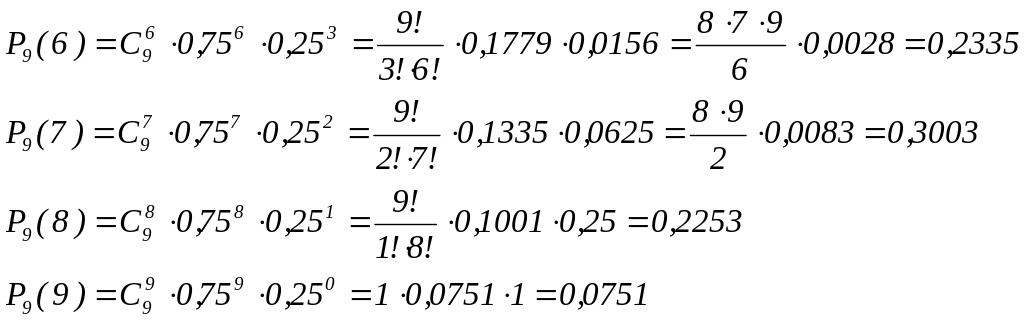
Значит, по теореме сложения вероятностей, получаем:

Ответ: вероятность того, что расход воды будет нормальным в течение не менее 6 из ближайших 9 дней равна

Задание 7 (№51)

Некоторый предприниматель построил по одной заправочной станции в n=4 города. Вероятность того, что за текущий год предприниматель получит прибыль с каждой заправочной станции, равна р=0,50.

Составить закон распределения СВ Х - числа заправочных станций, по которым предприниматель получит прибыль, построить многоугольник распределения этой СВ. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой СВ.

Решение:

Случайная величина Х может принимать значения: 0, 1, 2, 3, 4.

По условию вероятность того, что владелец заправочной станции получит прибыль, равна p=0,50. Значит q=1-0,50=0,50.

С помощью формулы Бернулли, находим:

Следовательно закон распределения СВ Х можно записать в виде таблицы:

Х	0	1	2	3	4	Сумма
Р	0,0625	0,25	0,375	0,25	0,0625	1

В прямоугольной декартовой системе координат строим точки . И соединяем их последовательно отрезками прямых.

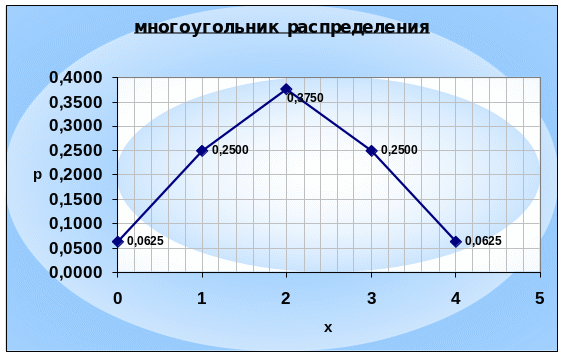
Математическое ожидание вычисляем по формуле:

Значит,

Дисперсию вычислим по формуле:

Вычислим сначала

Значит,

Среднее квадратическое отклонение вычислим по формуле: .

Значит

Ответ: , , .

Задание 8 (№71)

Завод изготавливает детали, фактический размер которых является СВ, распределенной по нормальному закону с математическим ожидание а=18мм (проектный размер детали) и средним квадратическим отклонением мм. Годными считаются детали, размер которых заключен между 16 и 19 мм. Определите:

1. процент бракованных деталей;

2. процент деталей, диаметр которых отличается от проектного на величину не превышающую

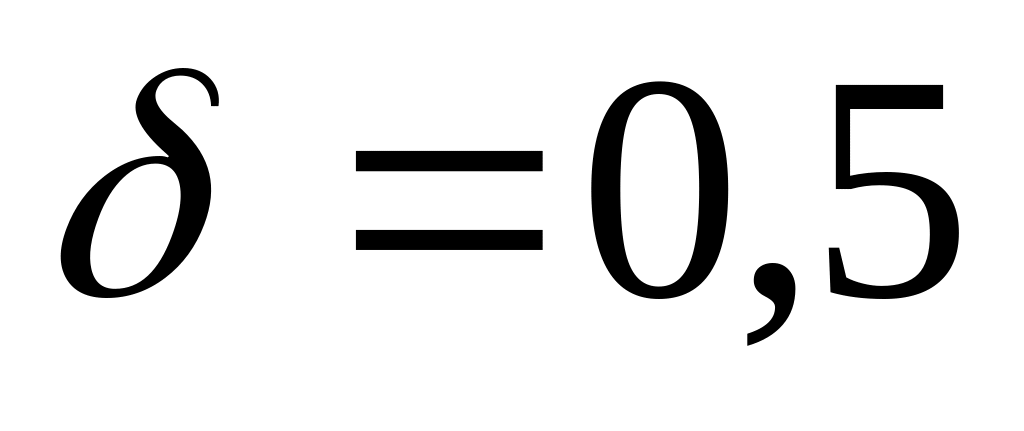
Решение:

1. найдем процент бракованных деталей.

Но сначала найдем вероятность попадания СВ в интервал от 16 до 19 мм по формуле:

где Ф(х) - функция Лапласа.

Значит:

По таблице значений функции Лапласа находим:

, .

Значит,

Значит процент годных деталей, равен 83,4%.

Следовательно, процент бракованных деталей составит:

100%-83,4%=16,6%

2) Для того, чтобы найти процент деталей, диаметр которых отличается от проектного на величину не превышающую , воспользуемся формулой:

По условию, , то искомая вероятность равна:

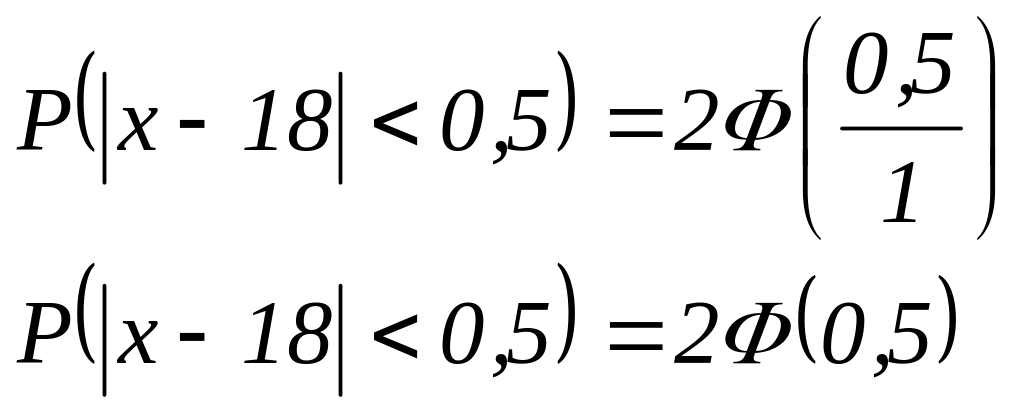
По таблице значений функции Лапласа находим: ,

Значит,

Следовательно, процент деталей, диаметр которых отличается от проектного а=18 на величину не превышающую равен 38,30%

Ответ: 1) процент бракованных деталей равен 16,6%;

2) процент деталей, диаметр которых отличается от проектного

3) на величину не превышающую равен 38,3%

Задание 9

Даны результаты продажи обуви за день в зависимости от размеров

Размер обуви	35-36	37-38	39-40	41-42	43-44
ni	2	4	9	7	3

1. Составить интервальный статистический ряд распределения частостей наблюдаемых значений непрерывной случайной величины;

2. Построить гистограмму и полигон частостей случайной величины Х;

3. Найти эмпирическую функцию распределения случайной величины и построить ее график;

4. Предполагая, что исследуемая СВ Х распределена по нормальному закону, найти точечные оценки параметров нормального распределения, записать функцию распределения СВ Х;

5. найти теоретические частоты нормального распределения, проверить гипотезу о нормальном законе распределения с помощью критерия согласия 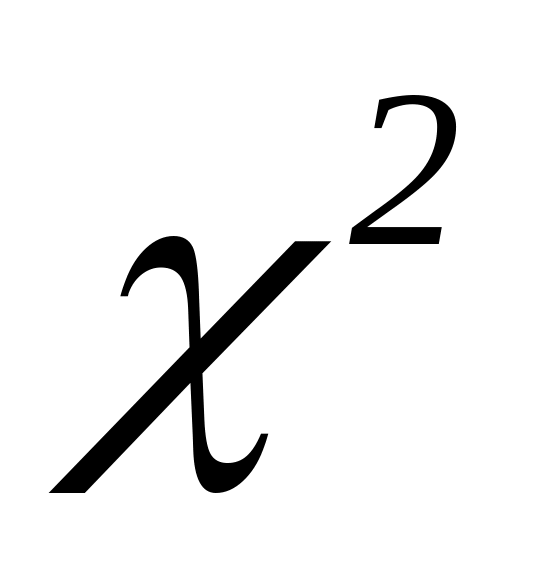- Пирсона (уровень значимости принять равным )

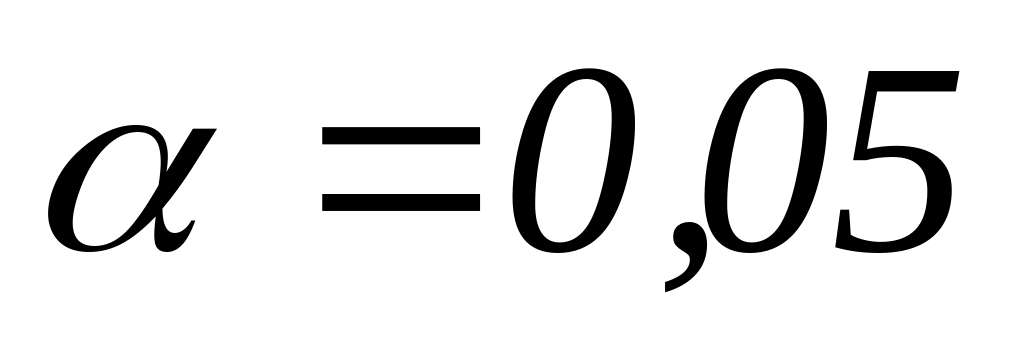6. Найти интервальные оценки параметров нормального распределения (доверительную вероятность принять равной ).

Решение:

1. Найдем статистический ряд частостей, учитывая что частость вычисляется по формуле:

Таким образом, получаем таблицу:

интервал		середина интервала, xi	частота, mi	частость, wi	плотность частости
35	36	35,5	2	0,080	0,00320
37	38	37,5	4	0,160	0,00640
39	40	39,5	9	0,360	0,01440
41	42	41,5	7	0,280	0,01120
43	44	42,5	3	0,120	0,00480
	Σ		25	1,000

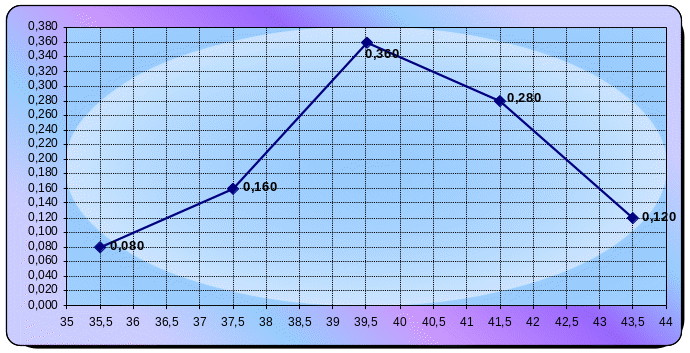
2. Строим гистограмму и полигон частостей случайной величины.

а) Для построения полигона частостей на оси абсцисс откладываем варианты х_i (середины данных интервалов), а на оси ординат - соответствующие им частости; соединив точки (x_i;w_i) получим искомый полигон частостей.

б) Для построения гистограммы частостей, на оси абсцисс откладываем заданные интервалы длины h=6. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся на расстояниях, равных соответствующим плотностям частостей .

3. Найдем эмпирическую функцию распределения СВ и построим ее график.

Для построения эмпирической функции распределения F^* воспользуемся округлением, то есть снова возьмем середины интервалов.

При значениях аргумента, лежащих левее середины первого интервала, то есть при . При значениях х, заключенных в интервале , .

При значениях х, заключенных в интервале ,

При значениях х, заключенных в интервале ,

При значениях х, заключенных в интервале ,

При значениях х, заключенных в интервале ,

Таким образом, получаем значения и график эмпирической функции распределения:

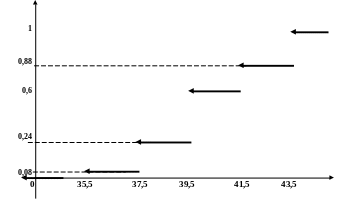
4. Вычислим основные числовые характеристики данного эмпирического распределения:

Для упрощения расчетов составим таблицу:

интервал		середина интервала, xi	частота, mi	ximi	xi^2mi
35	36	35,5	2	71	2520,5
37	38	37,5	4	150	5625
39	40	39,5	9	355,5	14042,25
41	42	41,5	7	290,5	12055,75
43	44	43,5	3	130,5	5676,75
	Σ		25	997,5	39920,25

Таким образом,

выборочная средняя равна:

выборочная дисперсия:

выборочное среднее квадратическое отклонение:

Найдем точечные оценки параметров нормального распределения.

Точечной оценкой математического ожидания является выборочная средняя:

Точечной несмещенной оценкой дисперсии является несмещенная выборочная дисперсия:

тогда

Гипотетическая функция плотности соответствующего нормального распределения имеет вид:

Функция распределения имеет вид:

5. Проверим гипотезу о том, что данные получены из нормально распределенной генеральной совокупности с уровнем значимости =0,05.

Составим расчетную таблицу.

интервал		середина интервала, xi	частота, mi					pi	n'i=npi	mi-n'i	(mi-n'i)^2	(mi-n'i)^2/n'i
35	36	35,5	2		-1,74		-0,459	0,041	1,0225	0,9775	0,95550625	0,93448
37	38	37,5	4	-1,30	-0,85	-0,403	-0,302	0,101	2,5225	1,4775	2,18300625	0,865414
39	40	39,5	9	-0,40	0,04	-0,155	0,160	0,315	7,885	1,115	1,243225	0,15767
41	42	41,5	7	0,49	0,94	0,188	0,326	0,139	3,4625	3,5375	12,51390625	3,614125
43	44	43,5	3	1,39		0,418	0,500	0,082	2,0575	0,9425	0,88830625	0,431741
	Σ		25					0,678	16,95			6,003429

Где 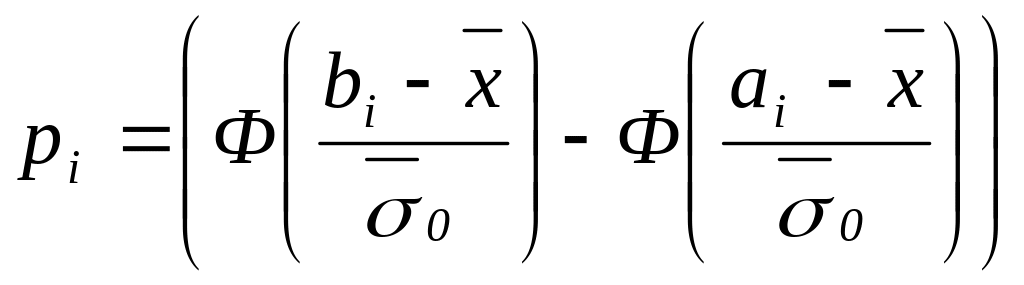. Таким образом .

По таблице критических точек распределения , по уровню значимости и числу степеней свободы находим критическую точку правосторонней критической области .

Так как - гипотезу о нормальном распределении генеральной совокупности отвергаем.

6. Если СВ Х генеральной совокупности распределена нормально, то с надежностью можно утверждать, что математическое ожидание а СВ Х покрывается доверительным интервалом

Где - точность оценки.

Все величины, кроме t известны. Найдем t из соотношения . По таблице значений функции Лапласа находим, t=1,96.

, , n=25.

Таким образом, окончательно получаем доверительный интервал:

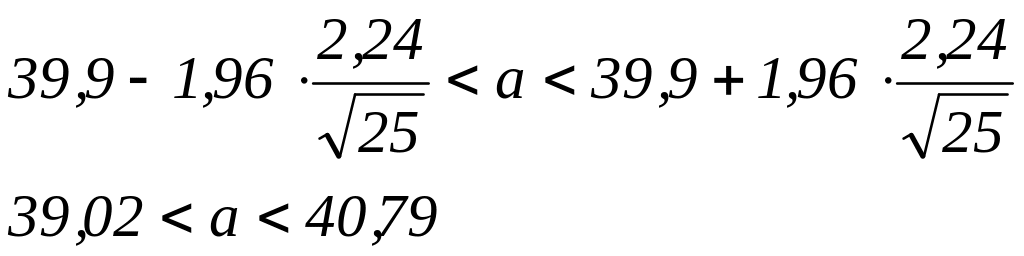
Доверительный интервал для среднего квадратического отклонения имеет вид:

где квантили распределения , с n-1=24 степенями свободы.

Доверительный интервал для среднего квадратического отклонения имеет вид, учитывая что:

Таким образом, доверительный интервал для среднего квадратического отклонения имеет вид:

Задание 10

Приводятся результаты наблюдений (х_i;y_i) над двумерной СВ (Х,У). Используя эти экспериментальные данные, необходимо:

1. построить корреляционное поле. По характеру расположения точек на корреляционном поле подобрать математическую модель регрессионной зависимости У от Х и Х от У (рекомендуется использовать модель линейной регрессии);

2. определить числовые характеристики выборки ;

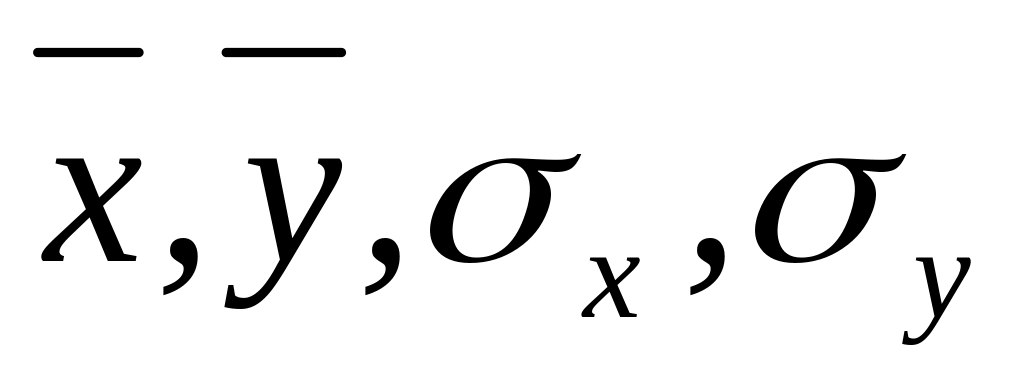3. написать выборочные уравнения прямых линий регрессии у на х и х на у;

4. вычислить коэффициент корреляции и проверить гипотезу о значимости коэффициента линейной корреляции при α=0,05;

	10	20	30	40	nу
20	1				1
40	4	1			5
60	1	15	1		17
80		2	13		15
100			2	1	3
120				9	9
nх	6	18	16	10	50

Решение:

1. Построим корреляционное поле.

По оси абсцисс отложим значения Х, а по оси ординат значения У. Точками покажем сочетания Х и У.

Для всех вычислений, составим таблицу:

			10		20		30	40	nу	nуу	nуу^2
20			1						1	20	400
40			4		1				5	200	8000
60			1		15		1		17	1020	61200
80					2		13		15	1200	96000
100							2	1	3	300	30000
120								9	9	1080	129600
nх			6		18		16	10	50	3820	325200
nхх			60		360		480	400	1300
nхх^2			600		7200		14400	16000	38200
UiVj muv
200	0	0		0
1600	800	0		0
600	18000	1800		0
0	3200	31200		0
0	0	6000		4000
0	0	0		43200
110600

2) Найдем числовые характеристики двумерной св:

Найдем выборочные средние

Найдем выборочные дисперсии

Выборочные среднеквадратические отклонения

3. Найдем уравнение линейной регрессии у на х и х на у.

Уравнение линейной регрессии У на Х ищем в виде .

Ее коэффициенты a и b находим по методу наименьших квадратов из системы уравнений вида:

Так как

то система примет вид:

Таким образом, уравнение линейной регрессии имеет вид:

Найдем уравнение линейной регрессии Х на У. Уравнение линейной регрессии ищем в виде .

Ее коэффициенты с и d находим по методу наименьших квадратов из системы уравнений вида:

Таким образом система принимает вид:

Таким образом, уравнение линейной регрессии имеет вид: