Вопрос 31: Формулы Тейлора для основных элементарных функций (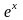 , ln(1+x)).

Рассмотрим несколько важнейших элементарных функций и найдём для них многочлены Тейлора при .

Рассмотрим функцию . Все её производные совпадают с ней: , так что коэффициенты Тейлора в точке равны 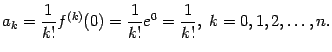Поэтому формула Тейлора для экспоненты такова:

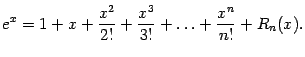
Рассмотрим функцию f(x) = ln(1 + x).

f(x) = ;

………………………………………

Итого:

Полученная формула позволяет находить значения любых логарифмов (не только натуральных) с любой степенью точности. Ниже представлен пример вычисления натурального логарифма ln1,5. Сначала получено точное значение, затем – расчет по полученной выше формуле, ограничившись пятью членами разложения. Точность достигает 0,0003.

ln1,5 = 0,405465108108164381

Вопрос 32: Формулы Тейлора для основных элементарных функций (тригонометрические функции)

Рассмотрим несколько важнейших элементарных функций и найдём для них многочлены Тейлора при .

Рассмотрим функцию . Её производные чередуются в таком порядке: а затем цикл повторяется. Поэтому при подстановке также возникает повторение: и т. д. Все производные с чётными номерами оказываются равными 0; производные с нечётными номерами равны 1 при , то есть при , и при , то есть при . Таким образом, при всех и коэффициенты Тейлора равны Получаем формулу Тейлора для синуса: 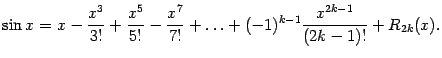Заметим, что мы можем записать остаточный член вместо (как можно было бы подумать), поскольку можно считать, что слагаемое порядка , с коэффициентом, равным 0, тоже включено в многочлен Тейлора.

Для функции производные также чередуются с циклом длины 4, как и для синуса. Значения в точке имеют то же чередование: Нетрудно видеть, что при , и при , . Поэтому разложение косинуса по формуле Тейлора имеет вид Здесь мы также считаем, что последним в многочлене Тейлора выписано слагаемое, содержащее с нулевым коэффициентом.

Вопрос 33: Монотонные функции. Достаточные условия монотонности.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Определения

Пусть дана функция Тогда

функция называется возраста́ющей на , если

.

функция называется стро́го возраста́ющей на , если

.

функция называется убыва́ющей на , если

.

функция называется стро́го убыва́ющей на , если

.

(Строго) возрастающая или убывающая функция называется (строго) монотонной

Достаточные условия монотонности функции на интервале

Теорема: для того чтобы дифференцируемая на интервале (a;b) функция возрастала (убывала) на этом интервале достаточно, чтобы производная была положительной (отрицательной) всюду на этом интервале.

Доказательство. Рассмотрим случай, когда . Пусть x1 и x2 - любые две точки интервала (a;b), удовлетворяющие условию . На отрезке функция дифференцируема, а, следовательно, непрерывна. Поэтому к ней можно применить формулу Лагранжа:

,

где .

По условию . Поэтому или , т.е. функция возрастает на интервале (a;b). Случай, когда , рассматривается аналогично.

Теорема доказана.

Вопрос 34: Локальные экстремумы. Исследование функции на экстремум. Необходимые, достаточные условия экстремума.

Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Определения

Пусть дана функция и — внутренняя точка области определения Тогда

называется точкой локального максимума функции если существует проколотая окрестность такая, что

называется точкой локального минимума функции если существует проколотая окрестность такая, что

Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.

называется точкой абсолютного (глобального) максимума, если

называется точкой абсолютного минимума, если

Значение функции называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума

Замечание: Функция определённая на множестве может не иметь на нём ни одного локального или абсолютного экстремума. Например,

Необходимые условия существования локальных экстремумов

Из леммы Ферма вытекает следующее:

Пусть точка является точкой экстремума функции , определенной в некоторой окрестности точки .

Тогда либо производная не существует, либо .

Достаточные условия существования локальных экстремумов

Пусть функция непрерывна в и существуют конечные или бесконечные односторонние производные . Тогда при условии

является точкой строгого локального максимума. А если

то является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке

Пусть функция непрерывна и дважды дифференцируема в точке . Тогда при условии

и

является точкой локального максимума. А если

и

то является точкой локального минимума.

План исследования функции на экстремум:

-Найти область определения функции.

-Найти производную.

-Найти критические точки, в которых производная равна нулю или не существует. Расположить их в порядке возрастания.

-Исследовать знак производной в полученных промежутках.

-Вычислить значение функции в точках максимума и минимума.

Достаточные признаки возрастания и убывания функции.

На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:

-если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

-если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

-найти область определения функции;

-найти производную функции;

-решить неравенства и на области определения;

-к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Достаточные признаки экстремума функции.

Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума. Хотя самым распространенным и удобным является первый из них. Первое достаточное условие экстремума. Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда

если при и при , то - точка максимума;

если при и при , то - точка минимума.

Другими словами: если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то - точка максимума;

если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума.

Алгоритм.

-Находим область определения функции.

-Находим производную функции на области определения.

-Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (эти точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).

-Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).

-Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак.