Плотность энергетических состояний и распределение электронов по энергиям
Состояние частиц обычно определяют в
фазовом пространстве (пространстве
импульсов и координат). Электрон, как и
другие квантовые частицы с полуцелым
спином, подчиняется принципу
неопределенности. Это означает, что
разным элементам фазового объема будут
отвечать различные квантовые состояния
лишь в том случае, если объем этих
элементов не меньше
,
то есть за элементарную ячейку фазового
пространства следует принять объем
.
Считая потенциальную энергию одинаковой
во всех точках физического объема, можно
перейти от фазового пространства к
пространству импульсов (или
-
пространству), в котором элементарная
ячейка имеет объем
где
– объем кристалла.
Определим плотность энергетических
состояний
,
то есть число состояний в единичном
интервале энергий для единичного объема
кристалла
(4.70)
Вид функции зависит от того, как сама энергия выражается через квазиимпульсы частиц. Если в пространстве квазиимпульсов (или -пространстве) через точки с одинаковыми значениями энергии провести поверхность, то получим так называемую изоэнергетическую поверхность.
В приближении свободных электронов энергия определяется выражением
(4.71)
где – энергия, соответствующая дну зоны проводимости. Изоэнергетическими поверхностями в этом случае являются сферы (рис.4.16).
Объем шарового слоя между сферами
радиусов
и
равняется
.
В нем может разместиться элементарных
ячеек (с учетом спина электрона)
а в единичном объеме кристалла
(4.72)
-
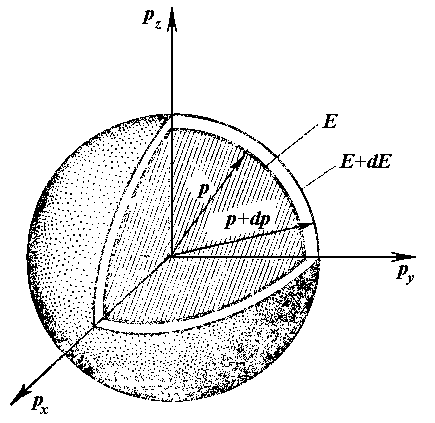
Рис.4.16. Изоэнергетические поверхности в пространстве квазиимпульсов
Выражая
и
из (4.71) и подставляя в (4.72), получаем для
плотности состояний в зоне проводимости
(4.73)
Для состояний вблизи потолка зоны энергия имеет вид
(4.74)
и плотность состояний определяется выражением
(4.75)
Умножив (4.73) на вероятность заполнения
данного энергетического состояния
электроном, то есть на функцию Ферми-Дирака
получим распределение электронов по
энергиям (принимаем
)
(4.76)
С математической точки зрения
есть функция, которая зависит от двух
параметров
и
:
(4.77)
Здесь
есть постоянная Больцмана.
При данной величине энергии Ферми
функция представляет собой семейство
кривых, зависящих от температуры
(рис.4.17, а). При
функция
терпит разрыв в точке
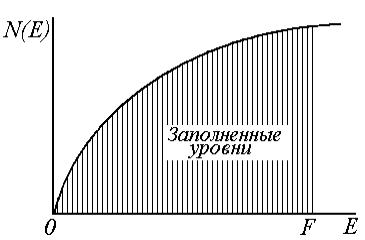
График распределения электронов по
энергиям представлен на рис. 4.17 б.
При абсолютном нуле состояния в зоне
проводимости заполнены вплоть до уровня
Ферми, состояния выше энергии Ферми –
свободные. При
часть электронов за счет термического
возбуждения переходит на свободные
уровни, лежащие выше уровня Ферми.
|
|
а |
б |
Рис.4.17. Вид функции Ферми при различных температурах (а) и распределение электронов по энергиям (б) |
|
