§ 9.3. Затухающие колебания

Опыт показывает, что свободные колебания реальных физических систем затухают, так как первоначальный запас энергии колебаний расходуется на преодоление сопротивления и превращается в теплоту, излучение и т.д. Количественной характеристикой затухания служит добротность колебательной системы - Q, равная отношению энергии колебаний W к ее потерям W²³:

Q=W/W (9.3.1)

Из определения следует, чем больше добротность, тем медленнее затухают колебания, и тем ближе колебательная система к идеальной. Добротность гармонического осциллятора равна бесконечности.

Рассмотрим свободные колебания пружинного маятника и учтем тормозящее действие на него окружающей среды (например, воздуха). Помимо возвращающей силы F_возвр=-kx действует сила вязкого трения F_тр=-r, где r - постоянный коэффициент, зависящий от размеров и формы тела, а также от вязкости среды,  - скорость тела.. Запишем уравнение движения : md²x/dt²=-kx-r. Учитывая, что =dx/dt, и введя новые обозначения постоянных коэффициентов 2 =r/m и ₀²=k/m. (их физический смысл выясним чуть позже), получаем линейное дифференциальное уравнение второго порядка с постоянными коэффициентами и без правой части:

d²x/dt²+2dx/dt+₀²x=0. (9.3.2)

Из математики известно, что его решение имеет вид;

x=C₁ exp(₁t)+C₂ exp(₂t), (9.3.3)

где С₁ и C₂ - постоянные, ₁ и ₂ - корни характеристического уравнения ²+2+₀²=0, равные _1,2=-  .

Проанализируем физический смысл полученного результата. Если силы трения малы, т.е.

 ²-₀² <0, то закон движения (1.3.3) удобно записать в виде:

x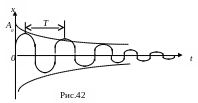 =A₀ exp(- t)sin( t+₀), (9.3.4)

где A₀ и ₀ - постоянные, определяемые начальными условиями, т.е. начальным смещением - x₀ и начальной скоростью - υ₀ при t=0. На рис.42 этот закон движения представлен графиком. Это колебание не является гармоническим, так как размах колебаний уменьшается, поэтому понятия “частота”, “период”, “амплитуда” к нему можно применять условно. Промежуток времени между двумя последовательными максимальными отклонениями маятника от положения равновесия в одну и ту же сторону называют периодом колебаний Т. Циклическая частота

 =(₀² -  ²)^1/2 (9.3.5)

Она тем меньше, а период колебаний T=2/ тем больше, чем больше . Коэффициент перед синусом в законе движения называют амплитудой затухающих колебаний:

A=A₀ e^{-  t} (9.3.6)

На графике она изображена тонкой линией, огибающей максимальные смещения маятника от положения равновесия. Чем больше коэффициент , т.е чем больше трение, тем быстрее затухают колебания. Коэффициент  называют коэффициентом затухания. Обратите внимание, что  t- есть показатель степени, безразмерная величина, так что коэффициент затухания измеряют в СИ в с^-1. Таким образом, трение тормозит движение колебательной системы, увеличивая период колебаний и уменьшая их размах. В идеальной колебательной системе без трения (=0) частота свободных колебаний =₀ и определяется только свойствами самой колебательной системы (упругостью и массой маятника), поэтому ₀ называется собственной циклической частотой.

В качестве количественной характеристики скорости затухания колебаний используют декремент затухания, равный отношению амплитуд двух следующих друг за другом колебаний: A(t)/A(t+T). Логарифм этого отношения называют логарифмическим декрементом затухания:

=lnA(t)/A(t+T)=T (9.3.7)

Выясним его физический смысл. Промежуток времени , в течение которого амплитуда уменьшается в е=2,7 раз, называют временем жизни (или временем релаксации) колебаний. Из формулы (9.3.6) следует, что

=1/ (9.3.8)

За время  система совершает N_е колебаний. Используя (9.3.7) и (9.3.8), получим:

N_e=/T=/=1/ (9.3.9)

Таким образом, логарифмический декремент затухания равен обратному числу колебаний, уменьшающему амплитуду в е раз. Естественно, что логарифмический декремент затухания связан с добротностью Q:

Q=/=N_e (9.3.10)

Если силы трения велики (т.е.  ²-₀² 0), то при ₀, как следует из формулы (9.3.5),   , следовательно,  . Это означает, что система, будучи выведена из положения равновесия, плавно возвращается к нему. Такой процесс называется апериодическим (т.е. непериодическим). Попробуйте самостоятельно нарисовать два примера апериодических законов движения: мысленно поместите пружинный маятник в очень вязкую среду, отклоните его от положения равновесия и толкните его в первом примере к положению равновесия, а во втором примере в противоположную сторону. Как разные начальные условия отразятся на этих графиках?

Свободные колебания часто встречаются в технике. Если колебания должны поддерживаться длительное время, то затухание вредно и с ним нужно бороться, уменьшая трение. В таких случаях в механических устройствах применяют смазку, подшипники и т.п. Например, в механических часах опоры осей делают конической формы из твердых камней (агат, рубин). Если колебания нежелательны, их стремятся погасить, увеличивая трение с помощью успокоителей (демпферов). Подобные устройства используются в звеньях механических машин, гидравлических устройствах, электроизмерительных приборах.

Нередко к наличию колебаний следует подходить диалектически. Гасить их чрезмерной жесткостью опасно, так как это приводит к ударам, разрушающим здания, перевозимые грузы, станки, стрелки измерительных приборов. Подобные удары амортизируют упругими подвесками, растяжками: сейсмическую стойкость зданий обеспечивают мощной упругой “подушкой“; столы для чувствительных измерений, кузова автомобилей, перевозимые хрупкие предметы крепят на упругих подвесках.

Подведем итоги:

1.Уравнение движения свободных механических колебаний в присутствии сил вязкого трения имеет вид: d²x/dt²+2 dx/dt+₀²x=0, где  - коэффициент затухания,₀ - собственная циклическая частота.

2.Характер закона движения определяется величиной трения. Если трение мало (математически это выражается так:  <<₀), то колебания похожи на гармонические, однако их амплитуда экспоненциально уменьшается со временем; и такие колебания называются затухающими. Быстрота затухания (диссипации энергии) характеризуется логарифмическим декрементом затухания, временем жизни колебаний, добротностью колебательной системы. Эти характеристики взаимосвязаны между собой. Если трение велико ( ₀ ), то движение становится апериодическим.

3.Закономерности свободных колебаний, установленные нами для механического движения, справедливы для колебаний любой физической природы, в частности, для электромагнитных колебаний в электрическом колебательном контуре, имеющем сопротивление.