8.5. Спектральное описание циклических кодов.

Рассмотрим еще один способ описания циклических кодов, основанный на использовании дискретного преобразования Фурье (ДПФ) кодовых последовательностей, заданных над конечным полем . Данный подход позволяет в ряде случаев найти альтернативные методы кодирования и декодирования циклических кодов.

В поле комплексных чисел ДПФ вектора с комплексными компонентами определяется как вектор, компоненты которого вычисляются согласно соотношению

.

Ядром преобразования Фурье является , которое является корнемn–й степени из единицы в поле комплексных чисел. В конечном полеэлементпорядкатакже является корнемn–й степени из единицы. Тогда, проводя аналогию междуи, можно ввести следующее определение.

Пусть – вектор над, гдеnделитпри некоторомmи пусть– элемент мультипликативного порядкаnв расширенном поле. Тогда ДПФ над полемвектораявляется векторс элементами, задаваемыми равенствами

,

или в векторном представлении

.

Учитывая ранее указанную аналогию, дискретный индекс iестественно назватьдискретным временем, а вектор–временной функцией(последовательностью) илисигналом. Аналогично, индексkможно назватьдискретной частотой, а вектор–частотной функцией(последовательностью) илиспектром.

Если спектр определяется прямым ДПФ, то с помощью обратного ДПФ по спектру может быть определен сам сигнал, т.е. компоненты вектора

.

Следует также отметить, что если ДПФ вещественнозначной временной функцииявляется комплексным, то аналогично при преобразовании в поле Галуа временной функции, элементы которой принадлежат полю, ее спектрлежит в расширенном поле.

Преобразование Фурье обладает рядом замечательных свойств, которые переносятся и на случай преобразования в конечных полях.

Теорема 8.5.1 (Теорема о свертке).Пусть– временные последовательности, причем. Тогда компоненты ДПФмогут быть определены как

где двойные скобки означают, что индекс вычисляется в арифметике по модулю n.

Доказательство:Вычислим преобразование Фурье векторас компонентами вида

.

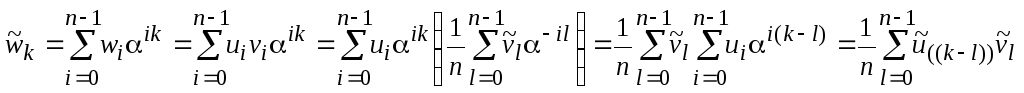Можно сформулировать и обратную теорему, поменяв местами временную и частотную области.

Теорема 8.5.2.Пусть– частотные последовательности, причем. Тогда компоненты векторамогут быть определены как

где двойные скобки означают, что индекс вычисляется в арифметике по модулю n.

Отметим также, что выбор в теореме о свертке приводит к формуле типа равенства Парсеваля

.

Замечание.Основываясь на этом свойстве ДПФ, возможен альтернативный вариант описания циклических кодов. Любое кодовое слово циклического кода может быть представлено в несистематическом виде как

,

где – информационный, а– проверочный полиномы. Во временной области коэффициенты кодового полинома определяются циклической сверткой коэффициентов информационного и порождающего полиномов

,

так что в частотной области, согласно теореме 8.5.2, операция кодирования может быть осуществлена покомпонентным перемножением спектров

и последующим вычислением обратного ДПФ для спектра кодового слова.

Теорема 8.5.3 (Свойство сдвига).Если последовательностииявляются парой преобразования Фурье, то парами преобразований Фурье являются такжеи.

Доказательствоосуществляется непосредственной подстановкой.

В том случае, когда кодовому вектору сопоставляется полином, он может быть преобразован в полином, коэффициенты которого отвечают спектральным компонентам ДПФ в поле Галуа вектора, а сам полином называетсяспектральным(илиассоциированным) смногочленом. Следующая теорема устанавливает, что свойства спектра тесно связана с корнями многочленов.

Теорема 8.5.4.

(i). Элементявляется корнем полиноматогда и только тогда, когдаk–й частотный компонентравен нулю.

(ii). Элементявляется корнем многочленатогда и только тогда, когдаi–й временной компонентравен нулю.

Доказательствоутверждения (i) очевидно, поскольку из непосредственной подстановки корня в полиномимеем

.

Аналогичным образом доказывается и утверждение (ii).

На основании приведенной теоремы можно сделать следующее заключение. Поскольку любой кодовый многочлен содержит в качестве множителя порождающий многочлен, то корни порождающего полинома являются и корнями кодового. Тогда, согласно теореме 8.5.4, корням порождающего многочлена будут соответствовать нулевые спектральные компоненты кодовых слов на позициях. Следовательно, можно дать следующее альтернативное определение циклического кода. Циклическим кодомназывается множество таких слов над конечным полем, у которых все спектральные компоненты, принадлежащие заданному множеству т.н. проверочных частотравны нулю.

Пример 8.5.1.Для (7,4) циклического кода, задаваемого порождающим многочленом, построить все кодовые словаи их спектры.

Из примеров 7.4.1 и 7.7.1 следует, что порождающая и проверочнаяматрицы данного кода определены как

и.

Отметим (см. таблицу 8.2 из примера 8.2.5), что столбцами проверочной матрицы являются двоичные эквиваленты последовательных степеней примитивного элементаполя, т.е..

Результаты построения циклического кода во временной и частотной областях сведены в таблицу 8.4. Заполнение таблицы 8.4 иллюстрирует пример для конкретного информационного вектора. Пусть , тогда кодовое слово в систематическом виде может быть получено как

В свою очередь спектр данного кодового слова может быть определен на основе непосредственного вычисления ДПФ в матричной форме

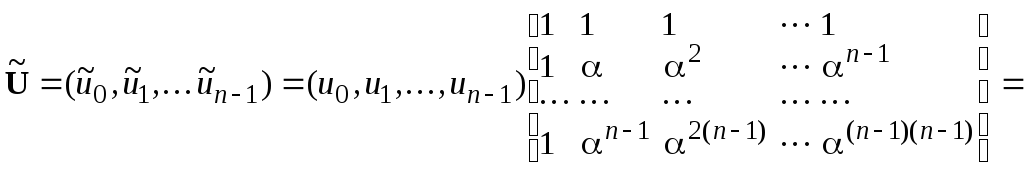
где учтены как порядок примитивного элемента , так и правила сложения элементов поля.

Как следует из таблицы, особенность спектров всех кодовых слов данного циклического кода состоит в том, что спектральные компоненты . Последний факт не должен вызывать особого удивления, поскольку корнями порождающего полинома, а значит и корнями кодовых полиномов, являются сам примитивный элементи его степени. Тогда, согласно теореме 8.5.4, спектральные компоненты, и именно они образуют т.н. проверочное множество частот.

Таблица 8.4.

Кодовые слова во временной области							Спектр кодовых слов.
u0	u1	u2	u3	u4	u5	u6
0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	1	0	1	0	0	0	1	0	0		0
0	1	1	0	1	0	0	1	0	0	1	0	1	1
1	0	1	1	1	0	0	0	0	0		0
1	1	1	0	0	1	0	0	0	0		0
0	0	1	1	0	1	0	1	0	0		0
1	0	0	0	1	1	0	1	0	0		0
0	1	0	1	1	1	0	0	0	0		0
1	0	1	0	0	0	1	1	0	0		0
0	1	1	1	0	0	1	0	0	0		0
1	1	0	0	1	0	1	0	0	0		0
0	0	0	1	1	0	1	1	0	0		0
0	1	0	0	0	1	1	1	0	0		0
1	0	0	1	0	1	1	0	0	0	1	0	1	1
0	0	1	0	1	1	1	0	0	0		0
1	1	1	1	1	1	1	0	0	0	0	0	0	0