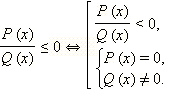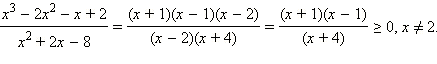3.2. Решение неравенств
|
|
|
|
Пусть функции f (x) и g (x) заданы на некоторых числовых множествах X1 и X2. Неравенством с одной неизвестной называется отношение вида
|
f (x) < g (x). |
(1) |
(Вместо знака < могут стоять знаки >, ≤, ≥.)
Областью
допустимых значений неравенства
(ОДЗ) называется множество значений
переменной, на котором обе части
неравенства одновременно определены
(имеют смысл). Таким образом,
![]() то
есть пересечение множеств
то
есть пересечение множеств
![]() и
и
![]()
Число a называется решением неравенства (1), если при подстановке его вместо переменной x получаем верное числовое неравенство f (a) < g (a).
Понятно, что a, являясь решением неравенства (1), может лежать только в ОДЗ.
Поскольку проверить решение в неравенствах не так просто, как в уравнениях, искать решения лучше сразу в ОДЗ.
Решить неравенство − это означает найти все его решения или доказать, что их нет. Совокупность всех решений неравенства называется множеством решений неравенства.
Два неравенства,
|
f (x) < g (x) |
(2) |
и |
|
f1 (x) < g1 (x), |
(3) |
называются равносильными на множестве X, если на этом множестве неравенства имеют одни и те же решения, то есть, если каждое решение неравенства (2) является решением неравенства (3), и наоборот, каждое решение второго неравенства является решением первого. Два неравенства, не имеющие решений на каком-либо множестве, также считаются равносильными на этом множестве.
Из приведённого определения следует, что если неравенство f1 (x) < g1 (x) окажется более простым, чем равносильное ему неравенство f (x) < g (x), то и решать нужно именно его, так как решения у него те же. Остаётся единственная проблема: как от неравенства (2) перейти к равносильному ему неравенству (3) или, как говорят, осуществить равносильный переход? Сформулируем несколько общих правил, позволяющих это делать.
Правило 1. Если функции f (x), g (x) и h (x) определены на множестве X, то неравенства
f (x) > g (x) и f (x) + h (x) > g (x) + h (x) |
равносильны на этом множестве.
Правило 2. Если h (x) > 0 на множестве X, то неравенства
|
равносильны на этом множестве.
Вывод. Обе части неравенства можно умножать на положительную функцию, не нарушая равносильности.
Правило 3. Если h (x) < 0 на множестве X, то неравенства
|
равносильны на этом множестве.
Вывод. Обе части неравенства можно умножать на отрицательную функцию, не нарушая равносильности, меняя при этом знак неравенства на противоположный.
Правило 4. Если f (x) ≥ 0, g (x) ≥ 0 на множестве X, то неравенства
|
равносильны на этом множестве.
Вывод.
Если обе части неравенства
![]() неотрицательны,
то возведение в квадрат неравенства не
нарушает равносильности. Заметим, что
возводить неравенство в квадрат можно,
только если обе части этого неравенства
неотрицательны. Если хотя бы одна из
частей неравенства отрицательна,
возведение неравенства в квадрат, вообще
говоря, не является равносильным
преобразованием. Яснее всего это видно
на примере числовых неравенств. Так,
если верное неравенство −1 > −4
возвести в квадрат, то получится неверное
неравенство 1 > 16. Такое противоречие
вызвано именно тем, что части первоначального
неравенства не были неотрицательными.
неотрицательны,
то возведение в квадрат неравенства не
нарушает равносильности. Заметим, что
возводить неравенство в квадрат можно,
только если обе части этого неравенства
неотрицательны. Если хотя бы одна из
частей неравенства отрицательна,
возведение неравенства в квадрат, вообще
говоря, не является равносильным
преобразованием. Яснее всего это видно
на примере числовых неравенств. Так,
если верное неравенство −1 > −4
возвести в квадрат, то получится неверное
неравенство 1 > 16. Такое противоречие
вызвано именно тем, что части первоначального
неравенства не были неотрицательными.
Пример 1
Равносильны
ли неравенства
![]()
Решение
Неравенства неравносильны. Действительно,
Неравенство x + 3 < 5 будет верным и тогда, когда x + 3 < –5, например, при x = –100. Первое же неравенство при x = –100 неверно. Ответ. Нет. |
Пример 2
Равносильны
ли неравенства
![]() и
и
![]()
Решение
Неравенства неравносильны. В самом деле,
Значит, множеством решений первого неравенства являются область x ≥ 0, а второго x > –1. Поскольку это разные множества, то неравенства неравносильны. Ответ. Нет. |
3.2.2. Рациональные неравенства
Рассмотрим выражение вида:
|
|
(1) |
(Вместо знака < могут стоять знаки >, ≤, ≥.)
Основным методом решения неравенств вида (1) является метод интервалов. Начнём рассматривать его, прежде всего, для многочленов. Этот метод основан на том, что двучлен (x – a) положителен при x > a и отрицателен при x < a, то есть при переходе через точку x = a этот двучлен меняет знак.
Отсюда следуют полезные замечания.
Многочлен
 то
есть двучлен в нечётной степени,
положителен и отрицателен на тех же
интервалах, что и (x – a).
то
есть двучлен в нечётной степени,
положителен и отрицателен на тех же
интервалах, что и (x – a).Многочлен
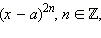 то
есть двучлен в чётной степени, не меняет
знак при переходе через точку x = a,
а в самой точке обращается в нуль.
то
есть двучлен в чётной степени, не меняет
знак при переходе через точку x = a,
а в самой точке обращается в нуль.
Вывод.
Многочлены вида
при
решении строгих неравенств («<» или
«>») можно опустить, так как они не
влияют на знак неравенства. При этом из
решения нужно исключить точки, в которых
многочлен равен нулю:![]()
Многочлен
 всегда
положителен и потому при решении любого
неравенства может быть опущен.
всегда
положителен и потому при решении любого
неравенства может быть опущен.При переходе через точку x = a может изменить знак только двучлен (x – a), остальные двучлены не меняют знака.
Пример 1
Решите неравенство
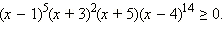
Решение
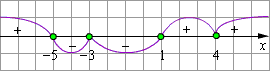
Отметим на числовой оси нули многочлена, стоящего в левой части неравенства. При x > 4 все множители положительны. При переходе через точку x = 4 многочлен не меняет знак, так как двучлен (x – 4) входит в чётной степени. При переходе через точку x = 1 знак многочлена изменится, так как (x – 1) входит в нечётной степени. На промежутке (–5; –3) многочлен отрицателен, так как при переходе через точку x = –3 он не изменит знак (множитель (x + 3) в чётной степени). При переходе через точку x = –5 знак опять меняется, так как (x + 5) входит в первой степени.
Чередование знаков отразим на рисунке с помощью так называемой кривой знаков. Наиболее быстро это можно сделать следующим образом. Выясним, какой знак имеет многочлен на самом правом промежутке, для этого нужно лишь понять, какие знаки будут иметь все сомножители, если в этот многочлен подставить достаточно большое число (большее самого большого корня многочлена). После этого определяем знак всего многочлена на этом промежутке и начинаем рисовать кривую знаков справа налево, переходя через точки (меняя знак) или «отражаясь» от числовой оси (если степень двучлена, соответствующего данной точке, чётна). Теперь, двигаясь в обратном направлении, с рисунка считываем:
Ответ. |
Если правая и левая части данного неравенства являются дробно-рациональными функциями, то это неравенство называется рациональным.
Рассмотрим стандартный приём решения рациональных неравенств, основанный на сведении данного неравенства к неравенству для многочлена, метод решения которого (метод интервалов) нам уже известен. Итак, рассмотрим рациональное неравенство
f (x) > g (x), |
где
f (x) и g (x) − рациональные функции,
то есть функции, представимые в виде
отношения многочленов. Перенося обе
части рационального неравенства в левую
часть, представим её в виде отношения
двух многочленов:
 (Такой
вид неравенства называется стандартным.)
Заметим, что:
(Такой
вид неравенства называется стандартным.)
Заметим, что:
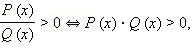 то
есть отношение двух многочленов
положительно тогда и только тогда,
когда положительно их произведение.
то
есть отношение двух многочленов
положительно тогда и только тогда,
когда положительно их произведение.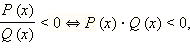 то
есть отношение двух многочленов
отрицательно тогда и только тогда,
когда отрицательно их произведение.
то
есть отношение двух многочленов
отрицательно тогда и только тогда,
когда отрицательно их произведение.
Итак,
|
|
Левая
часть полученных неравенств есть
произведение многочленов, то есть сама
является многочленом. А поскольку его
знак совпадает со знаком дроби
![]() то
дробь меняет или не меняет знак при
переходе через точку x = a в зависимости
от того, входит в него двучлен (x – a)
в чётной или нечётной степени.
то
дробь меняет или не меняет знак при
переходе через точку x = a в зависимости
от того, входит в него двучлен (x – a)
в чётной или нечётной степени.
Если
же двучлен (x – a) входит в многочлен
P (x) в степени k, а в многочлен Q (x) −
в степени l, то в многочлен P (x) · Q (x)
этот двучлен войдёт в степени k + l,
а в дробь
![]() −
в степени k – l. Легко проверить,
что для любых чисел k и l чётность чисел
k + l и k – l одинакова.
Следовательно, вывод о поведении дроби
при
переходе через точку x = a мы сделаем
в точности такой же, как если бы наше
неравенство было представлено в виде
многочлена P (x) · Q (x).
−
в степени k – l. Легко проверить,
что для любых чисел k и l чётность чисел
k + l и k – l одинакова.
Следовательно, вывод о поведении дроби
при
переходе через точку x = a мы сделаем
в точности такой же, как если бы наше
неравенство было представлено в виде
многочлена P (x) · Q (x).
Таким образом, показан принципиальный метод решения рациональных неравенств. Имея в виду последнее замечание, метод интервалов для рациональных функций можно сформулировать в следующем виде.
Привести неравенство к стандартному виду
Разложить на множители многочлены P (x) и Q (x) (как мы знаем, для этого придётся решить уравнения P (x) = 0 и Q (x) = 0).
Нули числителя, не совпадающие с нулями знаменателя, отметить на числовой оси точками, а нули знаменателя − кружочками (эти точки, очевидно, не входят в ОДЗ рациональной функции и потому они как будто «выколоты» из числовой оси).
Подставить мысленно в неравенство очень большое число (большее самого большого из корней числителя и знаменателя) для того, чтобы определить, какой знак имеет рациональная функция на самом правом интервале. Провести кривую знаков, проходя через все точки, отмеченные на числовой прямой, меняя или не меняя знак в зависимости от суммарной степени двучлена, отвечающего данной точке.
Записать ответ, обращая особое внимание на граничные точки, часть из которых может быть «выколота».
Таким образом, для нестрогих рациональных неравенств имеем по определению
|
Пример 2
Решить
неравенство
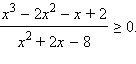
Решение
Имеем
Наносим на числовую ось нули числителя и знаменателя и, строя кривую знаков, по указанному алгоритму сразу получаем:
Ответ. |
Заметим, что на двучлен (x – 2) можно спокойно сокращать; встретившись и в числителе и в знаменателе, он не будет влиять на знак неравенства. Надо лишь не забыть, что x ≠ 2, так как при x = 2 не определён знаменатель данной дроби.