10. Уравнение Шредингера для гармонического осциллятора

Гармонический осциллятор представляет собой частицу массой m, совершаю-

щую одномерное колебательное движение под действием квазиупругой силы . Ее потенциальная энергия имеет вид

,

где . Уравнение Шредингера для гармонического осциллятора:

.

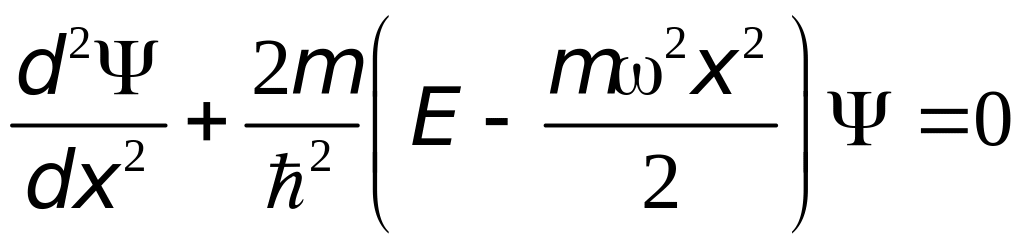В теории дифференциальных уравнений показывается, что это уравнение имеет конечные, однозначные и непрерывные решения при значениях энергии

, .

Энергетические уровни являются эвидистантными, т. е. находящимися на одинаковом расстоянии друг от друга и с точностью до слагаемого совпадают с формулой Планка для квантов энергии излучения АЧТ . При - энергия нулевых колебаний - наименьшая энергия, которой должен обладать линейный гармонический осциллятор в основном энергетическом состоянии. Таким образом, энергия гармонического осциллятора в принципе не может обращаться в нуль. Существование энергии нулевых колебаний является прямым следствием соотношения неопределенностей Гейзенберга, которое в наиболее общем виде можно представить в виде:

,

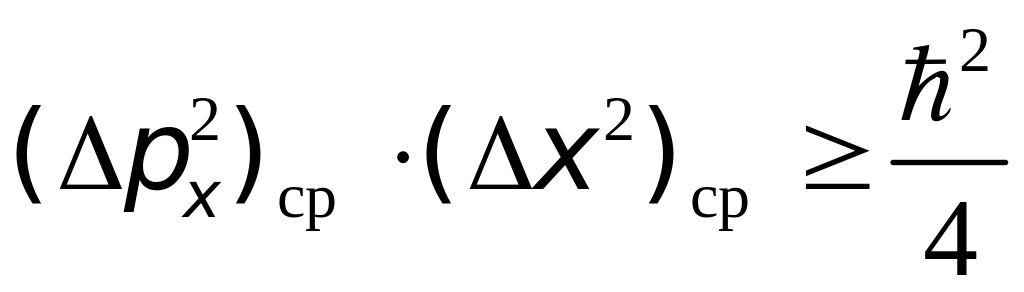где - среднеквадратичное отклонение для импульса от его среднего значения, - среднеквадратичное отклонение для координаты. Можно показать, что для осциллятора , а , поэтому соотношение неопределенностей перепишется в виде:

Тогда для энергии осциллятора получим .

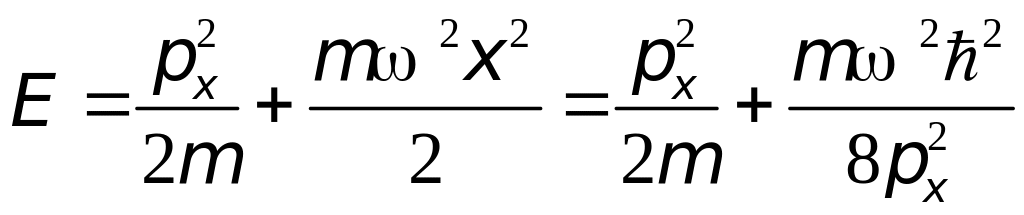Дифференцируя это выражение по p² и приравнивания результат к нулю (условие

минимума), найдем . Отсюда, . Если бы энергия частицы равнялась нулю, то равнялись бы нулю ее координаты и импульс, т.е. и .

Соотношение неопределенностей, как мы видели выше, позволяет оценить минимальную энергию гармонического осциллятора.

Схема энергетических уровней квантового осциллятора, соответствующие им собственные волновые функции (сплошные линии) и плотности вероятностей (пунктирные линии) представлены на Рис. 18. Как видно из рисунка, для каждого уровня E_n существует отличная от нуля вероятность нахождения микрочастицы за пределами потенциального барьера в классически недоступной области E < U(x), где .

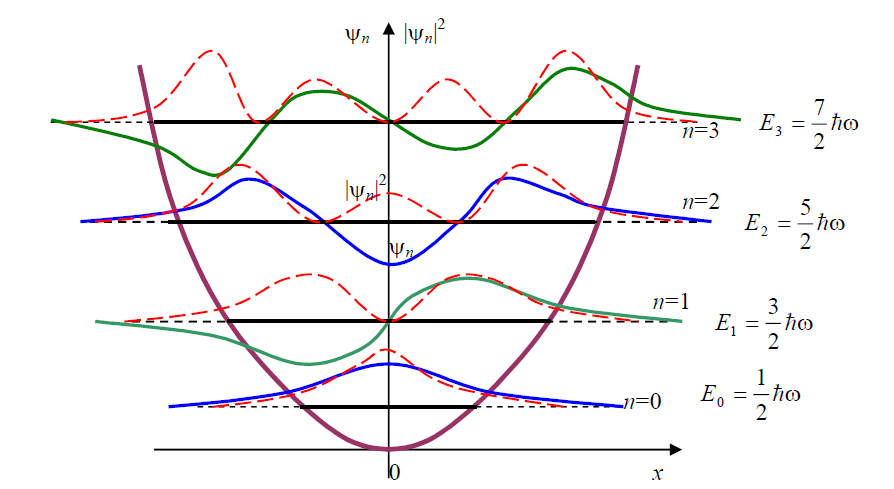
Рис.18 Схема энергетических уровней квантового осциллятора

III. Основы атомной физики

11. Уравнение Шредингера для атома водорода

Уравнение Шредингера для движения электрона в атоме водорода записывается в виде

,

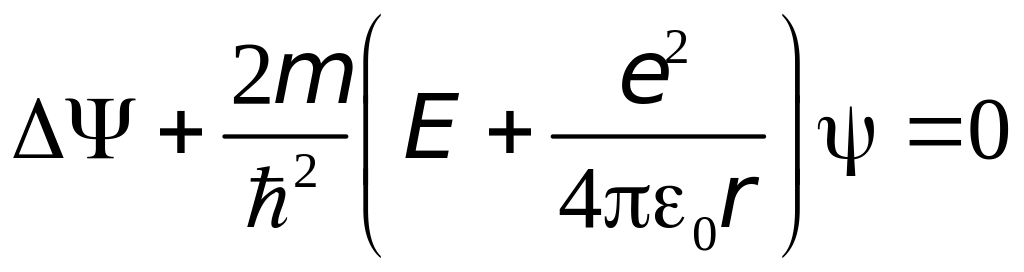где 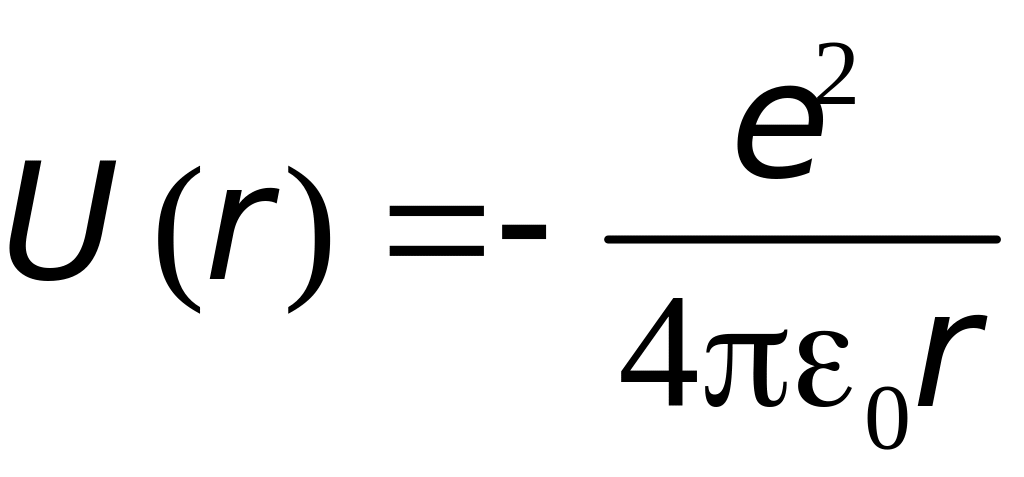- функция, соответствующая потенциальной энергии взаимодействия электрона с ядром, - расстояние между электроном и ядром, e – заряд электрона. Уравнение удобнее записать в сферической системе координат :

.

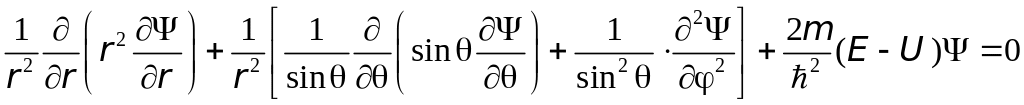Это уравнение имеет решение при значениях энергии электрона в атоме водорода:

,

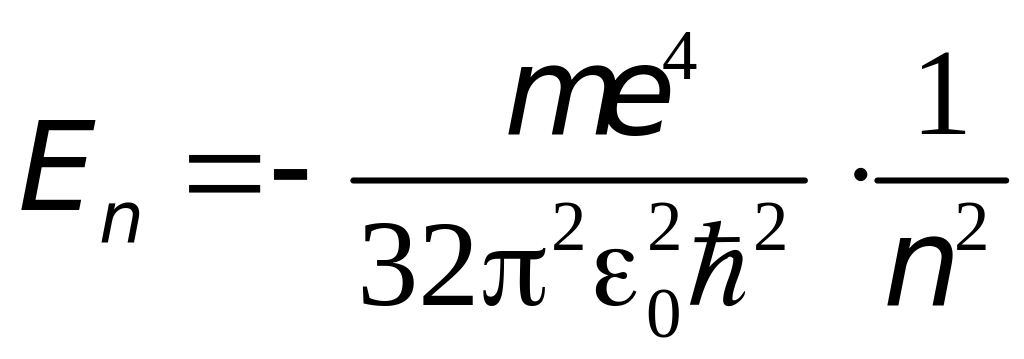где –главное квантовое число. Собственные функции этого уравнения Шредингера можно представить в виде произведения двух функций

,

где - радиальная часть волновой функции, зависящая только от , задается квантовыми числами и , а - угловая часть волновой функции задается квантовыми числами и , определяющими момент импульса электрона.

12. Квантование момента импульса. Квантовые числа. Орбитальный магнитный момент электрона

В квантовой механики невозможно полностью задать вектор момента импульса L, т.е. определить его проекции на оси координат. Возможно лишь определение модуля вектора и его проекции на одну из осей (обычно ось z). Модуль орбитального момента импульса принимает значения:

,

где – орбитальное квантовое число, ( ). Проекция вектора орбитального момента импульса на заданное направление (ось ):

,

где –магнитное квантовое число, ( ).

Собственные волновые функции уравнения Шредингера для движения электрона в атоме водорода зависят от трех квантовых чисел, имеющих следующий смысл:

Главное квантовое число определяет уровни энергии электрона в атоме водорода.

Орбитальное квантовое число , которое при данном может принимать значения , задает модуль орбитального момента импульса электрона относительно ядра.

Магнитное квантовое число , которое при данном принимает зна-

чений , определяет проекции орбитального момента импульса элек

трона на некоторое произвольно выбранное направление .

С механическим моментом электрона связан магнитный момент . Отношение магнитного момента к механическому называется гиромагнитным отношением. В классической физике магнитный момент электрона в атоме равен

,

а механический момент , где e, m_e - заряд и масса электрона, –скорость, r - радиус его орбиты. Переходя к обозначениям атомной физики , для гиромагнитного отношения получим ,

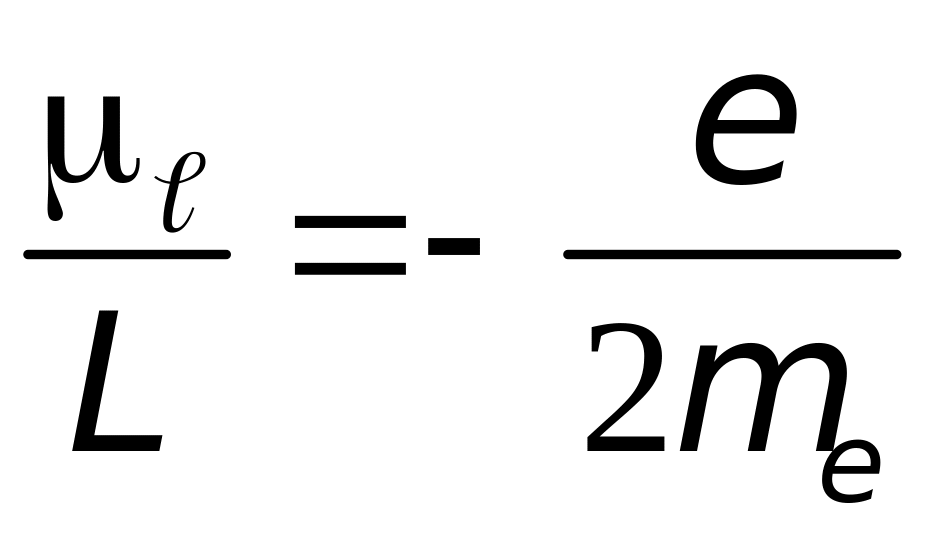причем, векторы магнитного и механического моментов направлены в противоположные стороны. Для магнитного момента получим:

,

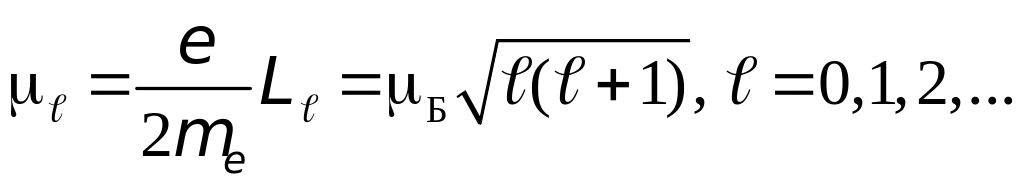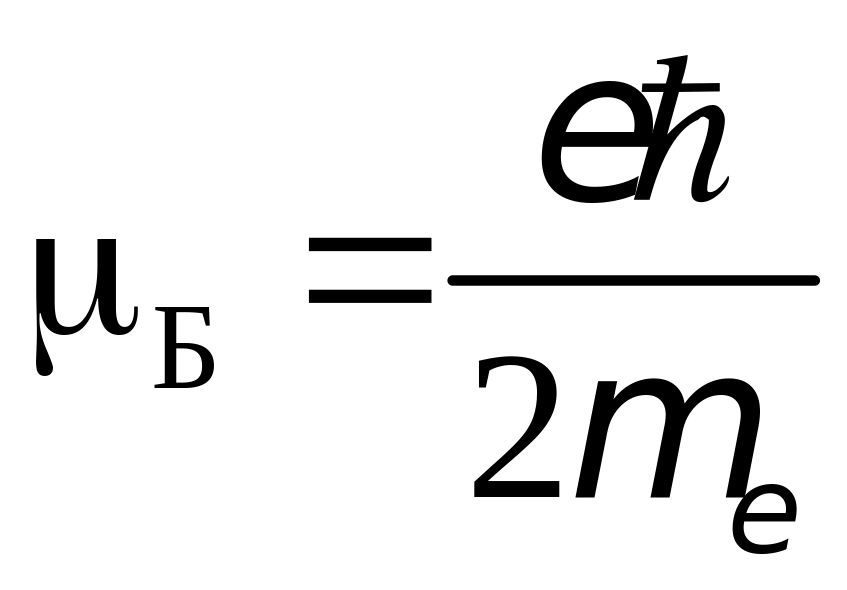где –магнетон Бора: ,а для проекции магнитного момента на произвольную ось :

Квантование проекции магнитного момента атомов было обнаружено экспериментально Штерном и Герлахом, схема опыта которых изображена на

Р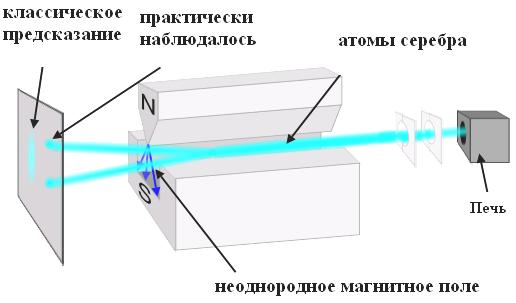 ис.19.

Рис.19 Опыт Штерна и Герлаха

Пучок атомов серебра пропускали через неоднородное магнитное поле, создаваемое мощным постоянным магнитом. На магнитные моменты атомов действовала сила, зависящая от проекции момента на направление магнитного поля и отклонявшая летящие атомы от их первоначального направления движения. При хаотичной (непрерывной), ориентации магнитных моментов атомов на расположенной далее по направлению движения атомов фотопластинке должна была проявиться размытая полоса. Вместо этого на ней образовались две чёткие узкие полосы, говорившие о том, что магнитные моменты атомов пучка принимали лишь два определённых значения, что и подтвердило квантование магнитного момента атомов.