Теорема Кронекер-Капелли

Реализуя метод Гауса после приведения основной матрицы системы можно делать выводы содержащиеся в следующей теореме:

Система линейных алгебраических уравнений (1) совместна тогда и только тогда когда r(A)=r(A’), при этом в случае выполнения условий теоремы возможны ситуации:

1. r(A)=r(A’)=n – система определена т.е. имеет единственное решение.

2. r(A)=r(A’)<n – система (1) неопределенна т.е. имеет бесконечно много решений.

Для нахождения общего решения системы следует n-r(A) считать свободными

Обобщенный метод Гауса

Обобщенный метод Гаусса основывается на матричной записи системы (1) и разложений основной матрицы системы в произведение простейших. Пользуясь этим, получаем:

Ax=B₀

A=BDrC

BDrCx=B₀

Cx=Y; x=C^-1Y

BDrY=B₀

DrY=B^-1B₀

Таким образом для решения исходной системы следует решить такую матричную систему:

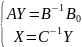которую находим реализуя

ОПРЕДЕЛИТЕЛИ

Подстановки и перестановки n-степени

Пусть дан отрезок натурального ряда {1,2,…,n}. Назовем перестановкой порядка n любое расположение элементов этого множества.

Обозначим через Pn – число перестановок порядка n. Можно показать, что Pn=n!, n!=(n-1)…2*1

P₃=3!=3*2*1=6

Пусть дана перестановка порядка n: n₁, n₂,…n_k…n_j…n_n

n_k, n_j совершают инверсию n_k>n_j

ОПРЕДЕЛЕНИЕ:

Перестановку называют четной (нечетной), если общее число инверсий совершаемых всеми символами этой перестановки четно (нечетно).

ЛЕММА:

Если в перестановке поменять местами любые 2 символа, то четность перестановки изменяется на противоположную.

ОПРЕДЕЛЕНИЕ:

Подстановкой называют взаимноодназначное отображение множества {1,2,…,n} на себя.

Подстановки принято записывать:

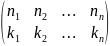
Отметим что разных подстановок существует n!

Среди разнообразных форм записи одной и той же подстановки будем выделять каноническую, которая характеризуется тем, что первая строка записана в естественном порядке.

ОПРЕДЕЛЕНИЕ:

Подстановка называется четной (нечетной) если ее строки имеют одинаковую (разную) четность.

Определение определителя

Рассмотрим квадратную матрицу порядка n

А= Ее определителем называют число, которое сопоставляется этой матрице по правилам:

I) Определитель есть сумма произведений n ее элементов выбранных так что:

1) Каждый элемент выбирается так, что бы он содержался только в одной строке и в одном столбце.

2) Каждое произведение берется со знаком определяемым четностью подстановки образуемой номерами сомножителей: (-1)^τ

Обозначается определитель: det A, ∆_A

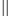
Таким образом: det A = ∑(+- )

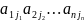Определители второго порядка

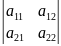=+а₁₁а₂₂-а₁₂а₂₁

Определители третьего порядка

=

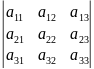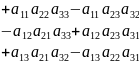
Правило треугольника вычисления определителя 3-го порядка

Формула для вычисления определителя третьего порядка = может быть интерпретирована:

Правило Саррюса

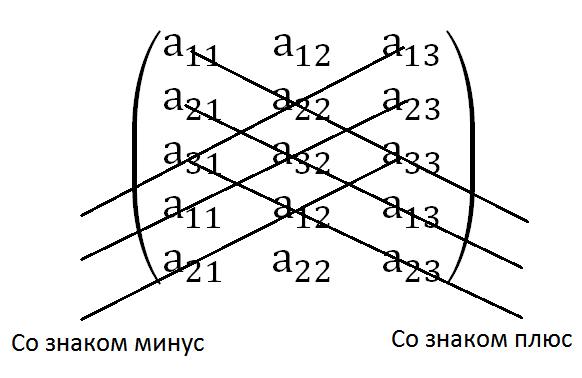
Свойство определителя

1) Определитель матрицы при ее транспонировании совпадают.

ДОКОЗАТЕЛЬСТВО: Это утверждение следует из определения

det A = det A^τ

det A = ∑(+- )

det A^τ = ∑(+- )

Определители det A b det A^τ состоят из сумм произведений одних и тех же элементов взятых с одинаковыми знаками, поэтому эти определители равны.

СЛЕДСТВИЕ: строки и столбцы определителя равноправны, т.е. если некоторое утверждение имеет смысл для строки, то оно справедливо для столбца и наоборот.

2) Если некоторая строка(столбец) определителя содержит только нулевые элементы, то такой определитель равен 0.

3)Если поменять местами любые две строки (столбца) определителя, то знак определителя изменится на противоположный.

ДОКОЗАТЕЛЬСТВО:

det A = ∑+-

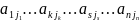
det = ∑+-

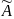C^jk(↗↖)C^js, => det A= - det

4)Если две строки (столбца) определителя одинаковы, то он равен нулю.

ДОКОЗАТЕЛЬСТВО(его вариант): Пусть в определители строки с номерами k и s одинаковы. Поменяем их местами, тогда с одной стороны получим такой же определитель, а с другой в силу свойства 3) должен быть противоположный знак.

det A = 0 => det A = 0

ДОКОЗАТЕЛЬСТВО(более понятное): Пусть А исходная матрица с двумя одинаковыми строками. Поменяем их местами. Получим матрицу А’=А. По свойству 3) |A’|= -|A|, но с другой стороны |A’|= |A|, т.к. А’=A => |A|= -|A| => |A| = 0

5)Если какую либо строку (столбец) определителя умножить на некоторое число k то и весь определитель умножится на это число k.

СЛЕДСТВИЕ 1: общие множители можно выносить за знак определителя

СЛЕДСТВИЕ 2: если две каких-либо строки(столбца) пропорциональны, то такой определитель будет равен 0

6)Если какая-либо строка(столбец) определителя может быть представлена в виде суммы строк(столбцов), то такой определитель равен сумме двух определителей, все строки(столбцы) которых, кроме выделенной, совпадают со строками(столбцами) исходного определителя, а в выделенной строке(столбце) стоит для первого определителя первое слагаемое, для второго второе.

= +

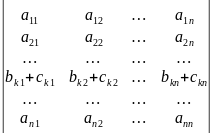СЛЕДСТВИЕ: величина определителя не изменится, если к любой его строке(столбцу) добавить любую другую строку(столбец) умноженную на произвольное число.

7)Определитель произведения квадратных матриц, равен произведению их определителей.

det A*B= det A * det B

8)Определитель треугольной матрицы равен произведению диагональных элементов.

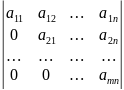= a₁₁*a₂₂*…*a_mn

СЛЕДСТВИЕ 1: Определитель единичной матрицы равен 1

СЛЕДСТВИЕ 2: Если матрица обратима, то ее определитель не равен 0 и связан с определением обратной матрицы соотношением

detA^-1 = (detA)^-1 или detA^-1= 1/detA

из свойства АА^-1=En => detA*detA^-1=1