5 Задание

1. Если функция (x,y) – неотрицательна и интегрируема в области G , то геометрический смысл интеграла _G(x,y)dxdy есть объём цилиндрического тела Q, ограниченного поверхностью , образующие которой параллельны оси OZ , а направляющей служит граница области G

2. Статический момент M_OX относительно оси OX пластинки G, с плотностью (x,y), (x,y)G, равен M_OX=_Gy(x,y)dxdy

3. Геометрический смысл _Gdxdy есть площадь плоской фигуры , занимающей область G

4. Статический момент M_OY относительно оси OY пластинки G с плотностью (x,y), ((x,y)G) равен M_OY=_Gx(x,y)dxdy

5. Абсцисса центра тяжести пластинкиGR² с заданной плотностью (x,y) , ((x,y)G) равна ==(_Gx(x,y)dxdy)/(_G(x,y)dxdy)

6. Моменты инерции I_X, I_Y пластинки GR² с плотностью (x,y) , ((x,y)G) равны I_X=_Gy²(x,y)dxdy, I_Y=_Gx²(x,y)dxdy

7. Если (x,y) , (x,y)G, - плотность распределения масс, то механический смысл интеграла _Gx(x,y)dxdy есть статический момент пластинки G относительно OY

8. Момент инерции I_O относительно начала координат пластинки GR² с плотностью (х,у), (x,y)G, равен I_O=_G(x²+y²)(x,y)dxdy

9. Согласно геометрическому смыслу двойного интеграла объем замкнутой области V={(x,y,z):(x,y)G, (x,y) z  (x,y)}, где функции  и  интегрируемы в G, равен _VfdV=_G(_(x,y)^(x,y)(x,y,z)dz)dxdy

10. Если (х,у), ((x,y)G) - плотность распределения масс, то механический смысл интеграла _Gy²(x,y)dxdy есть момент инерции пластинки относительно OX

6 Задание

1. По определению криволинейным интегралом первого рода от функции f(x,y), непрерывной на кусочно-гладкой кривой АВ, называется интеграл по длине дуги АВ , его обозначение _AB(x,y)d

2. Согласно геометрическому смыслу тройного интеграла, объем области VR³ вычисляется по формуле V=_Vdxdydz

3. Статический момент М_XY относительно плоскости XOY тела VR³ с плотностью (х,у,z), ((x,y,z )V) равен М_XY=_Vz(x,y,z)dxdydz

4. Абсцисса центра тяжести телаVR³ с плотностью (х,у,z), (х,у,z)V равна 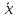=M_yz/M=(_Vx(x,y,z)dxdydz)/(_V(x,y,z)dxdydz)

5. Геометрический смысл тройного интеграла _VdV есть объём области V

6. Если область V={(x,y,z):(x,y)G,(x,y)z(x,y)}, где функции  и  интегрируемы в G, то _VdV равен двойному интегралу вида: _G((_(x,y)^(x,y)(x,y,z)dz)dxdy

7. Момент инерции I_OX относительно оси ОХ тела VR³ с плотностью (x,y,z), (x,y,z)V, равен I_OX=_V(y²+z²)(x,y,z)dxdydz

8. Ордината центра тяжести телаVR³ с плотностью (x,y,z), (x,y,z)V, равна =M_ZX/M=(_Vy(x,y,z)dxdydz)/(_V(x,y,z)dxdydz)

9. Момент инерции I_Z относительно оси Oz тела VR³ с плотностью (x,y,z), (x,y,z) V, равен I_Z=_V(x²+y²)(x,y,z)dxdydz

10. Аппликата центра тяжести телаV R³ с плотностью (x,y,z), (x,y,z) R³ равна =M_XY/M=(_Vz(x,y,z)dxdydz)/(_V(x,y,z)dxdydz)