
§11. Ряды Фурье.
Далее мы будем рассматривать глобальное разложение, то естьна конечном отрезке[a,b].
Определение. Понятие ортогонольных и нормированных систем ф-ий:
(х), (х)
интегрируемые при х[a,b],
тогда
![]() (*)
-cкалярное произведение.
(*)
-cкалярное произведение.
для (*) вып-ся аксиомы ск-го произведения:
А.1 (,)=(,)
А.2 (,)=(,)=(,),=const
А.3 (,1+2)=(,1)+(,2)
Определение:Функцииина[a,b]ортогональны если
(,)=0,
т.е.
![]() (х)(х)dx=0.
(х)(х)dx=0.
Определение.
Понятие нормированности:=![]() - норма (длина вектора).
- норма (длина вектора).
Докажем, что норма обладает всеми св-вами длины:
=[![]() 2(x)dx]0.5
2(x)dx]0.5
A.1 0, =0 0
A.2 =, R1
A.3 1+2=1+2
Определения:Если для системы функций1,2,...,nвведено понятие нормы, то такая система наз-ся нормированной. Если норма каждого элемента пространства равна 1, то наз-ся нормированной на 1. Если система функций попарно ортогональна и нормированная на 1, то такая система наз-ся ортонормированной: ОН - ортонормированная система, если
 ;
ОН
;
ОН ![]()
Пример:приx[-,]
{1,cosx,sinx,cos2x,sin2x,...,
cosnx,sinnx}.
![]()
![]()
![]() .
Аналогично
.
Аналогично
![]() sin(nx)sin(mx)dx=0;
sin(nx)sin(mx)dx=0;![]() sin(nx)cos(mx)dx=0.
Найдем норму:cosnx=
sin(nx)cos(mx)dx=0.
Найдем норму:cosnx=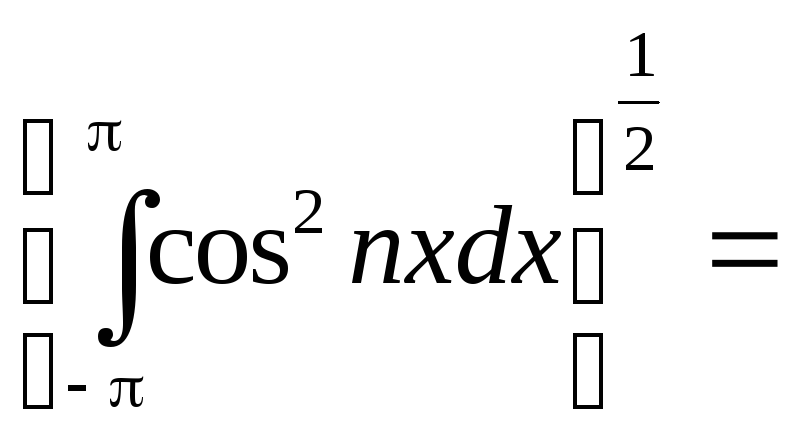
 .
Аналогичноsin(nx)=
.
Аналогичноsin(nx)=![]() .Получаем
ОН систему:
.Получаем
ОН систему:
![]()
![]()
Ряд Фурье. Коэфициенты Фурье по ОН системе.
{1(x),2(x),...,n(x)}
- ОН система, т.е.
 .f(x)=
.f(x)=![]() fnn(x)
- ряд Фурье, гдеfn
- коэфициенты. Умножим обе части
этого уравнения наm(x)и проинтегрируем:
fnn(x)
- ряд Фурье, гдеfn
- коэфициенты. Умножим обе части
этого уравнения наm(x)и проинтегрируем:
![]() f(x)m(x)dx==
f(x)m(x)dx==![]() m(x)
m(x)
![]() fnn(x)dx=
fnn(x)dx=![]() fn
fn![]() m(x)n(x)dx=0
- когдаmn.
Когдаm=n:
m(x)n(x)dx=0
- когдаmn.
Когдаm=n:
=fn(n,n)=fn=![]() f(x)n(x)dx
f(x)
f(x)n(x)dx
f(x)
![]() (f,n)n(x)
(f,n)n(x)
Ряд Фурье для тригонометрических функций.
![]()
![]() ,
f(x)
,
f(x) ![]() (ancos(nx)+bnsin(nx))(4)
(ancos(nx)+bnsin(nx))(4)
где an=![]() f(x)cos(nx)dx,bn=
f(x)cos(nx)dx,bn=![]() f(x)sin(nx)dx,
n=0,1,2,...
f(x)sin(nx)dx,
n=0,1,2,...
Определение:Функция наз-ся кусочно-непрерывной на данном отрезке, если этот отрезок можно разбить на конечное число интегралов, в каждом из которых функция непрерывна.
Т-ма Дирихле:Пустьf(x)
1)определена для всех х[-,]
2)кусочно-непрерывная на[-,]
3)кусочно-монотонная на[-,]
4)ограничена на [-,], тогда она разложима в тригонометрический ряд Фурье (4). Если точка х[-,]и в этой точкиf(x)непрерывна, то сумма ряда
S(x)=![]() (ancos(nx)+bnsin(nx))=f(x).
Если точка х - точка разрыва, скачок,
тоS(x)=1/2
[f(x-0)+f(x+0)]
(ancos(nx)+bnsin(nx))=f(x).
Если точка х - точка разрыва, скачок,
тоS(x)=1/2
[f(x-0)+f(x+0)]
S(-)=S()=1/2 [f(+0)+f(-0)]
Замечания:1)поведение функцииfза пределами[-,]может в корне отличаться от значенияS.
2)если мы хотим разложитьfна всей действительной оси, то соглас- но (4) мы должны продол- жить пе- риодическим образом с периодом 2.
Пример:f(x)=x, x[-,]

a0=![]() xdx=0
xdx=0
![]()
Разложение функций в тригонометрические ряды на произвольном промежутке.
Часто возникает задача разложения функций в тригонометрический ряд на произвольном промежутке
y[a,b] (a,b < ,a < b)
x=y+; [-,] переходит в[a,b].
 ,
,![]() m,
f(y+)=f*(y);
dx=dy,
an=
m,
f(y+)=f*(y);
dx=dy,
an=![]() f*(y)cosn(y+)dy
f*(y)cosn(y+)dy
bn=![]() f*(y)sinn(y+)dy,
f*(y)=
f*(y)sinn(y+)dy,
f*(y)=![]() +
+![]() (ancosn(y+)+bnsinn(y+))
(ancosn(y+)+bnsinn(y+))
Разложив cos и sin по формулам:
f*(y)=![]() +
+![]() (a*ncosny+b*nsinny),
где нужно вычислитьa*n
, b*n
и a*0
.
(a*ncosny+b*nsinny),
где нужно вычислитьa*n
, b*n
и a*0
.
Примеры:1) a=0, b=L >0
x=![]()
![]()
![]()
![]()
a= - L, b= L
x=![]()
Разложение четных функций в тригонометрический ряд.
f(x)=f(-x) , xR1
an=![]() f(x)cosnxdx=
f(x)cosnxdx=![]() f(x)cosnxdx
f(x)cosnxdx
bn=0
f(x)=
![]() +
+![]() ancosnx
- разложение по косинусам.
ancosnx
- разложение по косинусам.
Разложение нечетных функций в тригонометрический ряд.
f(x)= - f(-x); a0=0, an=0
f(x)=
![]() bnsinnx
bnsinnx
bn=![]() f(x)sinnxdx
f(x)sinnxdx
- разложение по синусам.
Примеры:1)f(x)=x
a0=![]() 1dx=2;
an=
1dx=2;
an=![]() 1cosnxdx=0
1cosnxdx=0
f(x)=
![]() =1
=1
2) Функция
![]()
bn=![]() 1sinnxdx=
1sinnxdx=![]()
Разложение функций в ряд по синусам в несимметричном промежутке (0, L).
f(x) , x[0, L]. Доопределим функцию на промежутке[-L,0] (нечетным образом)
В ряд по синусам.
f(x)=
![]() bnsin
bnsin![]() ,
где
,
где
bn=![]() f(x)sin
f(x)sin![]() dx
dx
В ряд по косинусам (четным образом).
f(x)=
![]() +
+![]() ancos
ancos![]() ,
где
,
где
an=![]() f(x)cos
f(x)cos![]() dx
dx
Пример:по синусам
f(x)=x, x[0,1], L=1
![]()
![]()
![]()
