§2 Производные и дифференциалы высших порядков

1.Производные высших порядков

Опр. f(x) определена на (a,b) и имеет в некоторой окрестности точки x₀(a,b) производную g(x)=f(x). Если в точке x₀ g( x₀), то она называется производной второго порядка от f в точке x₀ и обозначается f(x₀). Производной n-го порядка называется производная от производной n-1 го порядка

.

Обозначение Лейбница

Отметим, что для существования n-ой производной в точке, (n-1) - ая производная должна существовать в некоторой окрестности.

f называется n-раз дифференцируемой на X, если в каждой точке X существует n-ая производная.

f называется n-раз непрерывно дифференцируемой на X, если n-ая производная на X существует и непрерывна на X.

КлассыCⁿ(X),Cⁿ[a,b].

Пример. Вычисление старших производных функции, заданной параметрически

, x(t) строго монотонна

Аналогично первой производной определяются односторонние производные высших порядков.

2. Формула Лейбница

Индукция по n.

3.Дифференциалы высших порядков

dx=x, dy=f(x₀)dx, x-независимое переменное

Опр. d²f=fdx², dx=x, dⁿf=d(d^n-1f)=d(f^(n-1)dx^n-1)=f⁽ⁿ⁾dxⁿ

при вычислении последующих дифференциалов приращение dx=x берется одно и тоже. Из определения следует, что

, что согласуется с определением Лейбница.

Замечание. Если x – независимое переменное, то dⁿ x = 0, n=2,3,…

Простейшие свойства дифференциалов

1. d(u+v)=du+dv,d(uv)=udv+vdu , d(u/v)=(vdu - udv)/v²

2. dⁿ(cu)=cdⁿu, c=const

3. dⁿ(u+v)=dⁿu+ dⁿv

4. 

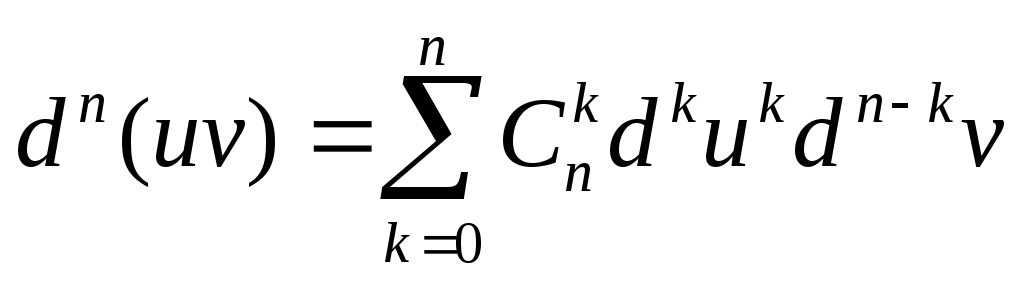
4.Инвариантность формы дифференциала первого порядка

y=f(x),x=g(t)

dy=(f(g(t))dt=f(x)g(t)dt=f(x)dg=f(x)dx

здесь x – является независимой переменной. Для высших порядков инвариантности нет.

dy=fdx, d²y=fdx²+fd²x, x=t², d²x0

Замечание. Частный случай ( когда инвариантность есть )

dⁿy, y=f(x), x=at+b, dx = a dt, d²x=…=dⁿx=0

dⁿf=f⁽ⁿ⁾dxⁿ, хотя x не является независимым переменным.

§3 Теоремы о среднем для дифференцируемых функций

1.Теорема Ферма о нуле производной

Теорема. f – определена на (a,b) и дифференцируема в точке x₀(a,b), принимает в точке x₀ наибольшее или наименьшее значение. Тогда f(x₀)=0.

Доказательство. Наименьшее значение

f(x₀+0)0, f(x₀-0)0  f(x₀)=0

Геометрическая интерпретация

2.Теорема Ролля о нуле производной

Теорема. f непрерывна на [a,b], дифференцируема на (a,b), f(a)=f(b). Тогда(a,b):f()=0.

Доказательство. Хотя бы одна из₁, ₂ внутренняя.

3.Теорема Лагранжа о конечных приращениях

Теорема. f непрерывна на [a,b], дифференцируема на (a,b). Тогда

(a,b):f(b)-f(a)=f()(b-a).

Доказательство.

. Геометрическая интерпретация.

Следствие 1.Если f непрерывна на [a,b], дифференцируема на (a,b) и f(x)0 на (a,b), то f(x)const. Применить теорему к [x₀,x].

Следствие 2.Если f непрерывна на [a,b], дифференцируема на (a,b) и f(x)=g(x) на (a,b), то f(x)=g(x)+ const.

4.Теорема Коши о конечных приращениях

Теорема. Если f, g непрерывны на [a,b], дифференцируемы на (a,b), то существует (a,b):g()(f(b)-f(a))=f()(g(b)-g(a)).

Доказательство. ПоложимF(x)=g(x)(f(b)-f(a))-f(x)(g(b)-g(a)), F(a)=F(b).

Следствие. Если g(x)0 на (a,b), то

Доказательство. g(x)0g(b)-g(a) 0

§4 Правило Лопиталя

Конспект лекций Логинов А.С. ЭТФ 1 семестр [e-mail]