Глава III ряды

§ 1. Числовые ряды

Пусть u₁,u₂,u₃,…u_n,…— бесконечная числовая по­следовательность. Выражение

u₁+u₂+u₃+…..+u_n+…

называется бесконечным числовым рядом, а числа u₁,u₂,u₃,…u_n,….— членами ряда; и_п=f(п) называется общим членом. Ряд часто записывают в виде .

Сумму первых п членов числового ряда обозначают через S_n и называют n-й частичной суммой ряда:

S_n= u₁+u₂+u₃+…..+u_n.

Ряд называется сходящимся, если его n-я частичная сумма S_n при неогра­ниченном возрастании п стремится к конечному пределу, т. е. если

Число S называют суммой ряда. Если же n-я частичная сумма ряда при не стремится к конечному пределу, то ряд называют расходящимся.

Ряд а+aq+aq²+…+aq^n-1+…(|q|<1),

составленный из членов любой убывающей геометрической прогрессии, яв­ляется сходящимся и имеет сумму a/(1—q).

Ряд

называемый гармоническим, расходится.

Приведем основные теоремы о сходящихся числовых рядах.

1. Если сходится ряд

u₁+u₂+u3+…,

то сходится и ряд

u_m+1+u_m+2+u_m+3+…

получаемый из данного ряда отбрасыванием первых т членов (этот последний ряд называют т-м остатком исходного ряда); наоборот, из сходимости т-го остатка ряда вытекает сходимость данного ряда.

2. Если сходится ряд

u₁+u₂+u₃+…,

и суммой его является число S, то сходится и ряд

au₁+au₂+au₃+…,

причем сумма последнего ряда равна аS.

3. Если сходятся ряды

u₁+u₂+u₃+…,

имеющие соответственно суммы S и , то сходится и ряд

причем сумма последнего ряда равна S +.

4. Если ряд

u₁+u₂+u₃+…

сходится, то при предел общего члена сходящегося

ряда равен нулю (необходимый признак сходимости ряда).

Таким образом, если , то ряд расходится.

Перечислим важнейшие признаки сходимости и расходимости рядов с по­ложительными членами.

Первый признак сравнения. Пусть даны два ряда

(1)

и

(2)

причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т. е. (n=1, 2, 3, ...). Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).

Этот признак остается в силе, если неравенства выполняются не при всех n, а лишь начиная с некоторого номера n = N.

Второй признак сравнения. Если существует конечный и от-

личный от нуля предел то оба ряда и одновременно сходятся или одновременно расходятся.

Признак Коши. Если для ряда

существует , то этот ряд сходится при С < 1 и расходится

при С > 1.

Признак Даламбера. Если для ряда

существует = D, то этот ряд сходится при D< 1 и расходится

при D > 1.

Интегральный признак. Если F(х) при —непрерывная, положительная и монотонно убывающая функция, то ряд где u_n=f(n), сходится или расходится в зависимости от того, сходится или расходится интеграл

Рассмотрим теперь ряды, члены которых имеют чередующиеся знаки, т. е. ряды вида

где u_n>0 (n=1, 2, 3, ...),

Признак сходимости знакочередующегося ряда (приз­нак Лейбница). Знакочередующийся ряд сходится, если абсолютные вели­чины его членов монотонно убывают, а общий член стремится к нулю, т. е. если выполняются следующие два условия: 1) и_г > и₂ > и₃ >... и 2)

Возьмем n-ю частичную сумму сходящегося знакочередующегося ряда, для которого выполняется признак Лейбница:

Пусть R_n—n-й остаток ряда. Его можно записать как разность между сум­мой ряда S и п-й частичной суммой S_n т. е. R_n=S-S_n Нетрудно видеть, что

Величина | |оценивается с помощью неравенства | | < u_n+1

Остановимся теперь на некоторых свойствах знакопеременных рядов

(т. е. знакочередующихся рядов и рядов с произвольным чередованием знаков

своих членов).

Знакопеременный ряд

сходится, если сходится ряд

В этом случае исходный ряд называется абсолютно сходящимся.

Сходящийся ряд называется условно сходящимся, если ряд расходится.

Если ряд абсолютно сходится, то ряд, полученный после любой перестановки бесконечного множества его членов, абсолютно сходится и имеет ту же сумму, что и первоначальный ряд.

Если ряд условно сходится, то при перестановке бесконечного множества его членов сумма ряда может измениться. В частности, при соот­ветствующей перестановке членов условно сходящегося ряда можно превра­тить его в расходящийся ряд.

Если ряды и сходятся абсолютно и имеют соответственно суммы S1 и S₂, то сходится абсолютно и ряд

Этот ряд называется произведением рядов (по Коши). Его сумма равна S₁S₂.

269. Дан общий член ряда . Написать первые че­тыре члена ряда.

Если n=1, то u₁=1/11; если n=2, то u₂=2/101; если n=3, то u₃=3/1001; если n= 4, то u₄ = 4/10001;….. Ряд можно записать в виде

270. Найти общий член ряда

Последовательные числители образуют арифметическую прогрессию 1, 3, 5, 7 ...; n-й член прогрессии находим по формуле a_n=a₁+d(n-1). Здесь а₁=1, d=2 поэтому a_n=2п—1. Последовательные знаменатели обpазуют геометрическую прогрессию 2, 2², 2³, 2⁴, ...; n-й член этой прогрессии b_n=2ⁿ. Следовательно, общий член ряда и_п = (2п—1)/2ⁿ.

Вообще нужно иметь в виду, что несколько первых членов ряда полностью ряд не определяют.

270. Найти общий член ряда

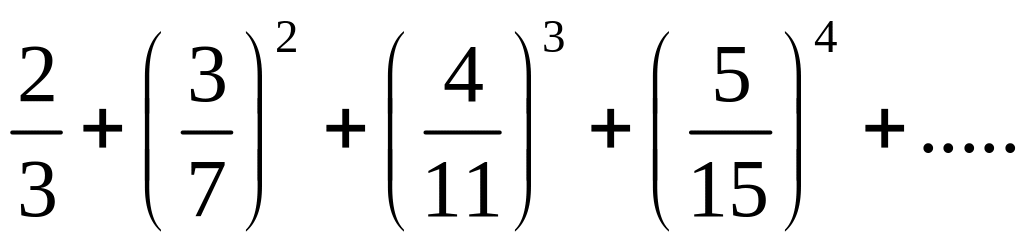
Показатель степени каждого члена совпадает с номером этого члена, поэтому показатель степени п-го члена равен п. Числители дробей 2/3, 3/7, 4/11, 5/15,... образуют арифметическую прогрессию с первым членом 2 и разностью 1. Поэтому п-й числитель равен n+1. Знаменатели образуют арифметическую прогрессию с первым членом 3 и разностью 4. Следовательно, n-й знаменатель равен 4n-1. Итак, общим членом ряда является

272. Найти сумму ряда

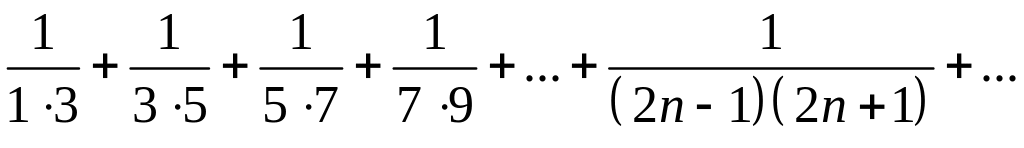
Общий член ряда можно представить в следующем виде:

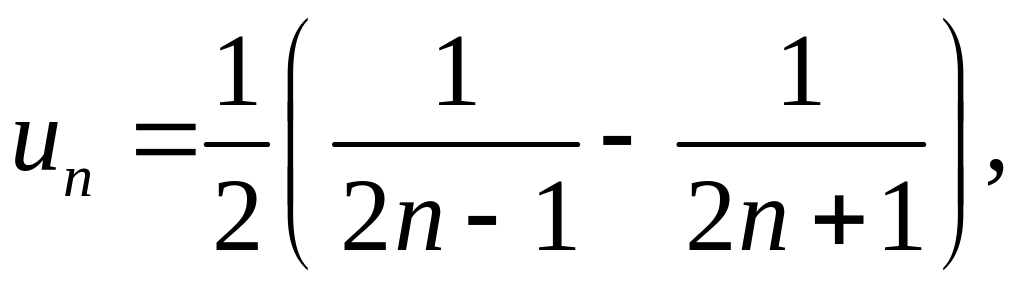
откуда

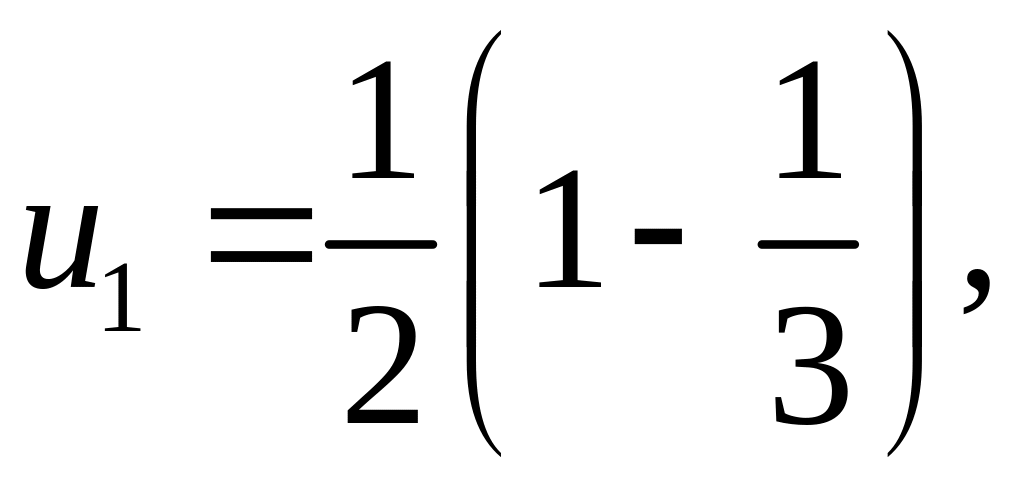
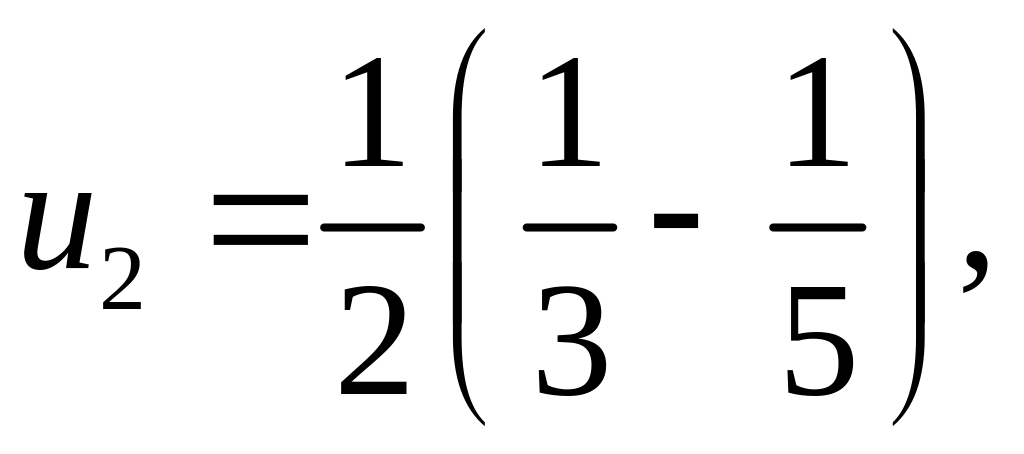
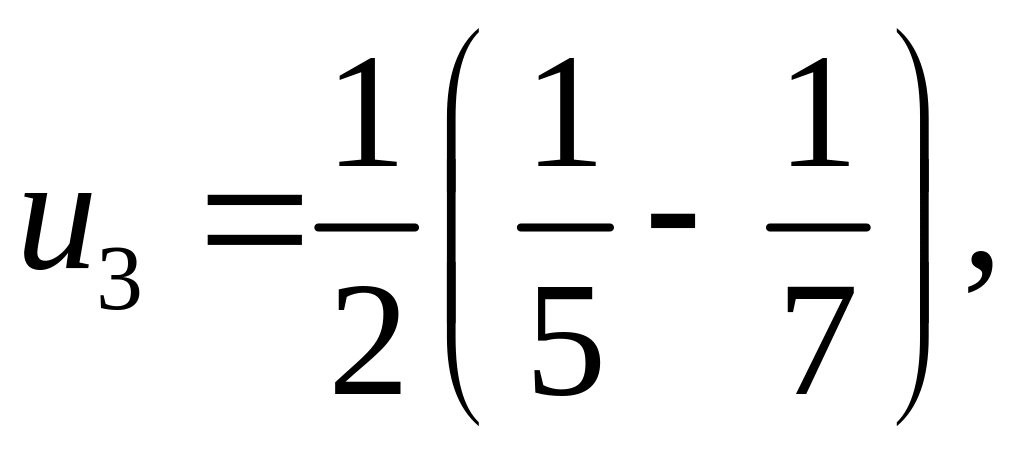
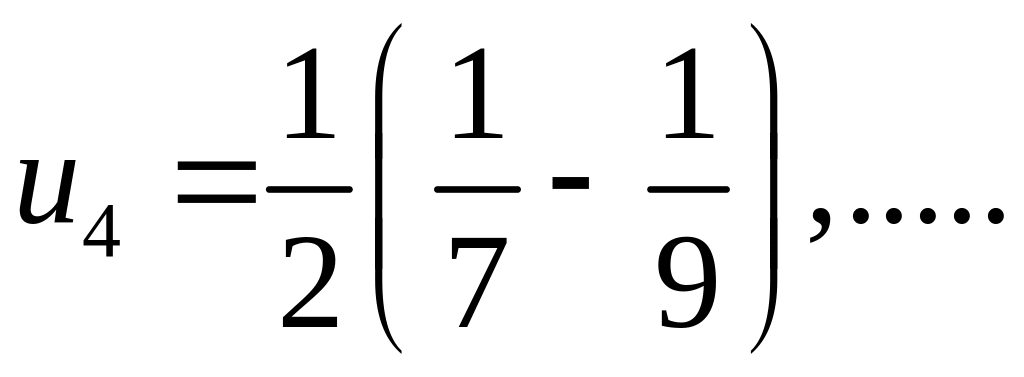
Следовательно,

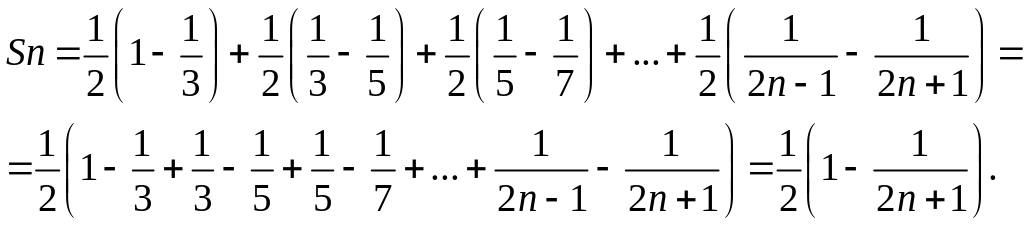
Так как 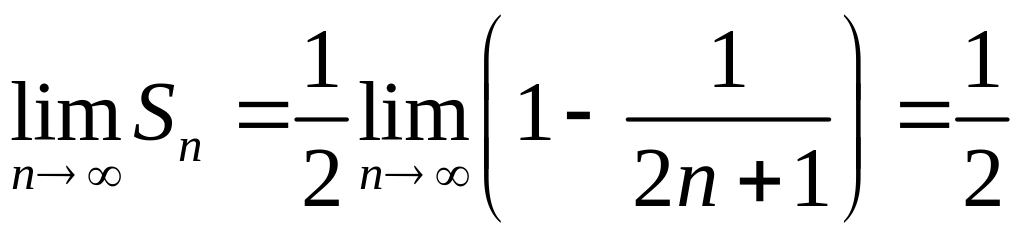, то ряд сходится и его сумма равна 1/2.▲