
- •Глава III ряды
- •§ 1. Числовые ряды
- •2. Если сходится ряд
- •273. Найти сумму ряда
- •Исследовать сходимость ряда
- •§ 2. Функциональные ряды
- •3. Степенные ряды
- •§ 4. Разложение функций в степенные ряды
- •§ 5. Приближенные вычисления значений функций с помощью степенных рядов
- •§ 6. Применение степенных рядов к вычислению пределов и определенных интегралов
- •428. Найти
- •§ 7. Комплексные числа и ряды с комплексными членами
- •3. Показательная и тригонометрические функции комплексного переменного.
- •§ 8. Ряд фурье
- •§ 9. Интеграл фурье
3. Степенные ряды
Функциональный ряд вида
a0+a1(x-a)+a2(x-a)2+…+an(x-a)n
где a0 , a1,… an - действительные числа, называется степенным.
Основное свойство степенных рядов состоит в том, что если степенной ряд сходится при х=х0, то он сходится (и притом абсолютно) при всяком значении х, удовлетворяющем неравенству|х—а| < |х0—а| (теорема Абеля).
Одним из следствий теоремы Абеля является факт существования для всякого степенного ряда интервала сходимости |х—а| < R, или а—R < х < a+R с центром в точке а, внутри которого степенной ряд абсолютно сходится и вне которого он расходится. На концах интервала сходимости (в точках x= а ± R) различные степенные ряды ведут себя по-разному: одни сходятся абсолютно на обоих концах, другие—либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом расходятся, третьи— расходятся на обоих концах.
Число R—половина длины интервала сходимости—называется радиусом сходимости степенного ряда. В частных случаях радиус сходимости ряда R может быть равен нулю или бесконечности. Если R = 0, то степенной ряд сходится лишь при х=а; если же R = ∞, то ряд сходится на всей числовой оси.
Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов.
Если среди коэффициентов ряда a1,a2…anнет равных нулю, т. е. ряд содержит все целые положительные степени разности х—а, то
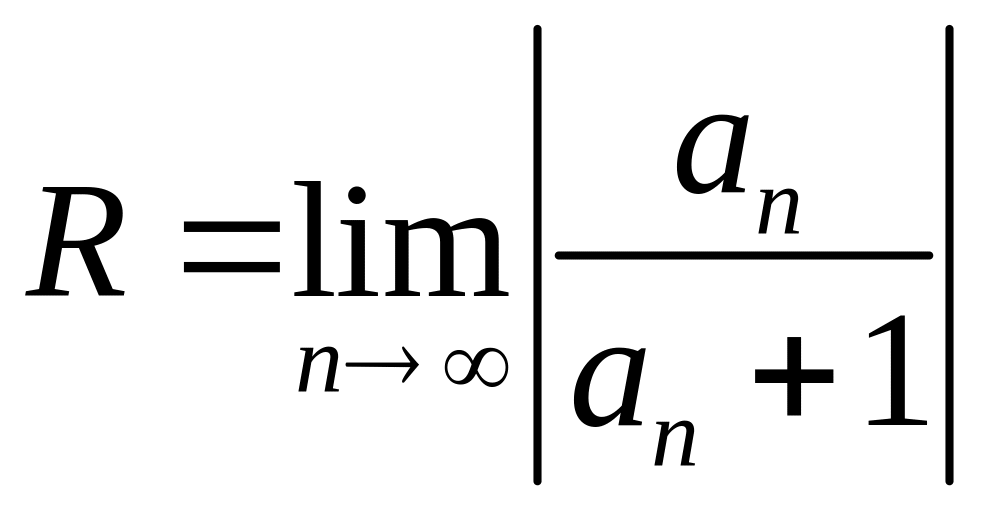 (1)
(1)
при условии, что этот предел (конечный или бесконечный) существует.
2. Если исходный ряд имеет вид
![]() ....
(где р—некоторое
определенное целое положительное число:
2, 3, ...), то
....
(где р—некоторое
определенное целое положительное число:
2, 3, ...), то
 (2)
(2)
Если среди коэффициентов ряда есть равные нулю и последовательность оставшихся в ряде показателей степеней разности х—а любая (т. е. не обра зует арифметическую прогрессию, как в предыдущем случае), то радиус схо димости можно находить по формуле
 (3)
(3)
в которой используются только значения an отличные от нуля. (Эта формула пригодна и в случаях 1 и 2.)
4. Во всех случаях интервал сходимости можно находить, применяя не посредственно признак Даламбера или признак Коши к ряду, составленному из абсолютных величин членов исходного ряда.
Записав ряд в виде
![]()
(здесь и0 = а0, ип(х)=ап(х—а)N, где зависимость N от п может быть любой, причем через ап обозначен не коэффициент при (х—а)", а коэффициент n-го члена ряда), находят интервал сходимости из неравенств

Отметим следующее свойство степенных рядов: ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот оке интервал сходимости и их сумма внутри интервала сходимости равна соответственно производной и интегралу от суммы первоначального ряда.
Таким
образом, если
 ,
то
,
то
 ,
,

где —R < х—а < R.
Операцию почленного дифференцирования и интегрирования можно производить над степенным рядом сколько угодно раз. Следовательно, сумма степенного ряда внутри его интервала сходимости является бесконечно дифференцируемой функцией.
357. Исследовать сходимость степенного ряда
![]()
∆ Здесь ап=1/п, ап+1= 1/(n+ 1). Найдем радиус сходимости ряда:

Следовательно, ряд сходится для значений х, удовлетворяющих неравенству —1 < х < 1.
Исследуем
сходимость ряда на концах промежутка.
Если х=1,
то
получаем
гармонический ряд
![]() который, как известно, расходится. Если
х=-1,
то получаем ряд
который, как известно, расходится. Если
х=-1,
то получаем ряд
![]() Этот ряд сходится,
так как удовлетворяет условиям признака
Лейбница.
Этот ряд сходится,
так как удовлетворяет условиям признака
Лейбница.
Итак, область сходимости степенного ряда определяется двойным неравенством -1≤x<1.▲
358. Исследовать сходимость ряда
![]()
∆ Здесь an =1/n2 , an+1 =1/(n+1)2, имеем

Следовательно, ряд сходится, если —1 < x — 2 < 1, т. е. 1 < х < 3.
Исследуем
сходимость ряда на концах промежутка.
Если х = 3, то получаем ряд
![]() который сходится, так как ряд
который сходится, так как ряд
![]() сходится
при
р
> 1
(на основании интегрального признака).
сходится
при
р
> 1
(на основании интегрального признака).
Если
х=1,
то
получаем ряд
![]() Этот ряд сходится
(и
притом абсолютно), так как сходится ряд
из абсолютных величин его членов. Итак,
степенной ряд сходится для значений х,
удовлетворяющих
двойному
неравенству 1 ≤ х
≤
3.
▲
Этот ряд сходится
(и
притом абсолютно), так как сходится ряд
из абсолютных величин его членов. Итак,
степенной ряд сходится для значений х,
удовлетворяющих
двойному
неравенству 1 ≤ х
≤
3.
▲
359. Исследовать сходимость ряда
![]()
∆ Здесь аn=n!, аn+1=(n+1)!; значит,

Ряд сходится только при x—5 = 0, т. е. в точке х=5. ▲
360. Исследовать сходимость ряда

∆ Имеем аn=n!, аn+1=(n+1)!, аn = 0;
![]()
Следовательно, ряд сходится при любом значении х. Отсюда, между прочим, заключаем, что предел общего члена ряда при любом значении х равен нулю,
т. е.
 .▲
.▲
Исследовать сходимость ряда

Д Ряд
является геометрической прогрессией
со знаменателем q=x3/10.
Он
сходится, если |x3/10|
< 1, и расходится, если |x3/10|≥1-
Следовательно, промежуток сходимости
ряда определяется двойным неравенством
![]() .
Тот же результат можно получить, используя
формулы (2) и (3). ▲
.
Тот же результат можно получить, используя
формулы (2) и (3). ▲
362. Исследовать сходимость ряда

Δ Полагая х5 = t, получаем ряд
 (*)
(*)
Здесь ап = 2n/(2n—1), аn+1=2n+1/(2n+1). Находим радиус сходимости ряда (*):

Таким образом, ряд сходится, если |t| < 1/2.
Исследуем
сходимость ряда на концах промежутка.
Если t=1/2, то по
лучаем ряд
![]() .
Этот ряд расходится (его можно сравнить
.
Этот ряд расходится (его можно сравнить
с
рядом
![]() членами которого являются члены
гармонического
ряда, умноженные на 1/2). При t
= —1/2
получаем ряд
членами которого являются члены
гармонического
ряда, умноженные на 1/2). При t
= —1/2
получаем ряд
![]() Этот ряд сходится условно. Следовательно,
ряд (*) сходится,
Этот ряд сходится условно. Следовательно,
ряд (*) сходится,
если
—1,2≤t< 1/2. Таким образом, заданный ряд
сходится, если —1/2≤ x5
< 1/2, т. е. —![]() <х<
<х<
![]() .
Тот же результат можно получить, используя
формулу (2). ▲
.
Тот же результат можно получить, используя
формулу (2). ▲
363. Исследовать
сходимость ряда

∆В
данном случае имеем аn
= 0 при п=2k
— 1 и
 при п
= 2k. Для
отыскания радиуса сходимости удобнее
всего использовать формулу
(3). Находим
при п
= 2k. Для
отыскания радиуса сходимости удобнее
всего использовать формулу
(3). Находим
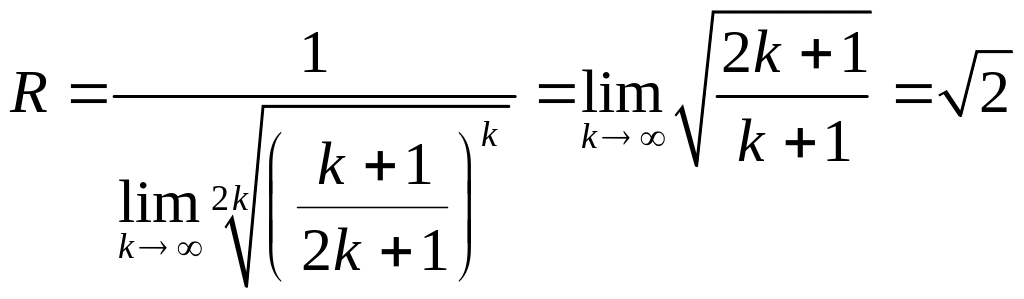 .
.
Исследуем
ряд на концах интервала сходимости.
Полагая х—2=![]() ,
получаем
числовой ряд
,
получаем
числовой ряд

Но
 Таким образом, при х—
2=
ряд
расходится.
То же самое имеет место и при х—2
= —
.
Итак,
область сходимости данного ряда 2—
< х < 2+
. ▲
Таким образом, при х—
2=
ряд
расходится.
То же самое имеет место и при х—2
= —
.
Итак,
область сходимости данного ряда 2—
< х < 2+
. ▲
364.
Исследовать
сходимость ряда
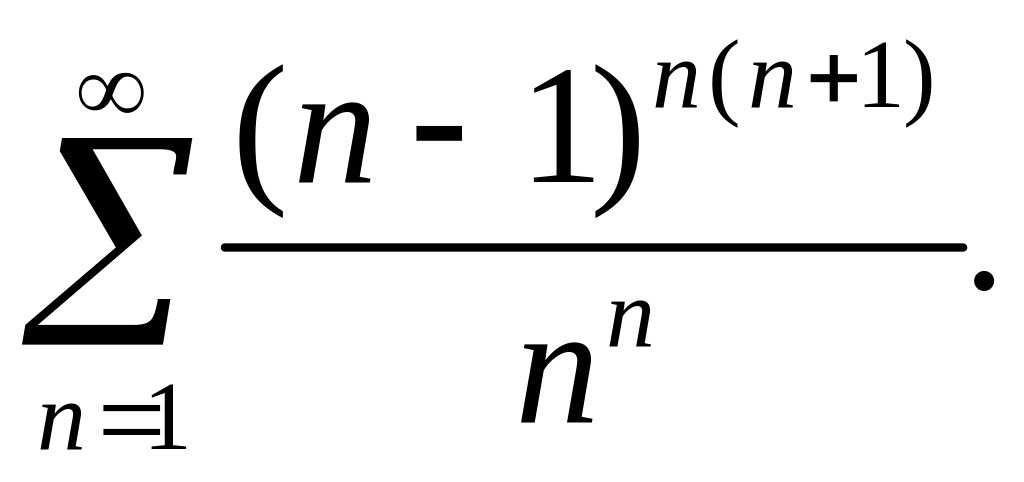
∆ Применяем
признак Коши, полагая
 .
Тогда
.
Тогда
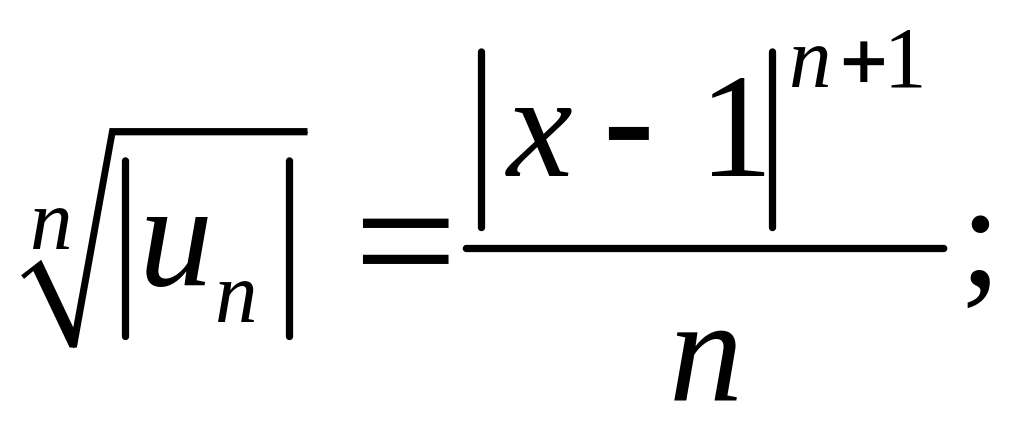
 .
.
Таким образом, ряд сходится, если |x— 1 |< 1, т. е. в промежутке 0≤x≤ 2. ▲
365. Исследовать
сходимость ряда
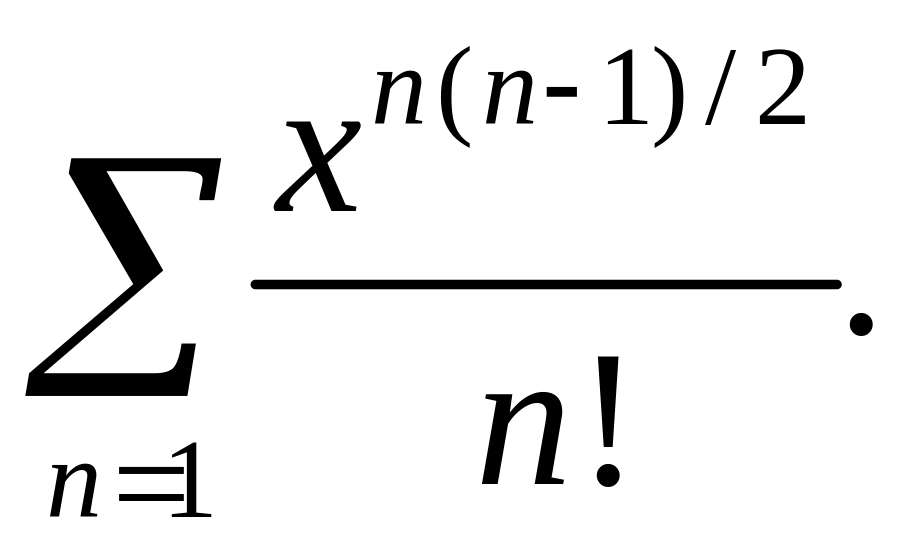
∆
Применяем признак
Даламбера, полагая
![]() ,
,![]() Тогда
Тогда

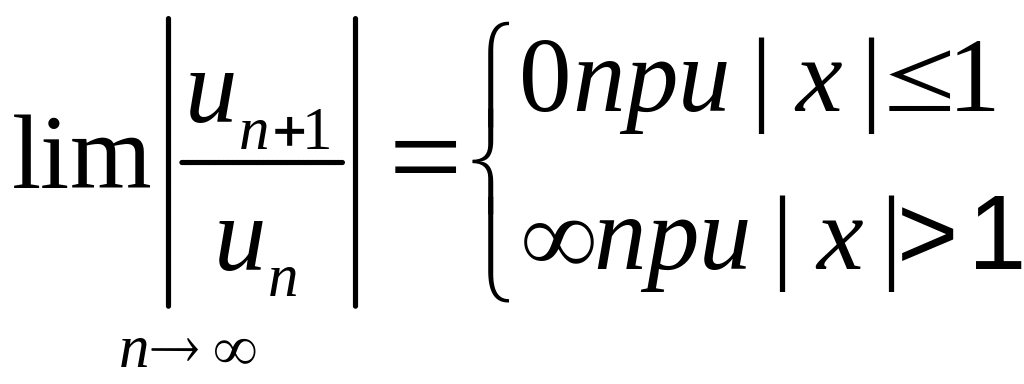
Итак, ряд сходится, если |x|<1, т. е. на отрезке -1≤x≤1
366. Найти сумму ряда 1 + 2х + Зх2+ ... + пхn-1+... (|x| < 1), продифференцировав почленно ряд 1 +х + х2+х3+ .. .+xn-1 + … (|x|<1).
∆
Воспользовавшись
формулой суммы членов бесконечно
убывающей геометрической
прогрессии
 ,
получаем
,
получаем
![]() .
.
Остается
продифференцировать полученное
равенство:
 ▲
▲
367. Найти
сумму ряда
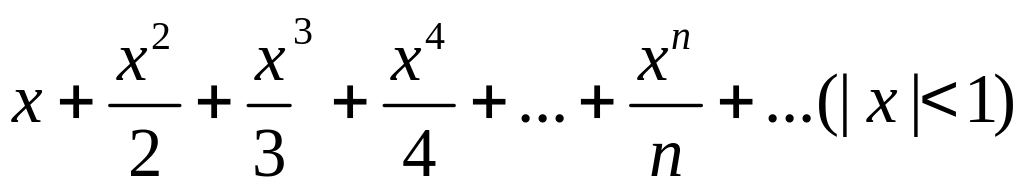
∆ Продифференцируем почленно заданный ряд и найдем его сумму по формуле , где а=1 и q=х; получим
.
Проинтегрировав затем в пределах от 0 до х, находим

Этот ряд сходится в промежутке [—1,1].▲
Исследовать сходимость степенных рядов:
368.

369.

370.

371.
![]()
372.

373.
 ●Положить
х2
=t.
●Положить
х2
=t.
374. 
375.

376.

377.
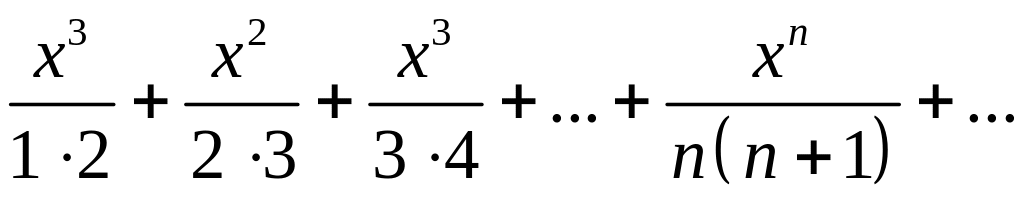
Найти суммы рядов:
378.  если
|x|<a.
если
|x|<a.
 ,если-a≤x<а.
,если-a≤x<а.
 если
|x|<a.
если
|x|<a. если |x|<1.
если |x|<1.
