2. Приведение системы сил к данному центру. Теорема Вариньона.

Согласно основной теореме статики центр приведения может быть выбран произвольно. Тогда для разных центров приведения, вообще говоря, получатся разные главный вектор и главный момент. Следовательно, возникает вопрос: как же на самом деле действует на тело исходная система сил?

Для ответа на этот вопрос следует выяснить, как изменяются главный вектор и главный момент при изменении центра приведения и ввести понятие инвариантов системы сил.

Совершенно очевидно, что главный вектор от выбора центра приведения не зависит: все силы переносятся параллельно самим себе, а затем складываются. Понятно, что результат будет одним и тем же.

Также очевидно, что главный момент зависит от выбора центра приведения. Возьмём новый центр О₁. Для одной силы будет:

Тогда

и

Следовательно, главный момент системы сил при изменении центра приведения будет преобразовываться по правилу:

Окончательно

1010\* MERGEFORMAT ()

Следует обратить внимание на то, что, если главный вектор равен нулю, , то согласно (10) будет

т.е. при главный момент системы не зависит от выбора центра приведения.

Скалярно умножим равенство (10) на главный вектор . Тогда

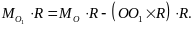
Учитывая, что

получаем

т.е. скалярное произведение главного вектора на главный момент не зависит от центра приведения.

Скалярные и векторные величины, не зависящие от выбора центра приведения, называются инвариантами системы сил.

Выше было установлено, что инвариантами системы сил являются:

главный вектор (3)

называемый первым инвариантом системы сил, и скалярное произведение главного вектора на главный момент

1111\* MERGEFORMAT ()

называемый вторым инвариантом системы сил.

Второй инвариант (11) системы сил может быть найден по формулам

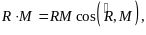1212\* MERGEFORMAT ()

или

1313\* MERGEFORMAT ()

В зависимости от значений 1-ого и 2-ого инвариантов система сил может быть приведена к одной из следующих простейших систем:

1. Одной силе (равнодействующей).

2. Паре сил.

3. Отсутствию сил (равновесию).

4. Динамическому винту.

Рассмотрим все возможности более подробно. Итак, пусть 2-ой инвариант равен нулю: . Это возможно в следующих случаях:

1)

2)

3)

4)

В случае 1) – равнодействующая , приложенная в центре О.

В случае 2) система приводится к паре сил с моментом , не зависящим от центра приведения (следствие из формулы (10)).

В случае 3) получаем равнодействующую, совпадающую с , но приложенную в точке О₁:

Наконец, в случае 4) получаем, что исходная система сил эквивалентна 0, т.е. на твёрдое тело как бы вообще не действуют никакие силы. Другими словами, получаем равновесие тела.

Равенства

являются векторными условиями равновесия любой системы сил.

Теперь рассмотрим случай, когда 2-ой инвариант не равен нулю: 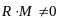. Это возможно, если

Рассмотрим сначала случай, когда

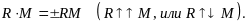
Такая система называется динамическим винтом.

Динамический винт – это совокупность силы и пары сил, момент которой лежит на одной линии с силой.

Эквивалентное определение: Динамический винт – это совокупность силы и пары сил, плоскость которой перпендикулярна к силе.

Если направление момента пары совпадает с направлением силы, динамический винт называют правым, если направления противоположны, то – левым.

Правый динамический винт.

Левый динамический винт.

Перейдём теперь к общему случаю

Докажем, что в этом случае система сил также эквивалентна динамическому винту. Разложим главный момент на две составляющих:

составляющую

1414\* MERGEFORMAT ()

и составляющую

1515\* MERGEFORMAT ()

Пара сил (15) от выбора центра приведения не зависит, ибо

т.е. выражается через инварианты системы сил.

С парой сил (14) поступим так же, как в случае .

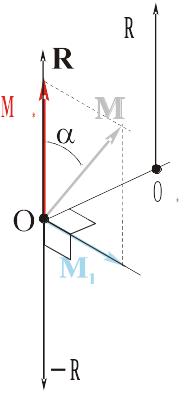
Таким образом, в точке О_*:

получим силу и пару сил, момент которой (так как он не зависит от центра приведения, его можно переместить в любую точку) направлен вдоль силы, т.е. динамический винт.

Все рассмотренные случаи можно свести в одну таблицу.

2-ой инвариант	1-ый инвариант	главный момент	Простейшая система сил
0		0	равнодействующая в центре О
	0		пара сил с моментом, не зависящим от центра О
			равнодействующая в центре О1:
	0	0	равновесие системы сил
			динамический винт

Теорема Вариньона. Если система сил имеет равнодействующую, то её момент относительно любого центра (или оси) равен сумме моментов всех сил системы относительно этого центра (или оси).

Доказательство. Пусть система сил имеет равнодействующую в центре О . Согласно равенству (10)

получаем в этом случае

Так как это момент равнодействующей относительно центра О₁, то теорема доказана.

Теорема Вариньона во многих случаях позволяет упростить вычисление моментов. Н а практике она чаще всего применяется в следующих ситуациях.

Пусть нужно вычислить момент относительно точки О силы , приложенной к стержню, изогнутому под прямым углом.

По определению алгебраического момента

и задача сводится к вычислению плеча h, которое в данной задаче находится не совсем просто.

Применим теорему Вариньона. Разложим силу на две составляющих: вертикальную и горизонтальную .

По аксиоме параллелограмма –равнодействующая сил : . Следовательно, по теореме Вариньона

но плечи для сил определяются очень просто

. Поэтому получим