Лекция 4

Понятие о сферическом и свободном движениях твёрдого тела.

Общие понятия сложного движения точки.

Вопросы лекции.

1. Понятие о движении тела с одной неподвижной точкой (сферическом движении).

2. Понятие о движении свободного твёрдого тела.

3. Общие понятия сложного движения точки.

1. Понятие о движении тела с одной неподвижной точкой (сферическом движении).

1.1 Общие понятия

Движение твёрдого тела с одной неподвижной точкой в определении не нуждается. Пусть точка О тела остаётся неподвижной: для .

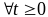Рассмотрим любые другие точки тела, не совпадающие с неподвижной, например, А, В, С.

Т.к. , то эти точки могут двигаться только по сферическим поверхностям с общим центром в неподвижной точке О и с радиусами, равными расстояниям от центра О до данной точки. Очевидно, что то же самое можно сказать и о любой другой точке этого тела.

Из этого факта происходит другое, не официальное, название движения твёрдого тела с одной неподвижной точкой: сферическое движение.

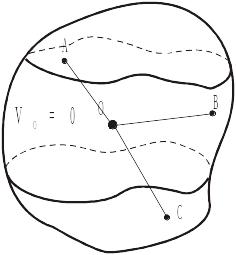
Итак, траектории всех точек тела при сферическом движении расположены на сферических поверхностях с общим центром в неподвижной точке. Но траектории могут быть весьма сложными кривыми. Примеры:

.

Можно доказать, что в движение тела представляет собой поворот на бесконечно малый угол вокруг оси, проходящей через неподвижную точку

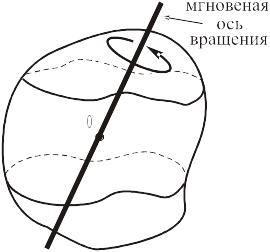
и называемой мгновенной осью вращения (М.О.В.).

При этом сама МОВ меняет положение в пространстве, поворачиваясь вокруг неподвижной точки. Таким образом, сферическое движение тела – это сумма двух вращений: тела вокруг МОВ и самой МОВ вокруг неподвижной точки.

Поскольку тело поворачивается вокруг МОВ, то его угловая скорость направлена вдоль мгновенной оси вращения

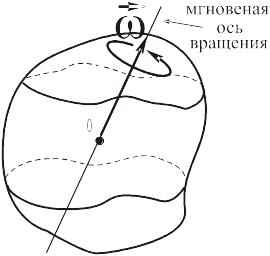
и называется мгновенной угловой скоростью тела.

Производная от мгновенной угловой скорости тела

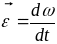11\* MERGEFORMAT ()

называется мгновенным угловым ускорением тела.

В отличие от вращательного движения тела вектор 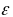мгновенного углового ускорения не направлен вдоль МОВ. Действительно, мгновенная ось вращения меняет своё положение в пространстве, всё время проходя через неподвижную точку тела, следовательно, – она описывает коническую поверхность

.

Мгновенная угловая скорость направлена вдоль МОВ, поэтому она также расположена на этой конической поверхности и, изменяясь по модулю, описывает на этой поверхности некоторую кривую (траекторию конца вектора 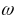, называемую годографом вектора)

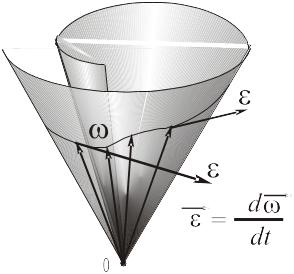
По аналогии с формулой для вектора скорости точки

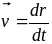
заключаем, что вектор мгновенного углового ускорения тела направлен по касательной к годографу мгновенной угловой скорости.

Вопрос о том, как практически определять векторы и будет рассмотрен позже.

2. Скорость и ускорение точки тела при сферическом движении

Т.к. в сферическое движение – это вращение вокруг МОВ, то

22\* MERGEFORMAT ()

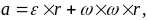33\* MERGEFORMAT ()

как при вращательном движении, но и – мгновенные угловая скорость и угловое ускорение соответственно.

Согласно (2) модуль скорости равен

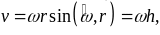44\* MERGEFORMAT ()

где расстояние от точки до МОВ.

Согласно (3) вектор ускорения точки тела равен сумме двух слагаемых:

55\* MERGEFORMAT ()

называемым вращательным ускорением точки, и

66\* MERGEFORMAT ()

называемым осестремительным ускорением точки.

Их модули находятся по формулам:

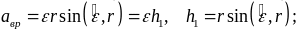77\* MERGEFORMAT ()

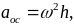88\* MERGEFORMAT ()

где h – то же, что и в формуле (4) для модуля скорости.

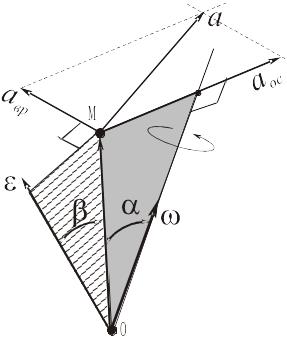
Формула (3) в силу введённых обозначений (5) и (6) может быть записана в виде

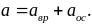99\* MERGEFORMAT ()

2. Углы Эйлера

Задавать сферическое движение тела можно различными способами. Одним из наиболее простых является задание движения с помощью углов Эйлера.

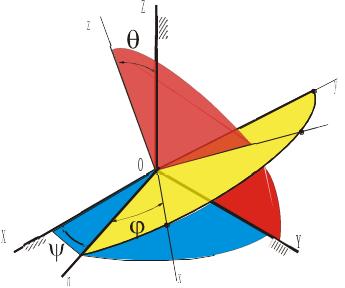
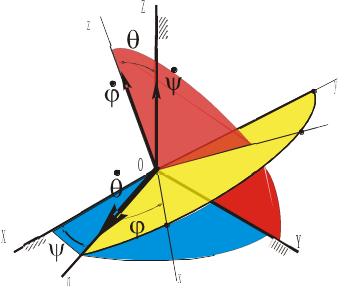
Система координат OXYZ – не подвижна в пространстве. Система Oxyz жестко связана с твёрдым телом и движется вместе с ним.

Линия пересечения n подвижной Oxy и неподвижной OXY плоскостей называется линией узлов (все названия взяты из астрономии).

Положение линии узлов в неподвижной плоскости можно определить углом 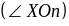 , который называется углом прецессии.

Величина наклона подвижной плоскости Oxy к неподвижной OXY задаётся углом  , называемым углом нутации.

Положение оси Ox (или Oy) в подвижной плоскости определяется углом  , называемым углом собственного вращения.

Три введенных угла ,  и  полностью определяют положение подвижных осей Oxyz относительно неподвижных OXYZ, а, следовательно,– и положение всех точек тела.

Если три угла Эйлера определить как функции от времени t, то положение тела будет известно в любой момент. Таким образом, функции

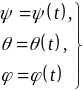1010\* MERGEFORMAT ()

задают закон сферического движения тела в углах Эйлера.

Если функции (10) известны, то можно вычислить производные. Тогда получим

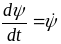1111\* MERGEFORMAT ()

угловую скорость прецессии;

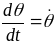1212\* MERGEFORMAT ()

угловую скорость нутации и

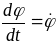1313\* MERGEFORMAT ()

угловую скорость собственного вращения. Векторы этих угловых скоростей показаны на рисунке.

Очевидно, что

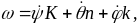1414\* MERGEFORMAT ()

где орты осей Z, n, z соответственно.

Равенство (14) проектируют на оси подвижной, или неподвижной, систем координат и находят вектор мгновенной угловой скорости тела по его проекциям на оси. Вычисляя производные от проекций мгновенной угловой скорости, находят проекции углового ускорения, а, следовательно, и сам вектор.