- •Сформулировать определение понятия производной.
- •III. Конкретизировать понятие производной (путём вычисления производной по определению: выяснение её геометрического смысла, графическое отыскание производной)
- •3) Мотивировать необходимость теорем о вычислении производной, сформулировать и доказать эти теоремы.
- •4) Рассмотреть приложение производной.
- •С помощью этой теоремы можно обосновать формулу Ньютона-Лейбница. Изучение доказательства проведем методом подготовительных задач.
- •Приращение аргумента, приращение функции.
- •Определение производной.
- •3. Понятие функции, непрерывной в точке.
- •1.1Роль аксиом в построении школьного курса геометрии.
- •1.2. Методика ознакомления учащихся с аксиомами в курсе.
- •I,. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
- •12. Через любые две точки можно провести прямую, и только одну.
- •47. Понятийный аппарат координатного метода. Методика обучения координатному методу
- •48. Методические особенности обучения математике в системе развивающего обучения д.Б. Эльконина - в.В. Давыдова
- •46 Метод схема изуч фор-ы объема прямоугольного параллелепипеда
№15.16 Методика введения понятий синуса, косинуса и тангенса на геометрическом материале. Основные тригонометрические тождества.
Знакомство с
тригонометрическим материалом начинается
в курсе геометрии при знакомстве с
прямоугольным треугольником. Понятия
![]() ,
,
![]() и
и
![]() острых углов треугольника вводится
для углов от
острых углов треугольника вводится
для углов от
![]() до
до
![]() ,
как отношение сторон этого треугольника.
Предварительно учащиеся должны усвоить
названия сторон прямоугольного
треугольника: катеты (стороны прямого
угла) и гипотенуза (сторона противолежащая
прямому углу). следующие выражения
«прилежащий» и «противолежащий»
,
как отношение сторон этого треугольника.
Предварительно учащиеся должны усвоить
названия сторон прямоугольного
треугольника: катеты (стороны прямого
угла) и гипотенуза (сторона противолежащая
прямому углу). следующие выражения
«прилежащий» и «противолежащий»
Первым вводится понятие угла и доказывается теорема: « Косинус угла зависит от градусной меры угла и не зависит от расположения и размеров треугольника».
С остальными
понятиями учащиеся знакомятся в пункте
« Соотношения между сторонами и углами
в прямоугольном треугольнике». 

Формируется свойство: синус и тангенс угла так же, как и косинус, зависят от величины угла.
Для синуса это доказывается так:
![]() =
=![]()
![]() ,
,
так как косинус зависит только от величины угла, то и синус зависит только от величины угла.
Из определений , и получаем следующие правила:
Катет, противолежащий углу
 ,
равен произведению гипотенузы на синус
;
,
равен произведению гипотенузы на синус
;Катет, прилежащий к углу , равен произведению гипотенузы на косинус ;
Катет, противолежащий углу , равен произведению второго катета на тангенс .
По этим правилам можно находить неизвестные элементы в прямоугольном треугольнике.
Вводятся основные тригонометрические тождества:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В частности, основное тригонометрическое тождество выводится из формулировки теоремы Пифагора:
![]() ,
,
![]() .
.
Учащиеся
знакомятся с некоторыми свойствами
функций острого угла: 1) при возрастании
острого угла
и
![]() возрастают, а
возрастают, а
![]() -
убывает; 2) для любого острого угла
:
-
убывает; 2) для любого острого угла
:
![]() ,
,
![]() ;
которые формулируются как теоремы. Их
доказательство связывается с соотношениями
острых углов в прямоугольном треугольнике:
;
которые формулируются как теоремы. Их
доказательство связывается с соотношениями
острых углов в прямоугольном треугольнике:
![]() ,
,
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
.
![]() ,
тогда из равенства правых частей
получаем:
.
,
тогда из равенства правых частей
получаем:
.
![]() ,
тогда
.
,
тогда
.
№17.
Методика введения определений
тригонометрических функций углов от
до
![]() .
.
Расширение области определения тригонометрических функций от до происходит в теме: «Декартовы координаты на плоскости».
Рассмотрим
окружность с центром в начале координат
произвольного радиуса R.
Откладываем в полуплоскость
![]() угол
угол
![]() .
Пусть точка
.
Пусть точка
![]() имеет координаты
имеет координаты
![]() и
и
![]() .
.
![]()
![]() ,
,
![]() ,
то из треугольника
,
то из треугольника
![]() :
:
![]() ,
,
![]() .
.
![]()
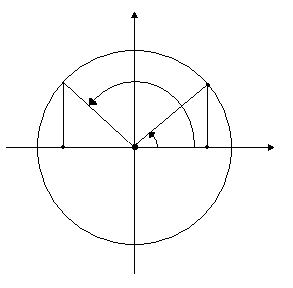 Определяются
значения
Определяются
значения
![]() и
этими формулами для любого угла α (для
и
этими формулами для любого угла α (для
![]() 0-исключается).
Можно найти значения этих функций для
углов 900,
00,
1800.
Доказывается, что для любого угла α
, 00<α<1800,
0-исключается).
Можно найти значения этих функций для
углов 900,
00,
1800.
Доказывается, что для любого угла α
, 00<α<1800,
![]()
![]() .
.
y![]() п
п![]()
А1(x1, y1)
1800-α
A(x, y)![]()
x
B
B1
α
R
O![]()
![]()
Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности.
Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 00 до 1800; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
№18. Методика изучения тригонометрических функций в курсе алгебры и начала анализа.
Традиционная методическая схема изучения тригонометрических функций:
в начале определяются тригонометрические функции для острого угла прямоугольного треугольника;
затем введенные понятия обобщаются для углов от
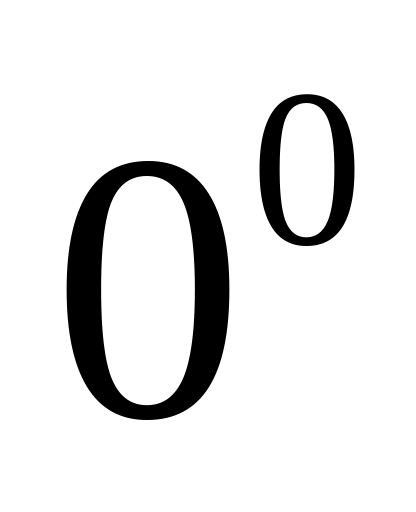 до
до
 ;
;тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
В курсе алгебры и начала анализа осуществляется заключительный этап изучения, который включает:
Закрепление представлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот;
Формирование представлений об углах с градусной мерой, большей
 ;
формирование представлений об углах
с положительной и отрицательной
градусными мерами; перевод этих градусных
мер в радианы (положительные и
отрицательные действительные числа);
;
формирование представлений об углах
с положительной и отрицательной
градусными мерами; перевод этих градусных
мер в радианы (положительные и
отрицательные действительные числа);Описание тригонометрических функций на языке радианной меры угла;
Утверждение функциональной точки зрения на
 ,
,
 ,
и
(трактовка
,
,
и
как функций действительного аргумента,
установление области определения,
области значений, построение графика
функции, установление промежутков
монотонности, знакопостоянства и т.д.);
,
и
(трактовка
,
,
и
как функций действительного аргумента,
установление области определения,
области значений, построение графика
функции, установление промежутков
монотонности, знакопостоянства и т.д.);Повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом которых является тождество
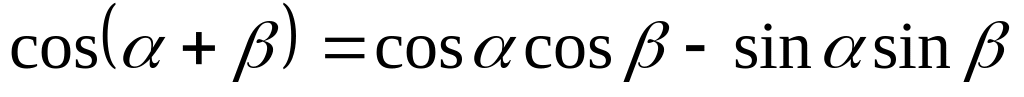 ;
;
Применение тригонометрических тождеств в тождественных преобразованиях и при решении задач по стереометрии.
В курсе «Алгебра
9» учащиеся знакомятся с функциональной
точкой зрения. Выражения
и
определимы
при
![]() ,
т.к
,
т.к
![]() угла поворота можно найти соответствующее
значение дробей
угла поворота можно найти соответствующее
значение дробей
![]() и
и
![]() . Выражение
имеет смысл при
,
кроме углов поворота
. Выражение
имеет смысл при
,
кроме углов поворота
![]() ,
,
![]() ,
…, т.к. имеет смысл дробь
,
…, т.к. имеет смысл дробь
![]() .
.
Каждому допустимому
значению
![]() соответствует единственное значение
,
,
и
соответствует единственное значение
,
,
и
![]() .
Поэтому
,
,
и
.
Поэтому
,
,
и
![]() являются функциями угла
.
Их называют тригонометрическими
функциями.
являются функциями угла
.
Их называют тригонометрическими
функциями.
Учащиеся знакомятся со следующими общефункциональными свойствами этих функций:
область значения и -
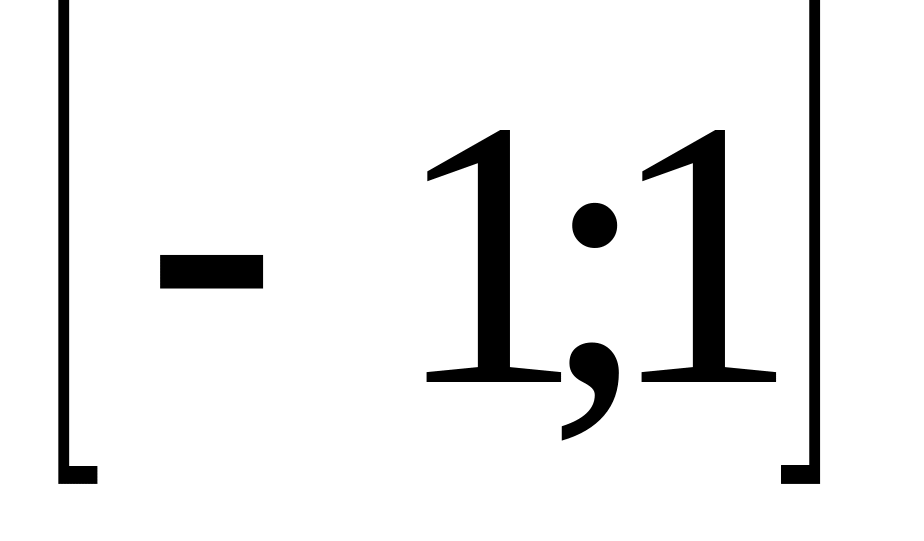 ,
для
и
-
множество всех действительных чисел.2)
промежутки знакопостоянства:
,
для
и
-
множество всех действительных чисел.2)
промежутки знакопостоянства:
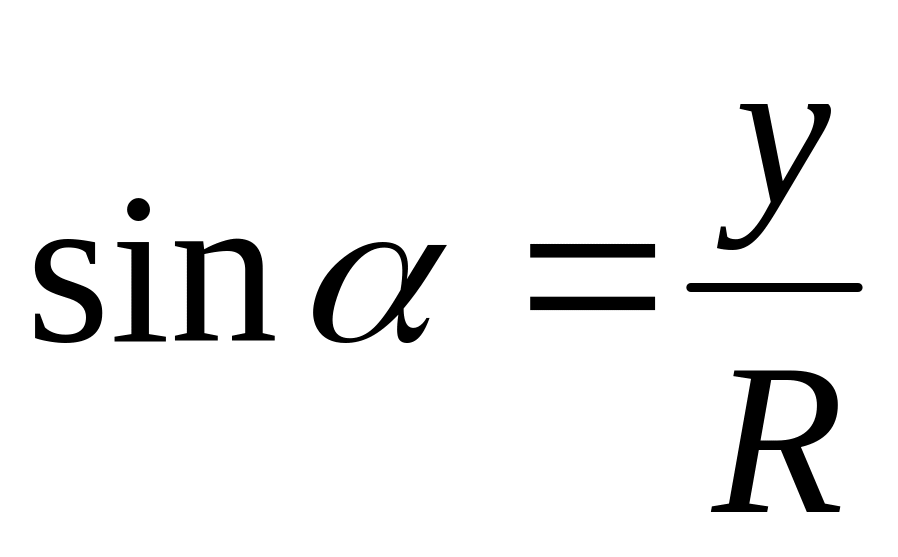 ,
то значит
зависит от знака
и т.д. 3)
,
и
являются нечетными функциями, а
является четной функцией. 4) при изменении
угла на целое число оборотов значение
,
,
,
не изменится (под обратным понимаем
поворот на
).
,
то значит
зависит от знака
и т.д. 3)
,
и
являются нечетными функциями, а
является четной функцией. 4) при изменении
угла на целое число оборотов значение
,
,
,
не изменится (под обратным понимаем
поворот на
).
Определение тригонометрической функции выглядит так:
Окружность радиуса 1 с центром в начале координат называют единичной
окружностью.
Пусть точка
![]() единичной окружности получена при
повороте точки
единичной окружности получена при
повороте точки
![]() на угол в
радиан. Ордината точки
- это синус угла
.
Числовая
функция,
заданная формулой
на угол в
радиан. Ордината точки
- это синус угла
.
Числовая
функция,
заданная формулой
![]() ,
называется синусом числа, каждому числу
ставится в соответствие число
,
называется синусом числа, каждому числу
ставится в соответствие число
![]() .
.
№21. Образовательные цели изучения производной функции.
Цель изучения курса алгебры и начала анализа в 10-11 в.в. систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовки необходимого апорта для изучения геометрии и физики.
Курс характеризуется содержательным раскрытием понятий, утверждений и методов.
При изучении темы «Производная» проявляются известные трудности, связанные с осуществлением предельных переходов. Важно поэтому придать изложению возможно более наглядный и конкретный характер.
Включённые в курс сведения о пределах имеют вспомогательный характер, они необходимы для вывода формул производных. Основное внимание должно быть уделено не формальному применению теорем о пределах, а сознательному проведению предельных переходов для приближённого вычисления значений конкретных функций и их приращений. Многочлены невысоких степеней и их частных -наиболее простой объект для иллюстрации идеи предельного перехода.
Определению производной функции как предела разностного отношения предшествует рассмотрению особенностей поведения графиков гладких функций, приводящее к понятию касательной. Производная функции появляется сначала как тангенс угла наклона касательной к оси абсцисс. Тем самым с понятием производной на первом этапе связывается наглядный образ – касательная. Предельные переходы появляются как средство вычисления производной.
При изучении применения производной существенная роль отводится наглядным представлениям о производной. Опора на геометрический и механический смысл делают интуитивно ясными критерии возрастания и убывания функций, признаки максимума минимума.
Решение тестовых задач физического, геометрического и практического содержания с применением производной позволяет учащимся ознакомиться со всеми этапами решения прикладных задач: составление математической модели (перевод задачи на язык функций), решение полученной задачи средствами математического анализа, и наконец, интерпретация полученного решения в терминах исходной задачи.
№22. Методическая схема изучения производной.
Привести подводящую задачу, раскрывающую физический смысл понятия производной: свободное падение тела, которое не является равномерным. Охарактеризуем скорость падения в каждый данный момент времени t , т.е. введём понятие мгновенной скорости свободного падения тела. Известно, что средняя скорость определяется отношением
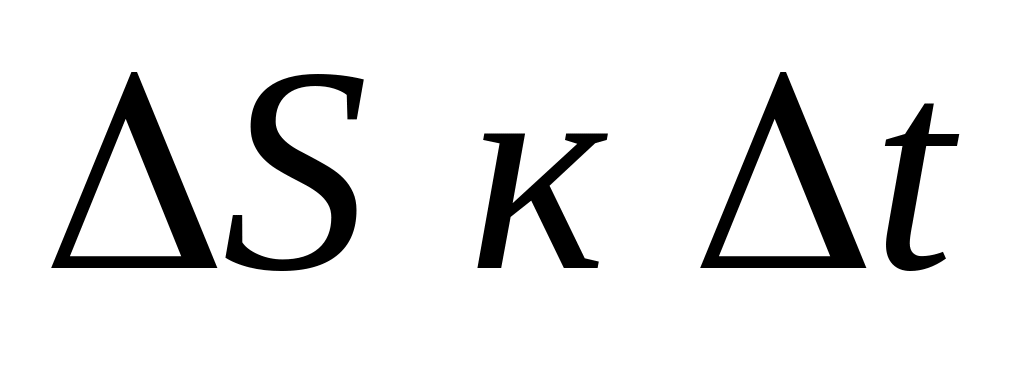 ,
причём чем меньше значение
,
причём чем меньше значение
 ,
тем менее «заметно» изменение средней
скорости падения. При
,
тем менее «заметно» изменение средней
скорости падения. При
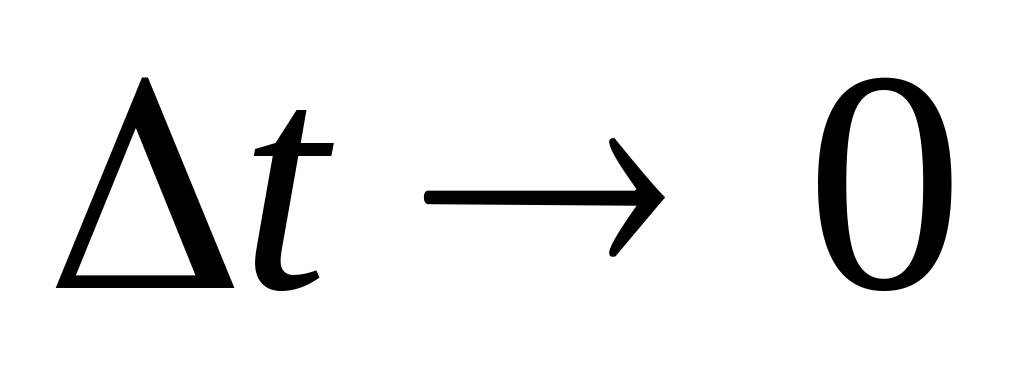 ,
отношение
,
отношение
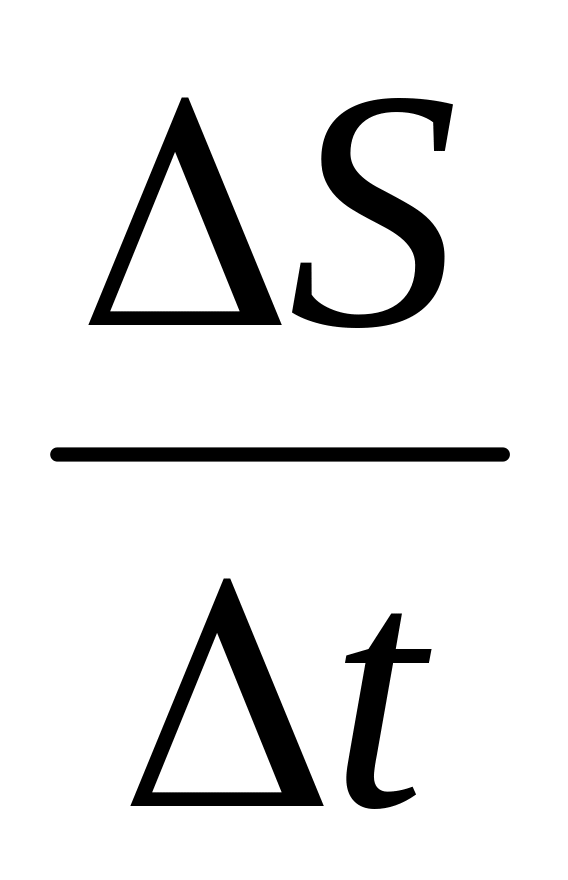 стремится к значению мгновенной
скорости. Таким образом мгновенная
скорость характеризует скорость
изменения пути
стремится к значению мгновенной
скорости. Таким образом мгновенная
скорость характеризует скорость
изменения пути
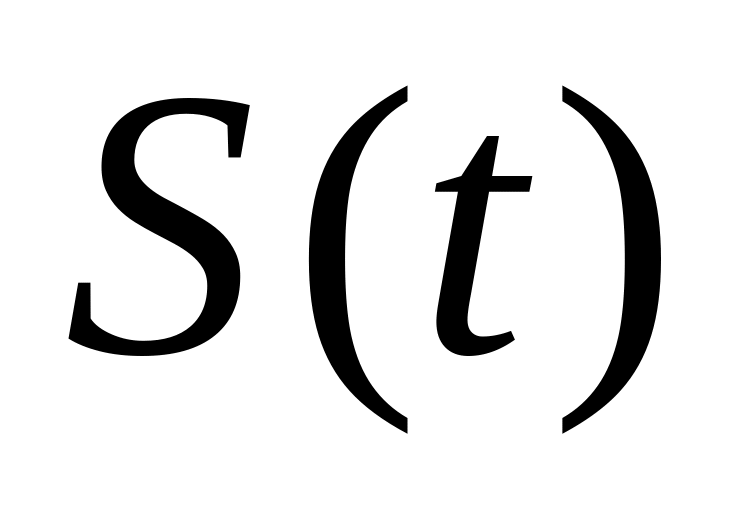 в
момент времени t.
в
момент времени t.
В общем случае, с любым реальным процессом может быть связана задача:
Пусть
![]() -параметр
данного процесса, зависимости от x
; найти скорость изменения параметра
в момент, когда
-параметр
данного процесса, зависимости от x
; найти скорость изменения параметра
в момент, когда
![]() .
Решение задачи сводится к нахождению
отношения приращения параметра
.
Решение задачи сводится к нахождению
отношения приращения параметра
![]() ,
соответствующую приращению
,
соответствующую приращению
![]() .
.
Сформулировать определение понятия производной.
Так как в определении отсутствует понятие предела, то первоначально следует сформировать у учащихся понятие приращения как изменения и аргумента и функции.
Например:
![]()
После рассмотрения геометрического смысла производной вводим определение:
Производной
функции в точке
![]() называется число, к которому стремится
разностное отношение:
называется число, к которому стремится
разностное отношение:
![]()
Полезен небольшой
анализ формулировки определения,
позволяющий чётче выделить признаки
данного понятия: 1) число, 2) к которому
стремится разностное отношение
![]()
при
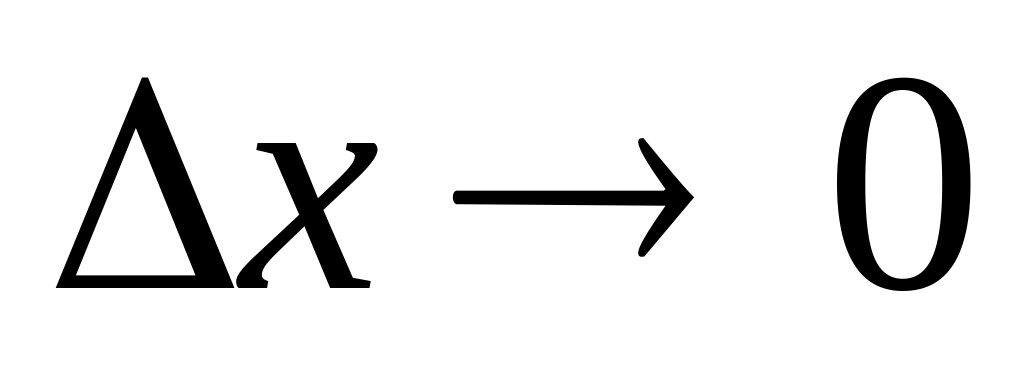
Закреплению
определения производной способствует
вопрос: «Как найти производную функции
в точке
?»,
ответ на который может быть дан в форме
алгоритма: 1) значению
придаём
приращение
![]() ;
2) находим приращение функции
в точке
;
2) находим приращение функции
в точке
![]() ;
3) составляем разностное соотношение;
4) находим число
;
3) составляем разностное соотношение;
4) находим число
![]() (если
такое число существует), к которому
стремится
при
(если
такое число существует), к которому
стремится
при
III. Конкретизировать понятие производной (путём вычисления производной по определению: выяснение её геометрического смысла, графическое отыскание производной)
3) Мотивировать необходимость теорем о вычислении производной, сформулировать и доказать эти теоремы.
4) Рассмотреть приложение производной.
№23. Методическая схема изучения первообразной функции.
В школьном учебнике были “испытаны” различные варианты введения понятия интеграла. В первых изданиях учебного пособия (под ред. А.Н. Колмогорова) интеграл определяется с помощью формулы Ньютона-Лейбница (как приращение первообразной), в более поздних изданиях применялось традиционное определение интеграла как предела интегральных сумм.
Методическая схема изучения первообразной:
рассмотреть примеры взаимно обратных операций;
ввести интегрирование как операцию, обратную дифференцированию, а первообразную как результат операции интегрирования;
выполнить упражнения типа: “Доказать, что данная функция
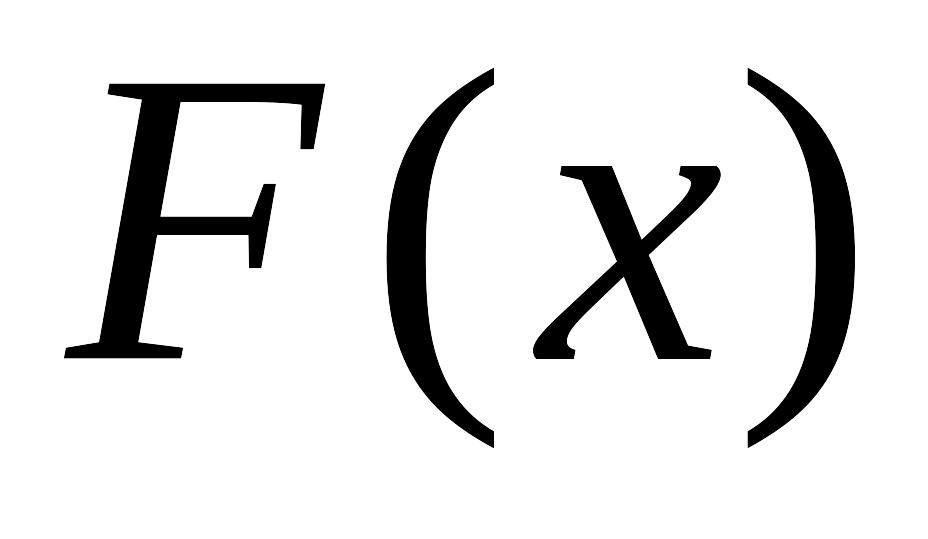 есть первообразная другой данной
функции
есть первообразная другой данной
функции
 ”,
“Решить задачи на отыскание первообразной
для данной функции
”;
”,
“Решить задачи на отыскание первообразной
для данной функции
”;ознакомить учащихся с основным свойством первообразной;
составить таблицу первообразных;
ознакомить учащихся с правилами нахождения первообразных;
решить физические задачи с применением первообразной.
При введении
понятия первообразной пользуются
аналогией с известными учащимся примерами
взаимно обратных операций.
Например, операция сложения позволяет
по двум данным числам найти третье число
– их сумму. Если же известно первое
слагаемое и сумма, то второе слагаемое
может быть “восстановлено” выполнением
операции вычитания. Следовательно,
вычитание – операция, обратная сложению,
приводящая к единственному результату.
Однако такое бывает не всегда. Например,
возведение в квадрат числа 3 дает число
9. Пусть теперь известно, что число 9
является квадратом некоторого числа:
![]() .
Выполнив обратную операцию – извлечение
квадратного корня – получаем два
значения: 3 и -3.
.
Выполнив обратную операцию – извлечение
квадратного корня – получаем два
значения: 3 и -3.
Дифференцирование
функции
![]() приводит к новой функции
приводит к новой функции
![]() ,
которая является производной функции
Пусть теперь известно, что производная
некоторой функции
,
которая является производной функции
Пусть теперь известно, что производная
некоторой функции
![]() равна
равна
![]() ,
т.е.:
,
т.е.:![]() ;
требуется найти функцию
.
;
требуется найти функцию
.
Операция
нахождения функции
по ее производной
![]() называется интегрированием.
Таким образом, интегрирование является
операцией, обратной дифференцированию;
результат операции интегрирования
называется первообразной.
После
этого сообщается определение первообразной:
функция
называется первообразной для функции
f(x)
на заданном промежутке, если для всех
x
из этого
называется интегрированием.
Таким образом, интегрирование является
операцией, обратной дифференцированию;
результат операции интегрирования
называется первообразной.
После
этого сообщается определение первообразной:
функция
называется первообразной для функции
f(x)
на заданном промежутке, если для всех
x
из этого
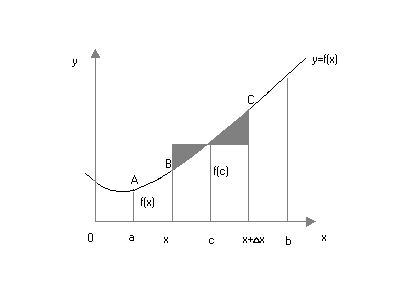
№24. Метод схема изуч теоремы о площади криволинейной трапеции
Центральное место в изучении этой темы является теорема о площади криволинейной трапеции: “Пусть f – непрерывная и неотрицательная на отрезке [a, b] функция, S – площадь соответствующей криволинейной трапеции. Если F есть первообразная для f на отрезке [a, b], то S=F(b)-F(a).”