
Билет № 1
1. Задачи и содержание курса. Связь курса с другими дисциплинами.
Измерения составляют основное содержание всех видов маркшейдерских и геодезических работ, связанных с получением количественных характеристик изучаемых объектов. Качество выполненных измерений характеризуется их точностью. Теория математической обработки измерений разрабатывает рациональные приемы и методы обработки результатов измерений и оценки их точности. Все величины, используемые в маркшейдерско-геодезической практике, можно разделить на измеренные и вычисленные При этом измерением называется процесс сравнение определяемой величины с однородной ей величиной, принятой за единицу измерения. Результат измерения выражается равенством
l = n·l˳,
где l˳ – единица измерения;
n – отношение измеряемой величины к единице измерения.
На качество результатов измерений влияют погрешности исполнителя, прибора и внешних условий. По точности результаты измерений делят на равноточные и неравноточные. Равноточными измерениями называются однородные результаты, полученные при измерениях искомой величины в одинаковых условиях (инструмент, метод измерения, число приемов, квалификация наблюдателя, внешние условия). При несоблюдении этих условий результаты измерений называются неравноточными. При обработке все измерения, по сути, приводятся к равноточным путем введения соответствующих коэффициентов - весов. Влияние таких измерений на результаты вычислений оказывается одинаковым. В теории математической обработки измерений важное значение имеют понятия необходимых и избыточных измеренных величин. Для решения любой геодезической задачи на местности необходимо измерить некоторое минимальное число величин. Эти величины и называют необходимыми. Их количество называют числом необходимых величин. Например, для определения всех сторон и углов плоского треугольника необходимо измерить три независимые его элемента: любую сторону и любые два угла или три стороны.
Разность числа всех измеренных и числа необходимых величин называют числом избыточных величин. Например, если в плоском треугольнике измерены три угла и одна сторона, то одно измерение избыточное.
В геодезической практике избыточные измеренные величины обязательны. Они дают возможность обнаружить промахи в измерениях и в вычислениях и повышают точность определения искомых величин. Проблема математической обработки измерений возникает из-за наличия избыточных измерений величин и погрешностей измерений. Действительно, при отсутствии избыточных измерений искомые величины вычисляются по четким математическим зависимостям. Например, плоский треугольник решается по теореме синусов или косинусов. Такие расчеты бесконтрольны, возможны грубые ошибки, которые не исключаются при обработке, невозможно оценить точность измеренных и вычисленных величин. При решении большинства геодезических и маркшейдерских задач это недопустимо.
Таким образом, математическая обработка измерений сводится к определению вероятнейших значений измеренных величин, их функций и оценке точности результатов измерений и искомых величин.
Основные задачи математической обработки:
1. изучение законов возникновения и распределения погрешностей измерений и вычислений;
2. установление критериев для обнаружения в результатах измерений систематических погрешностей и промахов;
3. определение вероятнейших значений измеряемых величин по результатам их многократных измерений;
4. предрасчет ожидаемой точности и оценка точности полученных результатов измерений;
5. характеристика точности окончательных значений измеренных величин по результатам математической обработки измерений;
6. установление силы и формы связи между измерениями и их погрешностями.
Дисциплина “Математическая обработка маркшейдерско-геодезических измерений” включает в себя: теорию погрешностей измерений и метод наименьших квадратов. При этом теория погрешностей измерений основана на использовании понятий теории вероятностей и элементов математической статистики. Теория погрешностей измерений рассматривает вопросы обработки многократных измерений одной величины, ряда многократных двойных измерений, функций измеренных величин, интерполирование и аппроксимация измеренных значений функций.
На втором курсе мы только изучаем первую часть дисциплины,включающую пять разделов; основные понятия,положения и теоремы теории вероятностей,случайные величины,свойства и законы их распределения,элементы математической ствтистики,основы теории погрешностей измерений,математическая обработка измерений одной величины. Выполняем две контрольные работы. Теория математической обработки непосредственно связана с математикой,геодезией, картографией, географией и тд.
2. Оценка точности результатов измерений по невязкам.
(Оценка точности функций величин, полученных в результате коррелированных и некоррелированных измерений) (справочник геодезиста т.1 стр. 42)В инженерной практике часто возникают задачи, когда интересующая наблюдателя величину непосредственно измерить нельзя. В таких случаях приходит с измерить некоторые величины (аргументы), связанные с искомой величиной функцией, а искомую величину вычислять.
Дана функция
![]()
Где X1, X2, …, Xn – попарно коллерированные аргументы, полученные из измерений со средними квадратическими ошибками mu вычисляются по формуле
![]()
Значения производных вычисляются, по приблизительным значениям аргументов, но приблизительно к истинным значениям. От степени этой близости зависит точность формулы. Она является точной только для линейных функций.
При вычислениях согласно формулы в результате следует получать не болие двух значащих цифр. Сл., значения производных сл. Вычислять не болие чем с тремя значащими цифрами. Знание точных значений аргументов Хi обычно не требуется.
Билет 2. Вопрос 1 Историческое развитие математической обработки геодезических измерений связано с именами таких великих ученых, как К. Гаусс, Ф. Гельмерт, Л. Крюгер, П. Лапласс, А.Лежандр. Научные традиции Гаусса в России продолжили А.П. Болотов, А.Н. Савич, И.И. Померанцев, В.В. Витков-ский и другие. Значительный вклад в развитие теоретического фундамента внесли такие видные ученые-геодезисты, как В.Д. Большаков, П.А. Гайдаев, В.Н. Ганьшин, В.Г. Зданович, А.А. Изотов, Ф.Н. Красовский, Н.Г. Келль, Ю.В. Лин-ник, А.И. Мазмишвили, М.С. Молоденский, В.В. Попов, К.Л. Проворов, Н.А. Урмаев, А.С. Чеботарев и другие. Современное развитие науки и техники обеспечивает новые возможности решения задач геодезии и создает предпосылки к разработке новых методов их решения, применительно к современным измерительным технологиям и средствам вычислений. Это позволяет выполнять математическую обработку измерений, реализующую не только классические методы, но и другие, основанные на теории исследования операций. Такой подход расширяет возможности практического использования вероятно-статистических методов математической обработки наблюдений, в наибольшей степени учитывающих разнообразие информации о характере формирования погрешностей измерений.
В связи с этим возрастает актуальность разработки путей реализации теоретических основ путем разработки алгоритмов и программ, обеспечивающих эффективное применение компьютерных технологий обработки различных по виду и точности геодезических измерений.
Вопрос 2. По условиям измерения различают равноточные и неравноточные измерения. Если измерения какой-либо физической величины выполняются одинаковыми по точности приборами в одних и тех же условиях с одинаковой тщательностью, такие измерения считаются равноточными.
В большинстве
случаев при обработке прямых равноточных
измерений исходят из предположения
нормального закона результатов и
погрешностей измерений. По результатам
серии снятия отсчетов по формуле
 вычисляется
наилучшая оценка математического
ожидания (среднее арифметическое).
вычисляется
наилучшая оценка математического
ожидания (среднее арифметическое).
Если известна
систематическая погрешность и она
постоянна, то ее исключают из найденной
величины математического ожидания. По
формуле
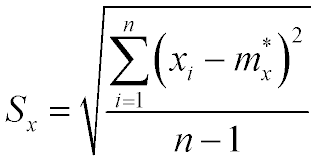
определяется наилучшая оценка СКО Sx (статистическая). Помимо значений mx и Sx как точечных оценок при обработке результатов прямых равноточных измерений пользуются также интервальными оценками. Задав значение доверительной вероятности tx (из ряда 0,90, 0,95, 0,99), результат измерений записывают в виде

№ 3 ПОНЯТИЕ ОБ ИЗМЕРЕНИЯХ И ИХ ОШИБКАХ
измерения-это процесс сравнения измеряемой величины с величиной принятой за единицу сравнения, в результате которого получается именованная число, называемое результатом измерения. различают: прямые, или непосредственные и косвенные измерения. непосредственными наз. такие измерения. когда определяемые величины получают прямо из измерений, в результате непосредственного сравнения их с единицей измерений. примеры непосредственных измерений-определение расстояний мерной лентой, измерение угла теодолитом. косвенными явл. такие измерения, при которых определяемые величины получают как функции непосредственно измеренных величин. косвенный метод предполагает вычисления значения искомой величины. например, превышение при тригонометрическом нивелировании явл. функцией расстояния и угла наклона, измеренных непосредственно на местности. результаты измерений разделяют на равноточные и неравноточные. равноточными наз. результаты измерения однородных величин, получ. при многократных измерениях в сходных условиях(одним наблюдателем и тем же прибором, одним методом и при одних и тех же условиях окр. среды). при нарушении даже одного из перечисленных условий р-ты измерений относят к неравноточным. при матем-кой обработке результатов топографо-геодезических измерений определенное значение имеют понятие о необходимом и избыточном числе измерений. в общем случае для решения любой топографической задаче необходимо измерить некоторое минимальное число величин, обеспеч. решение задачи. эти измерения наз. числом необходимых измерений t. разность k при вычитании числа необходимых измерений t из числа всех измерений величин n, наз. числом избыточных величин k=n-t. избыточные измерения величины позволяют обнаружить ошибки в результатах измерений и вычислений и повысить точность определяемых величин. ошибки бывают: приборные, личные, внешние, методические. измерения считают правильными если ошибки по величине не превышают допуск, который указан в нормативной литературе. ошибки измерений превышают- они сопровождаются грубыми измерениями. для их устранения предусмотрены контрольные измерения. истинная ошибка разделена на две составляющие: случайная и систематическая.
Билет 4
Случайной называется величина, которая в результате опыта может принять то или иное одно значение, причем неизвестно заранее, какое именно. Случайные величины могут быть: Прерывными (дискретными) - случайная величина, возможные значения которой можно заранее указать (Например, число попаданий при трех выстрелах — 0, 1, 2, 3;). Непрерывными - случайная величина, которая может принять любые значения на некотором непрерывном интервале, которые не могут быть перечислены заранее(напримеррезультат измерения какой-либо величины, координаты точек попадания при стрельбе). Для полной характеристики случайной величины недостаточно знать ее значения, а необходимо также знать вероятности, соответствующие этим значениям, т. е. ρ 1, р2, р3, . . . , рn, или ожидаемые относительные частоты (статистические вероятности) этих значений. Закон распределения случайной величины-всякое соотношение, при помощи которого устанавливаетсясвязь между значениями случайной величины и соответствующими им вероятностями. Он может быть задан:
1.Аналитически
в виде формулы
xi
x1
x2
….
xn
pi
p1
p2
….
pn
3 Для задания закона распределения как прерывной, так и непрерывной случайной величины служит так называемая функция распределения. Функцией распределения называется вероятность того,что случайная величина принимает значение, меньшее некоторого заданного значения х случайной величины X, т. е. Р(х) = Р(Х<х). Свойства функцииР(х):
1)
F(-
Получив в результате многократных неравноточных наблюдений одной и той же величины ряд x1, x2, …xn с весами p1, p2…..pnвычисляют:
1.Общую
арифметическую средину (весовая
средняя)
2.Вычисляют
уклонения
где
ошибка округления при вычислении х
будет
3.
Вычисляют
4.
Вычисляют ошибки: среднююквадратическую
ошибку единицы веса
|
||||||||||
Билет 13
Иногда применяют принцип пренебрегаемого (ничтожного) влияния отдельных источников ошибок, т. е. измерения проектируют таким образом, чтобы отдельные процессы выполнялись гораздо точнее, чем это необходимо по расчетам, и при определении суммарной ошибки влиянием этих источников пренебрегают.
Рассчитаем
для выражения
Примем
Чтобы
влияние источника σ1
не превышало средней квадратической
ошибки определения σ, необходимо,
чтобыК=2 (при точности определения
На практике этот принцип применяют при разбивочных работах.
2.Предмет и задачи теории ошибок. При осуществлении наблюдений исследуемых объектов наблюдатель обычно получает ряд значений некоторых физических величин, которые затем используются при расчетах, проектировании и т. д. Следует отметить, что наблюдатель при этом ставит передсобой задачу получить указанные значения физических величин с возможно большей точностью или, иначе говоря, с возможно меньшей ошибкой. Однако понятия «возможно большая точность», «возможно меньшая ошибка» неконкретны, так как не сопровождены числовыми характеристиками. Очевидно, при числовой характеристике ошибки, равной нулю, наблюдения следует считать выполненными безошибочно (идеальный случай). Вместе с тем опыт свидетельствует, что безошибочных наблюдений не бывает, какими бы точными приборами они ни производились. Совершенствование приборов и методики работ, выбор наилучших условий наблюдений могут привести к повышению точности, т. е. к уменьшению отклонений полученных значений наблюденной величины от ее точного (истинного) значения. Вопрос, следовательно, сводится к определению порядка величин ошибок, ожидаемых при данных условиях наблюдений. Предполагается, что определяемая величинав процессе наблюдений остается постоянной. Если наблюдают переменную величину, то результат наблюдения должен быть отнесен к точно обозначенному моменту времени. Причины возникновения ошибок наблюдений весьма разнообразны и зависят от точности приборов, внешних условий, при которых производятся наблюдения, от опытности наблюдателя, от характера определяемых физических величин н т. д. В теории ошибок изучают причины возникновения и законы распределения ошибок наблюдений, а также свойства различных видов ошибок и разрабатывают методику наблюдений, позволяющую удержать эти ошибки в заданных пределах.
3.
|
Билет №5 1.Функция распределения.
Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х: F (x) = p (X < x). Свойства функции распределения. 1) 0 ≤ F(x) ≤ 1. Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность. 2) Функция распределения является неубывающей функцией, то есть F(x2) ≥ F(x1) при х2 > x1. Это следует из того, что F(x2) = p(X < x2) = p(X < x1) + p(x1 ≤ X < x2) ≥ F(x1). 3) В частности, если все возможные значения Х лежат на интервале [a, b], то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное. 4) Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала: p ( a < X < b ) = F(b) – F(a). Справедливость этого утверждения следует из определения функции распределения (см. свойство 2). Для дискретной случайной величины значение F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции. График функции распределения имеет ступенчатый вид:
|
Билет №6 1 Плотность распределения Наглядное представление о характеристике распределения в окрестности различных точек дается функцией которая называется плотность распределения вероятности или дифференциальным законом. Плотность распределения случайной величины в точке х называется предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+Δх к длине этого участка Δх Плотность распределения – это производная от функции распределения. Свойства f(x)≥0 Несобственный интеграл от плотности вероятности в бесконечных пределах равен 1. Плотность заключенная под кривой всегда равна 1. Вероятность попадания случайной величины Х на участке от а до b равна интегралу от плотности распределения взятому по этому участку.
2 Свойства арифметической средины. Если результаты измерений свободны от систематических ошибок, то арифметическая средина этих результатов при увеличении их числа стремится к действительному значению Х измеряемой физической величине т.е. lim(l-xi)=0 Если арифметическая средина образована из свободных относительных ошибок результатов измерений, то она сама не содержит систематической ошибки. Доказывается методом от противного. Из всех функций вида y=C1l1+C2l2+… где С1+С2+…+=1 арифметическая средина. Независимые результаты наблюдений обладают минимальным стандартом. Сумма произведений уклонений Vi=L-li от арифметической средины равна нулю т.е. [pE] или [pv]=0 Сумма произведений квадратов уклонений на соответствующие веса от арифметической средины меньше чем сумма произведений квадратов приближенных поправок на соответствующие веса, получаемым при любой другой функции этих же результатов измерений.
|
Билет №6 1 Плотность распределения Наглядное представление о характеристике распределения в окрестности различных точек дается функцией которая называется плотность распределения вероятности или дифференциальным законом. Плотность распределения случайной величины в точке х называется предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+Δх к длине этого участка Δх Плотность распределения – это производная от функции распределения. Свойства f(x)≥0 Несобственный интеграл от плотности вероятности в бесконечных пределах равен 1. Плотность заключенная под кривой всегда равна 1. Вероятность попадания случайной величины Х на участке от а до b равна интегралу от плотности распределения взятому по этому участку.
2 Свойства арифметической средины. Если результаты измерений свободны от систематических ошибок, то арифметическая средина этих результатов при увеличении их числа стремится к действительному значению Х измеряемой физической величине т.е. lim(l-xi)=0 Если арифметическая средина образована из свободных относительных ошибок результатов измерений, то она сама не содержит систематической ошибки. Доказывается методом от противного. Из всех функций вида y=C1l1+C2l2+… где С1+С2+…+=1 арифметическая средина. Независимые результаты наблюдений обладают минимальным стандартом. Сумма произведений уклонений Vi=L-li от арифметической средины равна нулю т.е. [pE] или [pv]=0 Сумма произведений квадратов уклонений на соответствующие веса от арифметической средины меньше чем сумма произведений квадратов приближенных поправок на соответствующие веса, получаемым при любой другой функции этих же результатов измерений.
|
Билет №6 1 Плотность распределения Наглядное представление о характеристике распределения в окрестности различных точек дается функцией которая называется плотность распределения вероятности или дифференциальным законом. Плотность распределения случайной величины в точке х называется предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+Δх к длине этого участка Δх Плотность распределения – это производная от функции распределения. Свойства f(x)≥0 Несобственный интеграл от плотности вероятности в бесконечных пределах равен 1. Плотность заключенная под кривой всегда равна 1. Вероятность попадания случайной величины Х на участке от а до b равна интегралу от плотности распределения взятому по этому участку.
2 Свойства арифметической средины. Если результаты измерений свободны от систематических ошибок, то арифметическая средина этих результатов при увеличении их числа стремится к действительному значению Х измеряемой физической величине т.е. lim(l-xi)=0 Если арифметическая средина образована из свободных относительных ошибок результатов измерений, то она сама не содержит систематической ошибки. Доказывается методом от противного. Из всех функций вида y=C1l1+C2l2+… где С1+С2+…+=1 арифметическая средина. Независимые результаты наблюдений обладают минимальным стандартом. Сумма произведений уклонений Vi=L-li от арифметической средины равна нулю т.е. [pE] или [pv]=0 Сумма произведений квадратов уклонений на соответствующие веса от арифметической средины меньше чем сумма произведений квадратов приближенных поправок на соответствующие веса, получаемым при любой другой функции этих же результатов измерений.
|
Билет №6 1 Плотность распределения Наглядное представление о характеристике распределения в окрестности различных точек дается функцией которая называется плотность распределения вероятности или дифференциальным законом. Плотность распределения случайной величины в точке х называется предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+Δх к длине этого участка Δх Плотность распределения – это производная от функции распределения. Свойства f(x)≥0 Несобственный интеграл от плотности вероятности в бесконечных пределах равен 1. Плотность заключенная под кривой всегда равна 1. Вероятность попадания случайной величины Х на участке от а до b равна интегралу от плотности распределения взятому по этому участку.
2 Свойства арифметической средины. Если результаты измерений свободны от систематических ошибок, то арифметическая средина этих результатов при увеличении их числа стремится к действительному значению Х измеряемой физической величине т.е. lim(l-xi)=0 Если арифметическая средина образована из свободных относительных ошибок результатов измерений, то она сама не содержит систематической ошибки. Доказывается методом от противного. Из всех функций вида y=C1l1+C2l2+… где С1+С2+…+=1 арифметическая средина. Независимые результаты наблюдений обладают минимальным стандартом. Сумма произведений уклонений Vi=L-li от арифметической средины равна нулю т.е. [pE] или [pv]=0 Сумма произведений квадратов уклонений на соответствующие веса от арифметической средины меньше чем сумма произведений квадратов приближенных поправок на соответствующие веса, получаемым при любой другой функции этих же результатов измерений.
|
Билет 7
1.
Характеристикой центра распределения является математическое ожидание случайной величины.
Обозначается:
![]()
Формула:
![]() - для прерывных
величин.
- для прерывных
величин.
![]() - для непрерывных величин.
- для непрерывных величин.
Доказываеться,
что при неограниченном числе испытаний
среднее арифметическое ![]() =
=![]() , где
, где ![]() -относительная
частота, стремиться по вероятности к
М
-относительная
частота, стремиться по вероятности к
М![]() ,
т.е.
,
т.е. ![]()
Математическое ожидание обладает следующими свойствами:
![]()
![]()


Где, с – постоянная (неслучайная) величина.
2. Вес величина, обратно пропорциональная дисперсии.
![]()
Веса величины относительные .
В случае когда дисперсии неизвестны, вес вычисляют:
![]()
Билет №8
Вопрос 1
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается в русской литературе и (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.
Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
Вопрос 2
Среднее квадратическое отклонение измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднеквадратическое отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
# 9




10.ДОПОЛНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ: АСИММЕТРИЯ И ЭКСЦЕСС Нормированный центральный момент третьего порядка называют асимметрией (скошенностью)
а величина
называется эксцессом и является мерой крутости, т.е. островершинности или плосковершинности кривой. Для кривой плотности нормального закона:Sk=0,E=0. Критериями нормального закона служат неравенства:
где
Значительное отклонение Sk* и E* от нуля, т.е. невыполнение условий , означает отклонение исследуемого распределения случайной величины от нормального.
|
10.Нормальный закон распределения Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности .Нормальный закон распределения также называется законом Гаусса. Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.Можно легко показать, что параметры и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х График плотности нормального распределения называется нормальной кривой или кривой Гаусса.Нормальная кривая обладает следующими свойствами: 1) Функция определена на всей числовой оси. 2) При всех х функция распределения принимает только положительные значения. 3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю. 4) Найдем экстремум функции. Т.к. при y’ > 0 при x < m и y’ < 0 при x > m , то в точке х = т функция имеет максимум, равный . 5) Функция является симметричной относительно прямой х = а, т.к. разность (х – а) входит в функцию плотности распределения в квадрате. 6) Для нахождения точек перегиба графика найдем вторую производную функции плотности. При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб. В этих точках значение функции равно . Построим график функции плотности распределения. Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s= 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.. Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном. При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой:
|
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ОШИБОК
Возможные (конкретные) значения случайной ошибки нельзя предвычислить заранее, можно лишь указать границы, в которых она изменяется. Следовательно, случайная ошибка, как непрерывная случайная величина, может вполне характеризоваться законом распределения вероятностей случайных ошибок. Этот закон, как известно, характеризует объективно существующую связь между возможными значениями случайной величины и вероятностями их появления при многократных испытаниях. Закон распределения случайной ошибки, представленный в виде функции распределения, может быть записан в общем виде
F{A) = P( α<Δ),
где F (Δ) — интегральная функция распределения ошибок Δ.
Таким образом, функцией распределения F (Δ) случайной ошибки α является вероятность того, что случайная ошибка α не превысит величины Δ.
Плотность вероятности распределения случайной ошибки по определению будет равна
![]()
где δΔ — приращение случайной ошибки.

Согласно рис вероятность того, что случайная ошибка α примет значение, заключенное между Δ + δΔ и Δ, может быть представлена в виде
Ρ (А ≤ а ≤ Δ+δΔ) = φ(Δ)·δΔ.
Примем обозначение для φ (Δ)·δΔ, которого и будем придерживаться,
ρ = φ(Δ)·δΔ
Геометрически вероятность ρ в выражении ρ = φ(Δ)·δΔ представляет на рис. площадь заштрихованного элементарного участка при бесконечно малом значении δΔ.
Прежде чем перейти к дальнейшим рассуждениям, приведем без доказательства важную теорему: «Если случайные ошибки удовлетворяют постулату Гаусса, то законом
распределения случайных ошибок является нормальный закот. Постулат Гаусса состоит в свою очередь в том, что наиболее вероятным значением искомой величины является среднее арифметическое из результатов ее повторных наблюдений (если учитывать только случайные ошибки).
Производная
![]() от непрерывной площади F (Δ) согласно
теореме Лейбница—Ньютона, как известно,
есть ордината. Воспользуемся этим
положением для получения формулы для
вычисления ординат кривой распределения
ошибок * (кривой нормаль
от непрерывной площади F (Δ) согласно
теореме Лейбница—Ньютона, как известно,
есть ордината. Воспользуемся этим
положением для получения формулы для
вычисления ординат кривой распределения
ошибок * (кривой нормаль
ного распределения) по заданным значениям Δ.
Обратимся к понятию нормированной случайной ошибки, т. е. примем
![]()
Пусть
![]()
Тогда, принимая во внимание выражение, имеем

Ордината кривой ошибок, как функция значений случайных ошибок Δ, равна
![]()
Обозначим в соответствии с формулами
![]()
Смысл постоянной h, обычно называемой мерой точности, выясним несколько позднее.
С учетом выражения уравнение для ординаты у примет вид
![]()
АСИМЕТРИЯ И ЭКСЦЕСС
Асимметрия
В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой ,
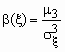
где
m3
- центральный момент третьего порядка,
![]() - среднеквадратичное отклонение.
- среднеквадратичное отклонение.
Эксцесс
Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x , от нормального распределения, является эксцесс.
Эксцесс g случайной величины x определяется равенством .
![]()
У нормального распределения, естественно, g = 0. Если g (x ) > 0, то это означает, что график плотности вероятностей px (x) сильнее “заострен”, чем у нормального распределения, если же g (x ) < 0, то “заостренность” графика px (x) меньше, чем у нормального распределения.
№12 Абсолютные и относительные погрешности
Среднюю квадратическую, среднюю, вероятную, предельну ошибки наз. абсолютными. Её отношение к среднему значению измеренной величины, выраженное дробью с числителем, равным единице, наз. относительной ошибкой. Бывают: средняя квадратическая относительная ош., средняя относительная, вероятная отноительная и предельная относительная.

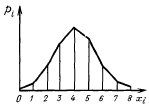 .
Графически в виде так называемого
многоугольникараспределения(графическое
изображение таблицы распределения в
прямоугольных координатах, где по оси
абсцисс откладываются значения Xi
случайной величины X, а по оси ординат
— соответствующие им вероятности pi.
.
Графически в виде так называемого
многоугольникараспределения(графическое
изображение таблицы распределения в
прямоугольных координатах, где по оси
абсцисс откладываются значения Xi
случайной величины X, а по оси ординат
— соответствующие им вероятности pi.