
- •1.Фнп. Основные понятия. Предел и непрерывность фнп.
- •2. Частные производные фнп, их геом. Смысл. Частные производные высших порядков.
- •3.Дифф-сть фнп. Необходимые условия дифф-ти. Достаточное условие дифф-ти.
- •4. Полный дифференциал фнп и его применение в приближенных вычислениях.
- •5. Частные производные сложной функции. Полная производная функции
- •6. Производная от функции, заданной неявно.
- •7.Градиент фнп и его основные свойства.
- •8.Необх. И дост. Условия лок. Экс. Ф-ции 2 переменных.
- •15. Таблица неопределенных интегралов. Метод замены переменной в неопределенном интеграле
- •16. Метод интегрирования по частям. Некоторые типичные интегралы, берущиеся по частям.
- •17. Простейшие рациональные дроби. Метод неопределенных коэффициентов.
- •19. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка.
- •21. Определение и геометрический смысл определенного интеграла.
- •22. Условия интегрируемости функции. Свойства определенного интеграла, его экономический смысл.
- •23. Формула Ньютона-Лейбница.
- •24. Замена переменной и интегрирование по частям в определенном интеграле.
- •25. Приложения определенного интеграла (формулы для площади плоской фигуры и для длины дуги кривой).
- •26. Несобственные интегралы первого рода, их геом. Смысл. Признаки сравнения нес. Интегралов 1-го рода.
- •27. Несобственные интегралы второго рода, их геом. Смысл. Признаки сравнения нес. Интегралов 2 рода
- •29. Повторные интегралы. Вычисление 2-ых интегралов.
- •30. Применение двойных интегралов в геометрии.
- •31.Основные понятия оДу. Т. О сущ-и и ед-ти. Задача Коши. Общий интеграл и общее решение ду. Частные решения. Геом. Смысл ду.
- •32. Ду с разделяющимися и разделен. Переменными.
- •33. Однородные ду первого порядка.
- •34. Линейные ду первого порядка. Метод Бернулли.
- •35. Лоду 2 порядка с постоянными коэффициентами.
- •36. Линейные неоднородные ду второго порядка с постоянными коэффициентами и спец. Правой частью.
- •38. Необходимой условие сходимости числового ряда. Признаки сравнения рядов с неотр. Членами.
32. Ду с разделяющимися и разделен. Переменными.
ДУ вида M (x) dx + N ( y) dy = 0 называют уравнением с разделенными переменными. Общий интеграл уравнения есть ∫М(х)dx + ∫N(y)dy = C. ДУ вида M1 (x) N1 ( y) dх + M2 (x) N2 ( y) dу = 0 называется уравнением с разделяющимися переменными. Уравнение вида y’=f(x) и y’=f(y) сводятся к уравнениям с разделяющими переменными с помощью замены.
33. Однородные ду первого порядка.
Функция f (x, y) называется однородной функцией n-ного измерения относительно переменных x и y , если при любом λ > 0 справедливо тождество f(λx, λy ) = λnf(x,y). Уравнение первого порядка dy/dx=f(x,y) называется однородным относительно x и y , если функция f (x, y) есть
однородная функция нулевого измерения относительно x и y . Уравнение вида M (x, y) dx + N(x, y) dy = 0 будет однородным тогда и только тогда, когда функции M (x, y) и N(x, y) – однородные функции одного и того же измерения; f(x,y) – однородное ур-е нулевого порядка однор-ти, если для любого λ выполняется равенство f(λx, λy)=f(x,y).
34. Линейные ду первого порядка. Метод Бернулли.
ЛДУ первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной:
dy/dx + p(x)y = q(x), где p(x) и q(x) – заданные непрерывные функции от x или постоянные. Для решения исп-тся м-д Бернулли, пояснение на примере:
y’
+
 y
= 3x
– ЛДУ-1; Введем подстановку y(x)=4(x),
где u,v-неизвестные
ф-ции. y’(x)=(u(x)*v(x))’=u’*v+u*v’;
u’*v+u*v’+
*u*v=3x;(1)
v(u’+
*u)+u*v’=3x.
Найдем ф-цию, чтобы выражение в скобках
обращалось в ноль. u’+
*u=0;
u(x)=x-1;
подставим найденное значение в ур-е 1.
*v’=3x;
v(x)=x3+C;
y(x)=
*x3+C.
y
= 3x
– ЛДУ-1; Введем подстановку y(x)=4(x),
где u,v-неизвестные
ф-ции. y’(x)=(u(x)*v(x))’=u’*v+u*v’;
u’*v+u*v’+
*u*v=3x;(1)
v(u’+
*u)+u*v’=3x.
Найдем ф-цию, чтобы выражение в скобках
обращалось в ноль. u’+
*u=0;
u(x)=x-1;
подставим найденное значение в ур-е 1.
*v’=3x;
v(x)=x3+C;
y(x)=
*x3+C.
35. Лоду 2 порядка с постоянными коэффициентами.
y′′ + py′ + qy = 0, где
p, q – действительные числа. Если y1,
y2 – два решения однородного уравнения,
то y1 + y2, C1y1, C2y2 – также решения этого
уравнения. Два решения уравнения
называются линейно независимыми на
отрезке [a,b], если y2/у1↑const
В противном случае они называются
линейно зависимыми ( y2 = λy1). Если y1, y2
два линейно независимых решения
уравнения, то y = C1y1 + C2y2 – его общее
решение. k 2 + pk + q = 0 – характ. уравнение
дискриминанта. Случаи если: Д>0, λ1≠λ2
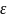 R;
уч.р.(х)
=
R;
уч.р.(х)
=
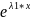 ;
уч.р.2(х)
=
;
уч.р.2(х)
=
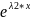 ;
уо.о(х)=С1у1(х)
+ С2у2(х),
уо.о(х)=С1
+ С2
;
если Д=0, то λ1=λ2=λ
ε R;
уч.р.1(х)
=
;
уо.о(х)=С1у1(х)
+ С2у2(х),
уо.о(х)=С1
+ С2
;
если Д=0, то λ1=λ2=λ
ε R;
уч.р.1(х)
=
 ;
уч.р.2(х)
=
;
уч.р.2(х)
=
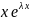 ;
уо.о(х)=
С1
+ С2
;
уо.о(х)=
С1
+ С2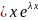 ;
если Д<0, то решение характ. ур-ия
составляют два комплексно-сопряженных
корня; λ1=α
+ iβ;
λ2=
α – iβ,
i=
;
если Д<0, то решение характ. ур-ия
составляют два комплексно-сопряженных
корня; λ1=α
+ iβ;
λ2=
α – iβ,
i=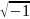 (мнимая
единица); уч.р.1(х)
=
(мнимая
единица); уч.р.1(х)
=
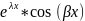 ;
уч.р.2(х)
=
;
уч.р.2(х)
=
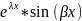 ;
уо.о(х)=
С1
;
уо.о(х)=
С1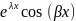 + С2
+ С2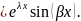 С1,2
ε R.
С1,2
ε R.
36. Линейные неоднородные ду второго порядка с постоянными коэффициентами и спец. Правой частью.
Общее решение ЛДУ y′′ + py′ + qy = f (x) , где p, q – действительные числа, имеет вид у=у’+у*, где y’ – общее решение соответствующего однородного уравнения, y∗ – одно из частных решений неоднородного уравнения.
Для ур-ия справедлива ф-ла: уо.н.= уо.о(х) + уч.н.(х). В различных приложениях правая часть f (x) уравнения во
многих случаях имеет специальный вид. В общем случае:
f (x) = eax (Pr (x)cos bx + Qs (x)sin bx). Частные случаи:
f (x) = Pr (x ) ( a= 0, b=0); f (x) = Pr (x)eax b = 0
37. Опр-ие числовых рядов. Сходящиеся ряды, их св-ва.
a1 + a2 +…+an…=∑an(1) – сумма элементов от 1 до ∞. Это выражение называется числовым рядом или просто рядом, числа a1, a2,…, an,… – членами ряда, an – общим (n -ным) членом ряда. n -ой частичной суммой Sn ряда называется сумма конечного числа n первых членов ряда. Ряд называется сходящимся, если последовательность его частичных сумм сходится к некоторому числу S, которое называется суммой ряда. Если существует конечный предел Sn=S, то ряд называется сходящимся и ∑an=S. Если не существует конечного предела Sn, то ряд называется расходящимся. Cв-ва: ряд и любой его остаток одновременно сходятся или расходятся. Сходимость ряда не нарушится, если произвольным образом изменить конечное число членов ряда. При этом значение суммы сходящегося ряда может измениться. Для того, чтобы ряд сходился необходимо и достаточно, чтобы lim n→∞ rn = 0; Произведением ряда на число С называется ряд: Ca1 + Ca2 +…+ Can…= ∑Can(2); Если ряд (1) сходится и его сумма равна S , то и ряд (2) также сходится и его сумма равна CS. Алгебраической суммой ряда (1) и ряда b1 + b2 +…+bn…=∑bn(3) называется ряд: (a1 +/- b1) + (a2 +/-b2)+…+(an+/-bn)…=∑ (an+/-bn)(4); Если ряды (1) и (3) сходятся, и их суммы равны соответственно Sa и Sb, то и ряд (4) сходится и его сумма равна Sa±Sb . Cходящиеся ряды можно умножать на число, почленно складывать и вычитать.
