
- •Тепломассообмен
- •Теория тепломассообмена
- •Терминология. Общее представление о передачи тепла.
- •Феноменологический
- •Кинетический подход.
- •Если мы возьмём конвективный теплообмен между двумя средами, разделёнными твёрдой перегородкой, то процесс передачи тепла от горячей среды к холодной называется теплопередачей.
- •Фундаментальные соотношения, используемые в качестве замыкающих соотношений в теории тепломассообмена.
- •4) Гипотеза излучения
- •Вывод уравнения теплопроводности.
- •Классическое Уравнение Лапласа
- •Условия однозначности.
- •Решение стационарных задач теплопроводности. Температурное поле и тепловые потоки в плоской стенке
- •В бесконечной плоской стенке поле температур меняется в одном направлении – задача одномерная:
- •Значения температур
- •Температурное поле и плотность теплового потока в цилиндрической стенке.
- •Температурное поле и плотность теплового потока в шаровой (сферической) стенке.
- •Решение задач теплопроводности для граничных условий третьего рода. Плоская стенка. Теплопередача.
- •Вследствие того, что и , отсюда
- •Цилиндрическая стенка. Теплопередача.
- •Температурное поле в пластине (бесконечной плоской стенке) с внутренними источниками тепла.
- •Температурное поле в круговом цилиндре с внутренними источниками тепла.
- •Температурное поле цилиндрической стенки с внутренними источниками тепла.
- •Критический диаметр цилиндрической стенки. Выбор тепловой изоляции.
- •Выбор тепловой изоляции.
- •Интенсификация теплопередачи. В каком-то теплообменном аппарате через единицу поверхности передать наибольшее количество тепла.
- •Повышение интенсивности теплопередачи за счёт оребрения. Теплопроводность стержня (ребра постоянного поперечного сечения).
- •Обозначим:
- •Определение количества тепла, отводимого стержнем конечной длины в окружающую среду.
- •Теплопередача через ребристую плоскую стенку.
- •Коэффициент оребрения:
- •Круглое ребро постоянной толщины. Теплоотвод от круглого ребра.
- •Нестационарные процессы теплопроводности.
- •Охлаждение (нагревание) бесконечной пластины.
- •Задача одномерная, пусть
- •Обозначим:
- •Разложение функции в ряд Фурье
- •В таблицах и монограммах рассчитано для двух точек (в середине пластины
- •Случаи вырождения чисел био.
- •Охлаждение (нагревание) бесконечного цилиндра.
- •Почти уравнение Бесселя
- •Функция является производной
- •Анализ решения.
- •(Порядок малости)
- •Охлаждение (нагревание) тел конечных размеров.
- •Параллелепипед:
- •Цилиндр конечных размеров:
- •Определение количества тепла, отдаваемого телами при охлаждении.
- •Бесконечная пластина:
- •Бесконечный цилиндр:
- •Смотри справочные данные. Поиск сводится к средней температуре. Регулярный режим охлаждения (нагревания) тел.
- •Эта стадия охлаждения или нагревания когда описывается одним членом ряда называется регулярным режим охлаждения, нагревания тел.
- •Теоремы Кондратьева для регулярного режима.
- •Конвективный теплообмен.
- •Пути решения задач
- •Вывод дифференциальных уравнений конвективного теплообмена Уравнение неразрывности.
- •Уравнение сохранения количества движения
- •Уравнение энергии
- •Использование методов анализа размерности в задачах тепломассообмена.
- •Пример использования -теоремы.
- •Теорема Гухмана о подобных явлениях.
- •Система уравнений в приближения пограничного слоя.
- •Расчёт теплоотдачи при продольном обтекании пластины.
- •Результаты численного решения.
- •Решение задачи теплообмена на пластине.
- •Теплообмен при продольном обтекании пластины и турбулентном режиме течения. Аналогия Рейнольдса.
- •Расчёт интенсивности теплообмена при вынужденном стабилизированном течении жидкости в трубе. Особенности движения жидкости на начальном участке.
- •Принципиальные приближения:
- •Профили скорости при стабилизированном течении жидкости в трубе.
- •Расчёт интенсивности теплообмена при турбулентном течении жидкости в трубе.
- •Расчёт интенсивности теплообмена в шероховатых трубах.
- •Каналы некруглого поперечного сечения.
- •Изогнутые трубы (змеевики).
- •Кольцевые каналы.
- •Расчёт интенсивности теплообмена при поперечном обтекании трубного пучка.
Температурное поле и плотность теплового потока в шаровой (сферической) стенке.
![]()
З


![]() аданы:
аданы:
![]() Так
же заданы граничные условия первого
рода:
Так
же заданы граничные условия первого
рода:
![]()
Здесь не существует торцевого эффекта, задача является одномерной:
![]()
Уравнение теплопроводности для нашего случая:
![]()
Проинтегрируем:
![]()
Рассмотрим два геометрических тела:
Шар – может выделять тепло, если есть внутренние источники тепла:
![]()
![]()
![]()
Шаровая (сферическая стенка)
![]()

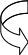 -
текущий радиус
-
текущий радиус
Домножим
на
![]() :
:
![]() (*)
(*)
В сферической стенке, полня передаваемая (переносимая) энергия не зависит от радиуса и является величиной постоянной.
Умножим
выражение (*) на
![]() и
проинтегрируем:
и
проинтегрируем:
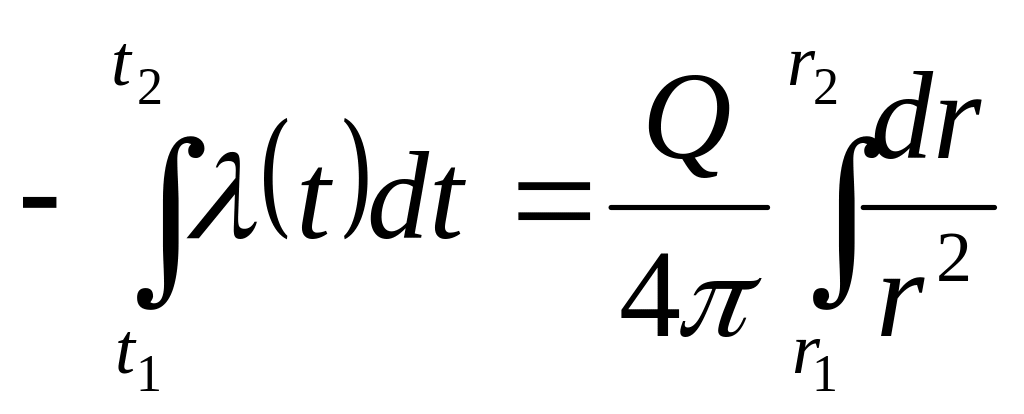 ;
умножим
на
;
умножим
на
![]()

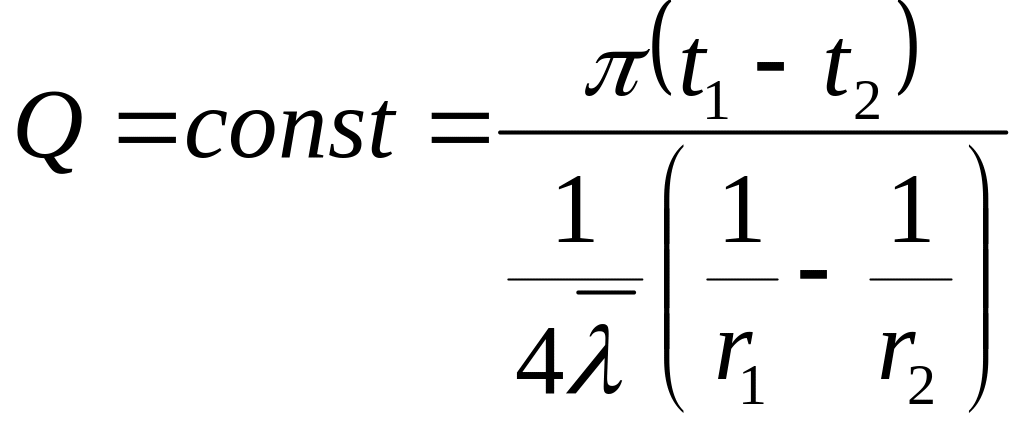
(*)
термическое сопротивление
шарового слоя.
Для многослойной сферической стенки:
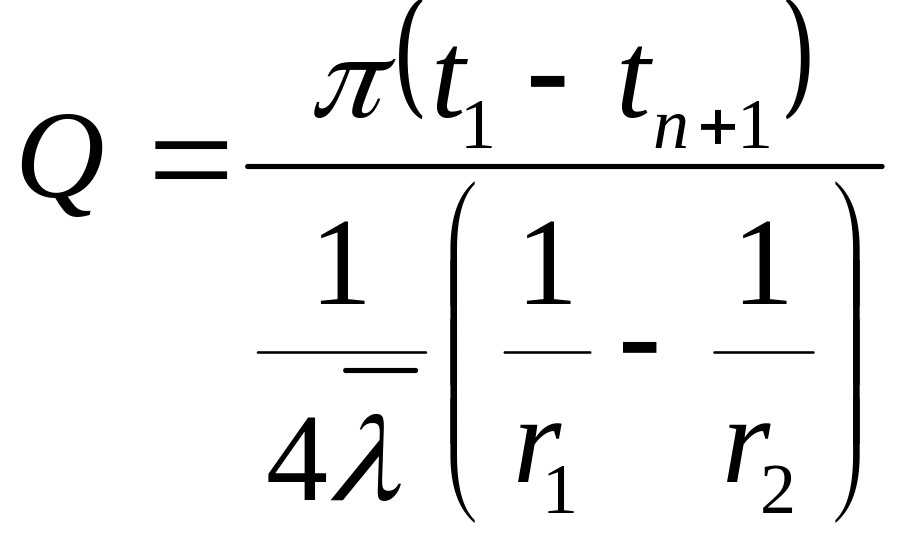
Температурное поле:
![]()
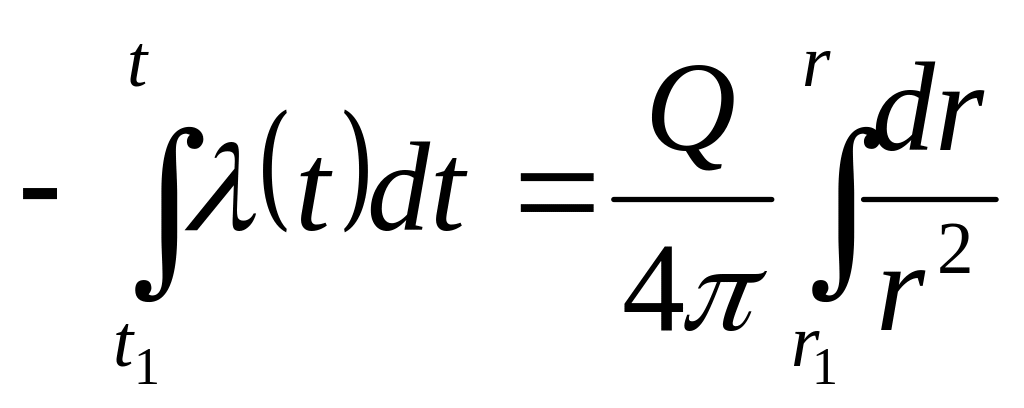
Рассмотрим простейший вариант: пусть
![]()

![]() ;
подставим
значение для Q
из выражения (*):
;
подставим
значение для Q
из выражения (*):
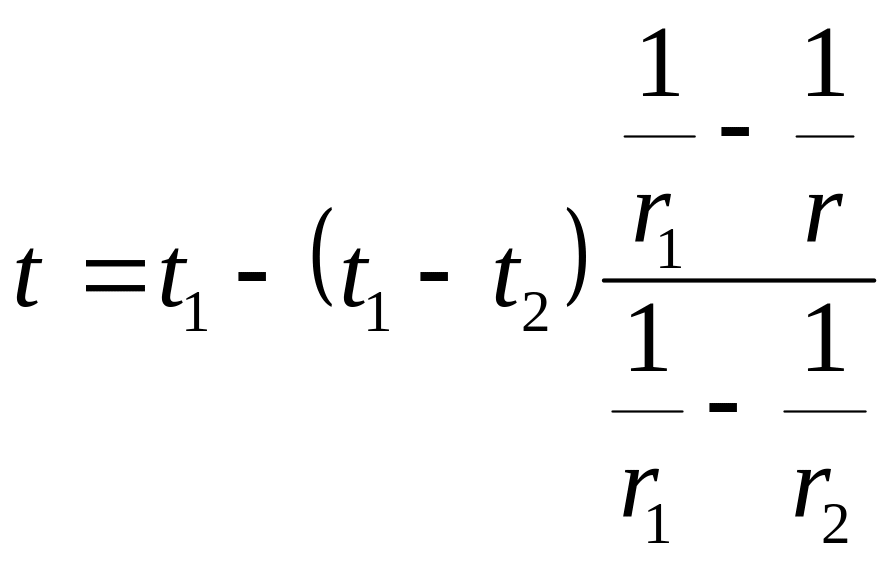
Это температурное поле для шарового слоя (гиперболическая функция).
Решение задач теплопроводности для граничных условий третьего рода. Плоская стенка. Теплопередача.


![]()
![]()
![]()
![]()
![]()
Заданы:
![]()
![]() Значение
коэффициентов теплоотдачи
Значение
коэффициентов теплоотдачи
Среда представляется текучей
К![]() роме
этого известно значение температур
жидкости:
роме
этого известно значение температур
жидкости:
Вследствие того, что и , отсюда
Граничные условия третьего рода заключаются в том, что нам известна плотность теплового потока:
![]() -
граничные условия левой части стенки.
-
граничные условия левой части стенки.
Рассмотрим связь между плотностью теплового потока и температурой стенки:
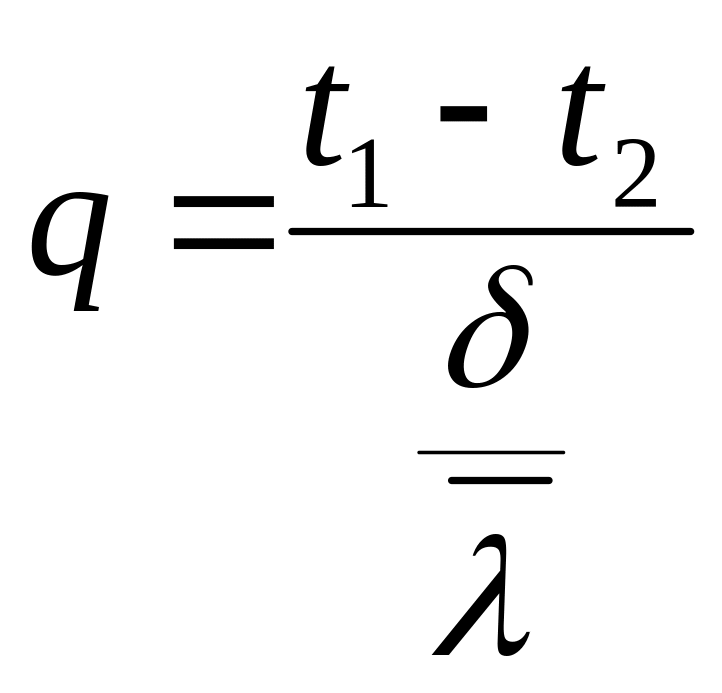
(см.
решение ранее)
![]() - граничные
условия для правой стенки.
- граничные
условия для правой стенки.
П![]() ереписывая
наши выражения, получим:
ереписывая
наши выражения, получим:
С![]() ложив,
получим:
Мы получили выражения для
плотности теплового потока при
теплопередаче
ложив,
получим:
Мы получили выражения для
плотности теплового потока при
теплопередаче
![]() -
термическое сопротивление теплопередаче
через плоскую
стенку.
-
термическое сопротивление теплопередаче
через плоскую
стенку.
![]()
![]() -
коэффициент
теплопередачи через плоскую стенку
-
коэффициент
теплопередачи через плоскую стенку
![]()
- термическое сопротивление материала плоской стенки.
![]()
- термические сопротивления теплоотдаче.
Многослойная плоская стенка. Теплопередача.
Записывая выражение для разности температур между слоями и по гипотезе Ньютона -Рихмана, мы получим следующий результат:
![]()
![]() -
термическое сопротивление теплопередаче
через многослойную плоскую стенку.
-
термическое сопротивление теплопередаче
через многослойную плоскую стенку.
![]() -
коэффициент теплопередачи через
многослойную плоскую стенку.
-
коэффициент теплопередачи через
многослойную плоскую стенку.
Цилиндрическая стенка. Теплопередача.


![]()
![]()
![]()
![]()
Заданы:
![]()
Нам известно, что :
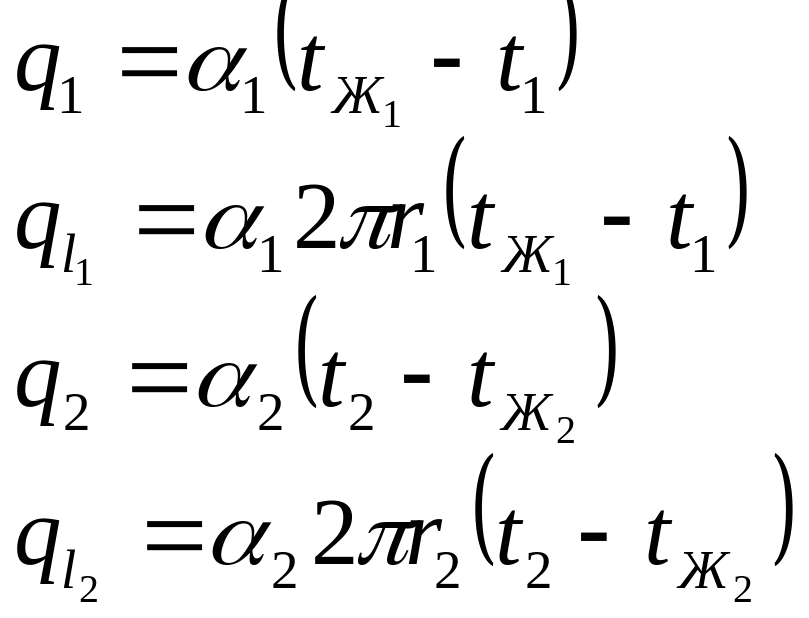
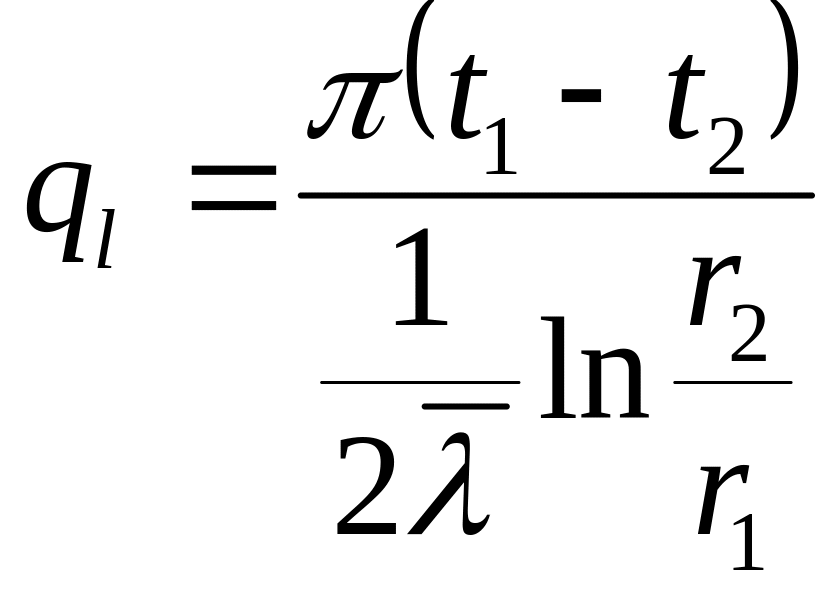 (см.
решение ранее)
(см.
решение ранее)
Переписывая наши выражения для разности температур и сложив их, получим:
![]()
где:
![]() -
термическое
сопротивление
теплопередачи через цилиндрическую
стенку
-
термическое
сопротивление
теплопередачи через цилиндрическую
стенку
![]() -
термическое сопротивление теплопроводности
стенки.
-
термическое сопротивление теплопроводности
стенки.
![]()
- линейное термическое сопротивление теплоотдаче через цилиндрическую стенку
Многослойная цилиндрическая стенка. Теплопередача.
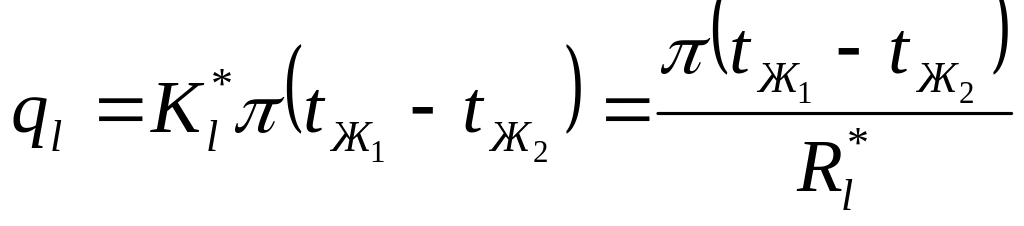
где:
![]() -
линейное
термическое сопротивление теплопередаче
для многослойной цилиндрической стенки.
-
линейное
термическое сопротивление теплопередаче
для многослойной цилиндрической стенки.
![]() -
линейный коэффициент теплопередачи
через многослойную цилиндрическую
стенку.
-
линейный коэффициент теплопередачи
через многослойную цилиндрическую
стенку.
Запишем связь между плотностями теплового потока, учитывая что в цилиндрической стенке:
![]()
где
![]() -
любой текущий радиус:
-
любой текущий радиус:![]()
![]() -
передаваемое через поверхность тепло.
-
передаваемое через поверхность тепло.
![]() В нашем случае:
В нашем случае:
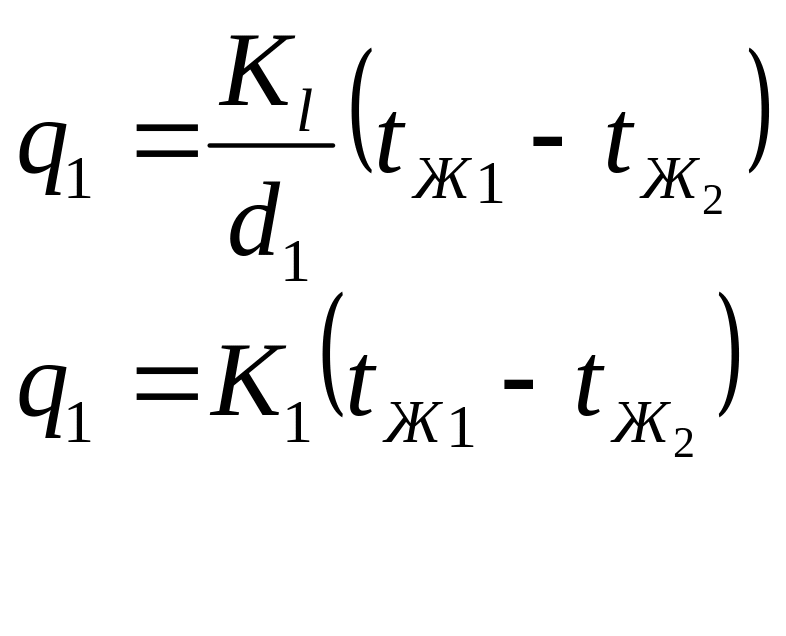
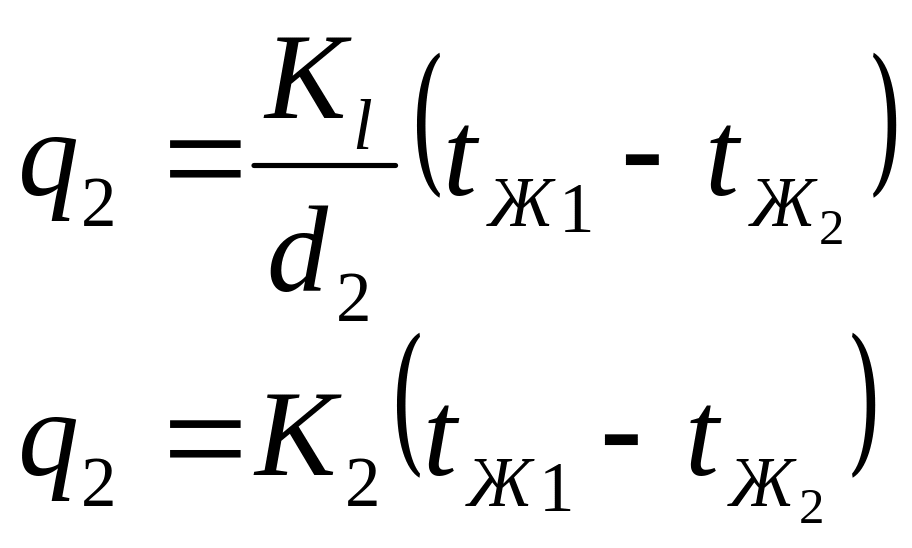
Плотность теплового потока на единицу поверхности с ростом радиуса уменьшается.
![]() -
коэффициенты теплопередачи, отнесённые
к поверхности 1 или 2.
-
коэффициенты теплопередачи, отнесённые
к поверхности 1 или 2.
Существует понятие тонких цилиндрических стенок.
![]() Возьмём
Возьмём
![]() где
где
Если
![]() можно
с достаточной точностью представить
как первый член разложения, то это тонкая
стенка.
можно
с достаточной точностью представить
как первый член разложения, то это тонкая
стенка.
Для тонких стенок выражение для полного количества тепла. передаваемого через цилиндрическую стенку может быть записано в следующем виде.
![]() (*)
(*)
Причём К рассчитывается как для плоской стенки а диаметр dx берётся по стороне с наименьшим коэффициентом теплоотдачи. Если коэффициенты теплоотдачи близки друг другу то расчётный диаметр является средним арифметическим:
![]()

Докажем это:
Учитывая, что для
тонкой цилиндрической стенки
![]() ,
запишем:
,
запишем:
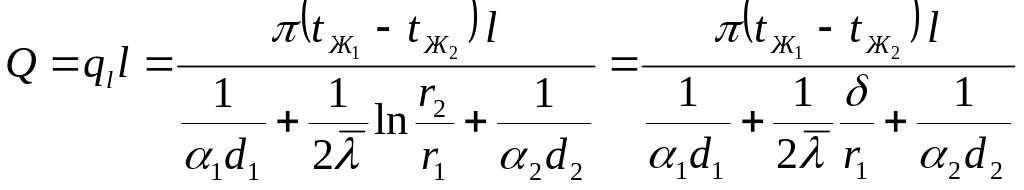
Если стенка тонкая,
то мы можем предположить, что
![]() ,
то есть:
,
то есть:
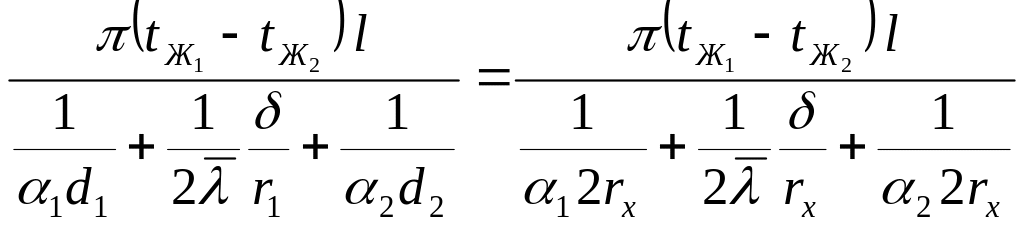
Преобразуем знаменатель,
вынося за скобки
![]() :
:
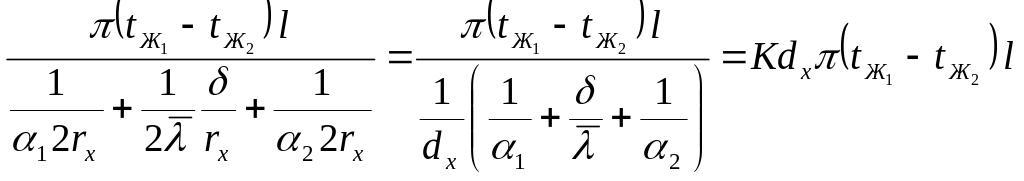
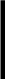
Справедливость выражения (*) для цилиндрической тонкой стенки доказана.
